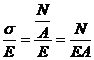ELEMENTE SOLICITATE LA INTINDERE SI COMPRESIUNE CENTRICA
1.1. INTINDEREA
SI COMPRESIUNEA CENTRICA. DEFINITIE; EXEMPLE
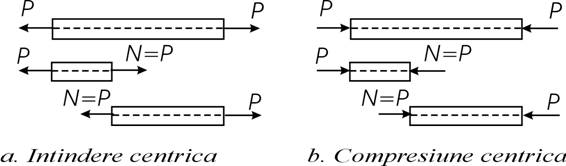
Intinderea/compresiunea centrica este solicitarea
simpla in prezenta careia, in sectiunea transversala,
interactiunea este exprimata printr-o pereche de forte axiale
(fig.3.1).

fig.3.1.
O pereche de forte echilibrate aplicate pe o
bara dreapta de-a lungul axului ei genereaza intre punctele de
aplicatii intindere/compresiune centrica (fig.3.2). Forta
axiala N are intensitatatae P a fiecaruia din cele doua
forte exterioare
Fig.
3.2.
In practica, intinderea/compresiunea centrica
este solicitarea caracteristica barelor grinzilor cu zabrele (si
in general sistemelor alcatuite din bare drepte articulate la capete,
incarcate cu forte in punctele de articulare), numai sub forma
de intindere, ea este proprie firelor (drepte, poligonale sau curbe).
1.2. REZISTENTA
BARELOR INTINSE/COMPRIMATE CENTRIC
1.2.1. Eforturi
unitare pe sectiunea transversala
Studiul geometric (privind modul de deformare). Pe
suprafetele laterale ale unei bare drepte cu sectiune
dreptunghiulara se traseaza un sistem de linii longitudinale
(paralele cu axa) si transversale (perpendiculare pe axa). In regim
de solicitare (fig.3.3) liniile transversale se departeaza /aproape
(prin translatii) ramanand
drepte, paralele intre ele si normale pe cele longitudinale.
Fig.
3.3.
Observatia corespunde ipotezei Bernoulli
(sectiuni transversale plane si normale pe axa raman plane
si normale tot timpul deformarii), confirmand-o (cu putin pe
suprafata - vizibila - a barei)
Cu privire la cele doua tipuri de deformatii
(liniare si unghiulare) se constata
- lipsa deformatiilor unghiulare ( = 0) caci unghiurile retelei nu se
modifica
- prezenta unor deformatii liniare egale in
toate fibrele longitudinale ale barei (Dl = const., deci e = const.).
Studiul fizici consemneaza conditia de
elasticitate liniara (legea lui Hooke) acceptata in Rezistenta
materialelor.
Sinteza studiu geometrica - studiu fizic.
Daca g = 0, rezulta t = 0. Daca e = const., rezulta
= const. Pe sectiunea transversala, interactiunea
punctuala este exprimata prin eforturi unitare normale t egale (uniform distribuite) (fig.3.4).
Fig.
3.4.
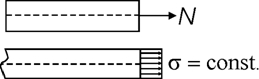
Studiul static. Efortul sectional N si
sistemul de eforturi unitare sunt masura aceleasi interactiuni.
Studiul static consemneaza echivalenta dintre cele doua moduri
de exprimare ale ei:
N = 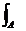 s dA
s dA
Sinteza studiu geometric - studiu static. Intrucat s = const.
N = s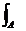 dA = tA,
dA = tA,
de
unde:
= 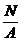 (3.1)
(3.1)
Marimea efortului unitar depinde de doi
parametri:
- forta axiala N, parametrul global al
interactiunii din sectiune, masura solicitarii
- aria A, parametrul geometriei sectiunii
transversale.
I.2.2. Proiectarea
de rezistenta a sectiunii barelor intinse/comprimate centric
1.2.2.1. Conditii de rezistenta.
Verificare; dimensionare, capacitate portanta. Conditia de
rezistenta impusa de metoda rezistentelor admisibile (1.1)
devine
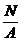 sa
sa
Relatia
contine trei parametri; ei corespund celor trei factori care apar an
procesul celor trei factori care apar in procesul proiectarii
sectiunii:
-
solicitarea, exprimata prin forta axiala N;
-
materialul, exprimat prin rezistenta sa admisibila ta
-
geometria suprafetei sectiunii transversale, exprimata prin aria
A.
Dupa
felul in care acestia intervin (ca parametrii cunoscuti sau
necunoscuti), proiectaread imbraca trei aspecte: verificarea,
dimensionarea si determinarea capacitatii portante a
sectiunii.
Cele
trei aspecte ale proiectarii sunt prezentate sintetic in tabelul 3.1
si comentate in continuare.
Tabelul 3.1.
|
Parametri
cunoscuti
|
Parametri necunoscuti
|
Relatia de calcul
|
|
Verificare
|
N, sa, A
|
|
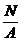 sa sa
|
|
Dimensionare
|
N, sa
|
Aria necesara
Anec
|
Anec = 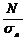
|
|
Capacitate portanta
|
sa, A
|
Forta capabila
Ncap
|
Ncap = saA
|
In problemele de dimensionare, dupa stabilirea
ariei necesare Anec, dimensiunile sectiunii (carora le va
corespunde aria efectiva Aef) se aleg astfel, incat, indiferent de forma
ei , Aef Anec.
Capacitatea portanta a unei sectiuni se
masoara prin forta axiala - numita forta
capabila, Ncap - corespunzatoare unor eforturi unitare
egale cu rezistenta admisibila. Rezistenta barei este
asigurata daca efortul axial N corespunzator solicitarii
(determinat in functie de incarcari) nu depaseste
efortul capabil N Ncap.
1.2.2.2. Observatie privind proiectarea barelor
comprimate.
Barele comprimate se pot distruge mai inainte cu
eforturile unitare (determinate cu raport intre forta axiala si
aria sectiunii transversale) sa atinga limita de rupere sau de
curgere a materialului, prin fenomenul numit flambaj*. In principiu, pericolul
flambajului este cu atat mai mare cu cat barele sunt mai svelte. Numai barele
robuste (cu lungimea redusa si sectiuni transversale desvoltate)
pot fi proiectate la compresiune in conditiile analizate in capitolul de
fata.
1.2.3. Concentrari de eforturi
In sectiuni transversale foarte apropiate de
punctul de aplicatie a fortei exterioare axiale (fig.3.8) ipoteza lui
Bernoulli (a sectiunilor plane.) este infirmata de experiment. Fibrele
longitudinale din preajma axei barei, cu deformatii longitudinale mai
mari, vor fi mai puternic solicitate;
*) Flambajul va fi analizat pe
larg in unul din capitolele urmatoare ale cursului.
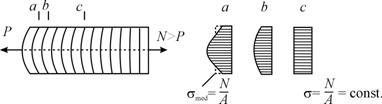
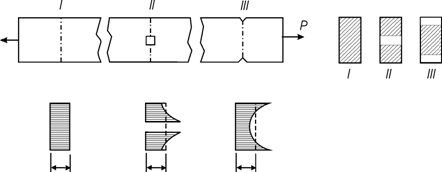
Fig.3.8.
fig.3.8 prezinta
distributia eforturilor unitare s in trei sectiuni (a, b, c) aflate la distante
diferite de punctul de aplicatii a fortei exterioare.
In sectiuni transversale suficient de
departate de punctul de aplicatie a fortelor exterioare,
distributia in sectiune a eforturilor unitare nu este
influentata de modul de aplicare a acestor forte (principiului
Saint-Venant).
Neuniformitatile in distributia
eforturilor unitare pe sectiunea transversala apar si la
variatii .... ale formei sectiunii (gauri, crestaturi etc.)
(fig.3.9).
Concentratiile de eforturi din sectiunile
slabite de gauri sau crestaturi au consecinte diferite la
materialele casante si ductile.
La materialele casante bara se rupe brusc cand "varful"
eforturilor atinge tr (deci la o valoare a
efortului mediu mult mai mica decat tr (fig.3.10). La materialele ductile (cu curgere, sau cu
deformatii plastice mari) ruperea este un proces indelungat, care se
sfarseste chiar dupa ce, treptat, pe masura ce
creste solicitarea, toate eforturile unitare din sectiune ating
rezistenta de curgere; distributia eforturilor unitare in cateva faze
premergatoare ruperii unei bare alcatuite din material ductil este
prezentata in fig.3.11.
fig.3.10
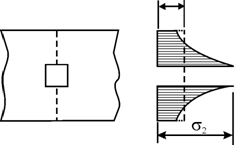
fig.3.10
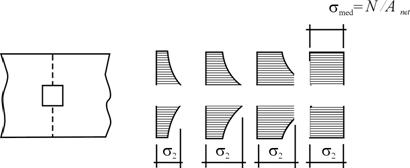
fig. 3.11
1.3.
DEFORMATIILE BARELOR INTINSE/COMPRIMATE CETRIC
1.3.1.
Calculul deformatiilor
Intre deformatii si eforturi exista
legatura liniara exprimata de legea lui Hook s = Ee; de aici se deduce expresia formatiilor specifice
liniare e
e = 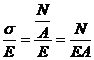
Deformatia specifica liniara e este proportionala cu solicitarea (N) si
invers proportionala cu factorul de rigiditate la intindere
/compresiune (produsul EA); acesta, la randul lui, depinde de doua
categorii de parametri: modulul de elasticitate E (care exprima
rigiditatea materialului) si aria suprafetei sectiunii
transversale A (care exprima rigiditatea sectiunii).
Cum e reprezinta deformatia unitatii de
lungime, deformatia intregii unitati de lungime, deformatia
intregii bare (alungirea sau scurtarea Dl) e proportionala cu lungimea l:
Dl = el (3.3)
Dl = 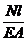 (3.4)
(3.4)
1.3.2. Efectul static al variatiilor de
temperatura in bare
O bara libera, cu lungimea l, supusa
unei variatii de temperatura Dto se dilata/contracta
(alungeste/scurteaya) cu cantiatea.
Dlt = Dto a l (3.5)
unde a este coeficientul de dilatatie termica al
materialului; pentru otel,
a = 1,2 . 10-5
Aplicatie. La o variatie de temperatura
de 30o, o bara de otel de 8 m lungime se
alungeste/scurteaza cu
Dlt = 30 . 1,2 . 10-5 . 8000 mm =
2,88 mm
Daca dilatatia/contractia barei este
impiedicata de legaturile acesteia in sistem, in bara apar
eforturi tt de compresiune/intindere corespunzatoare
alungirii/scurtarii blocate (ca si cum eforturi axiale de compresiune
N ar constrange bara dilatata cu cantitatea Dlt sa revina la pozitia
initiala printr-o scurtare DlN egala
Dlt = Dl N;
Dto . a . l = 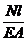 ,
,
de unde
st = 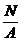 = Dt . a . E (3.6)
= Dt . a . E (3.6)
Aplicatie. Pentru bara din exemplul precedent,
blocarea deformatiilor de dilatare/contractie genereaya eforturi
unitare care consuma mai mult de jumatate din reyistenta
admisibila a materialului:
st = 30 . 1,2
. 10-5 . 2,1 . 106 = 755 Kgf/cm2
De remarcat ca in expresia eforturilor unitare
(3.6) nu intervine geometria barei (nici aria sectiunii transversale, nici lungimea). Eforturile nu
pot fi moderate prin dimensionare, ci printr-o conformare de
ansamblu a structurii care sa
permita deformatii libere.
In sistemul static determinate (cu numar minim de
legaturi) deformatiile de dilatare/contractie se produc liber
(fig.3.12.a), deci fara consecinte asupra starii de efort
din bare.
Legaturile suplimentare ale sistemelor static
nedeterminate ingradesc libertatea
de deformare, generand in bare eforturi (fig.3.12.b).
 Podurile
metalice sunt totdeauna structuri simplu rezemate (cu un reazem fix si
altul mobil), cu posibilitatea de dilatare sau contractii neblocata
in lungul axului podului.
Podurile
metalice sunt totdeauna structuri simplu rezemate (cu un reazem fix si
altul mobil), cu posibilitatea de dilatare sau contractii neblocata
in lungul axului podului.
fig. 3.12