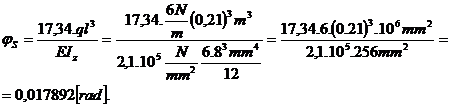Integrarea analitica a ecuatiei diferentiale
a fibrei medii deformate in cazul grinzilor de sectiune constanta si executate din
acelas material adica ( E1
= E2 =E3 = . =En ) cu mai multe campuri de variatie a momentului
incovoietor. Procedeul lui Clebsch sau al identificarii constantelor de
integrare.
Acest procedeu reduce
numarul constantelor de integrare la doua C si D , pe cand la metoda
analitica se introducea pentru fiecare regiune cate doua constante de
integrare , ca atare pentru o bara cu trei sau mai multe regiuni, metoda
analitica devine destul de complicata .
Procedeul Clebsch
impune anumite restrictii :
originea
de masura a absciselor se fixeaza intotdeauna la unul din
capetele barei, indiferent daca este reazem sau capat de
consola.
originea
odata aleasa ramane
neschimbata pe tot timpul rezolvarii problemei, pozitionarea
fortelor ( sarcinilor) si a sectiunilor curente se face numai
fata de aceasta origine.
toti termenii expresiei momentului incovoietor din
regiunea
( campul ) precedenta
trebuie lasati neschimbati ca forma in functia
momentului incovoietor al regiunii urmatoare a grinzii.
toti
termenii expresiei momentului
incovoietor care apar in regiunea urmatoare, incepand cu regiunea a doua,
trebuie sa contina binomul ( xi - aj ) .
integrarea
ecuatiei diferentiale, trebuie
facuta fara a se
desface
parantezele binomului ( xi - aj )n .
6) tronsoanele barei sa
fie din acelasi material si sectiunea transversala sa fie constanta pe toata lungimea barei. De aici reiese
particularitatea acestui procedeu.
Cand exista de rezolvat integrala de forma:  ; se
face schimbarea de variabila
; se
face schimbarea de variabila 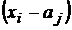 = t ; se
diferentiaza d
= t ; se
diferentiaza d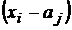 = dt ;
= dt ; 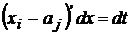 ; dx =
dt ;
; dx =
dt ;  =
=  ; unde t =
; unde t = 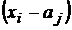 , si deci
, si deci  =
=  .
.
Sa
demonstram existenta a numai
doua constante de integrare C si D , pentru o grinda
incarcata ca in figura, acest caz particular duce prin
inductia matematica la rezolvarea oricarui tip de
incarcare. Aplicam metoda analitica de calcul a sagetilor
si a rotirilor sectiunilor transversale,
pentru fiecare regiune in parte si ne folosim de faptul ca
functia axei de simetrie deformata trebuie sa fie continua
si derivabila pe tot domeniul maxim de definitie.
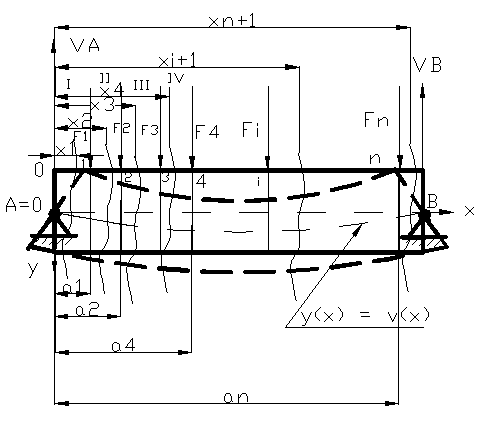
Figura 1
Regiunea intai
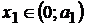 ;
;  ; ; ecuatia fibrei medii
; ; ecuatia fibrei medii
deformate va fi : 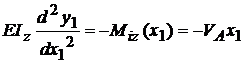 ,
,
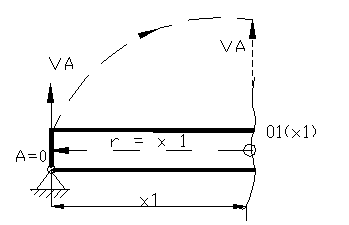
Figura 2
prin integrari succesive se obtin, urmatoarele
expresii;  ;
;
Pentru regiunea a II-a
 ;
; 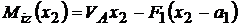 ; ecuatia fibrei
medii deformate va fi :
; ecuatia fibrei
medii deformate va fi : 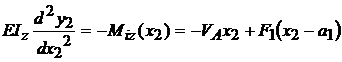
prin integrari
succesive se obtin, urmatoarele expresii:
 ; ( 2 )
; ( 2 )
Punem conditiile de continuitate si derivabilitate ale
functiilor ce exprima sagetile si rotirile
sectiunilor transversale , in sectiunea ( 1 ) [functia y(x) = v(x) sa
fie continua si derivabila]. Deci  ; la fel si
; la fel si
 De unde rezulta
:
De unde rezulta
:

de aici implica C1 = C2 si D1 = D2 .
S-a precizat ca acest procedeu este limitat la barele executate
din acelas material si nu variaza dimensiunile sectiunilor
transversale.
Regiunea a III-a
 ;
;  ; ; ecuatia fibrei medii deformate va fi :
; ; ecuatia fibrei medii deformate va fi :

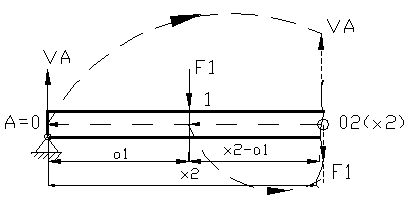
Figura 3
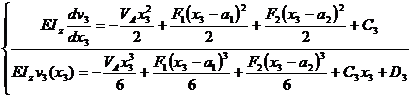
Punem
conditiile de continuitate si derivabilitate ale functiilor ce
exprima sagetile si rotirile sectiunilor transversale
, in sectiunea ( 2 ) [functia y(x) = v(x) trebuie sa fie continua
si derivabila].
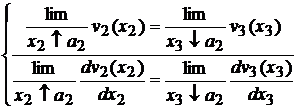 ;
; 

Figura 4
de aici implica C1 = C2
= C3 si D1 =
D2 = D3.
Prin inductie
matematica rezulta ca : C1 = C2
= C3 = . = Cn = C
si D1 = D2 = D3.= . =
Dn = D , unde
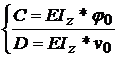 ; v0
este sageata in origine, iar φ0 rotirea in origine a sectiunii
transversale.
; v0
este sageata in origine, iar φ0 rotirea in origine a sectiunii
transversale.
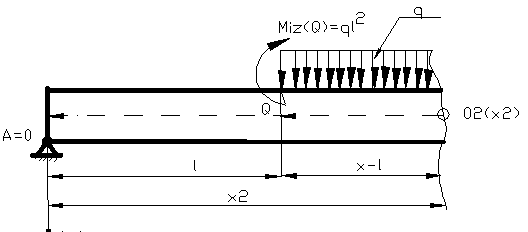
Problema nr.5
Sa se calculeze
sagetile si rotirile sectiunilor transversale Q si S
pentru bara din figura 5, stiind ca :
E = 2,1 . 105 N/mm2
; q = 6 N / m ; l =
0,21 m , sectiunea transversala fiind dreptunghiulara cu b = 6 mm
si h = 8 mm .
Rezolvare:
Calculam
sagetile si rotirile sectiunilor transversale Q si
S cu ajutorul procedeului Clebsch pentru
grinda din figura 5, alegem ca origine , articulatia din (A) .
Se scrie ecuatia momentului generalizator
din ultima regiune (B-S), apoi se calculeaza expresia functiilor pentru
sageti si rotiri tot cu elemente generalizatoare . 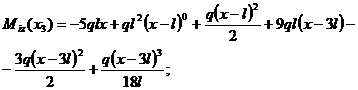 cu ;
cu ; 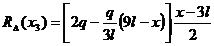 ; incarcarea trapezoidala s-a desfacut intr-un
triunghi si intr-un dreptunghi. Forta
rezultanta pentru triunghi .
; incarcarea trapezoidala s-a desfacut intr-un
triunghi si intr-un dreptunghi. Forta
rezultanta pentru triunghi .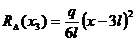 , forta
rezultanta pentru dreptunghi Rdreptunghi(x3)=q(x3)(x3-3l), pentru trapezul dreptunghic variabil din
figura 6, s-a aplicat principiul
suprapunerii efectelor. Deasemenea pentru a avea in expresia momentului
incovoietor termenii binomiali
, forta
rezultanta pentru dreptunghi Rdreptunghi(x3)=q(x3)(x3-3l), pentru trapezul dreptunghic variabil din
figura 6, s-a aplicat principiul
suprapunerii efectelor. Deasemenea pentru a avea in expresia momentului
incovoietor termenii binomiali
( xi - aj
)n s- a pus la momentul
incovoietor concentrat Miz (
Q ) = ql2 bratul
( x - l )0 [ orice numar la puterea zero este egal cu
unu ], apoi s-a prelungit functia de incarcare q(x) = q din regiunea a II-a [ sus si jos pe
aceeasi lungime ( x-3l )] ca
urmare a aplicarii principiului suprapunerii efectelor.
Functia de
incarcare pentru regiunea a III-a ( fiind triunghiulara ) se afla din
teorema lui Thales :
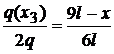 ; 6l - x + 3l = 9l - x ;
; 6l - x + 3l = 9l - x ; 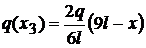 ;
;
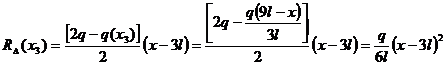
Rdreptunghi=
 ; cand se
; cand se
exprima momentele
incovoietoare ale sarcinii distribuite data de incarcarea
trapezoidala fata de sectiunea ( x ) , se obtin defalcat momentul
incovoietor pentru incarcarea triunghiulara si respectiv
momentul incovoietor pentru incarcarea dreptunghiulara.

Figura 6

Figura 5

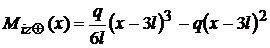 , momentul incovoietor pentru
, momentul incovoietor pentru
incarcarea dreptunghiulara din regiunea a III-a ,
 ; momentul incovoietor pentru incarcarea triunghiulara din regiunea a III-a.
; momentul incovoietor pentru incarcarea triunghiulara din regiunea a III-a.
Momentului
generalizator din ultima regiune:

Figura 7
 Aplicam ecuatia
fibrei medii deformate:
Aplicam ecuatia
fibrei medii deformate:  ;
;

prin integrari succesive se obtin, urmatoarele
expresii;

S-au obtinut expresiile sagetilor si a rotirilor
sectiunilor transversale in forme generalizatoare, se afla
constantele C si D din conditiile de sprijin ( de reazem ) ale barei.
O prima conditie este :
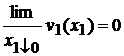 ; la fel si
; la fel si 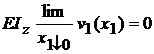 ; in regiunea
intai ,
; in regiunea
intai , 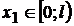

Figura 8
 ; pentru expresia momentului incovoietor
; pentru expresia momentului incovoietor
din regiunea intai, se ia
din expresia momentului incovoietor generalizator numai primul termen , la fel
se tine cont si in expresiile sagetilor sau rotirilor.

 ; D = 0 . A doua conditie de reazem va fi:
; D = 0 . A doua conditie de reazem va fi:  .Conditiile de
reazem ( de sprijin ) sunt cuprinse in conditiile de continuitate si
derivabilitate ale functiei fibrei
medii deformate.
.Conditiile de
reazem ( de sprijin ) sunt cuprinse in conditiile de continuitate si
derivabilitate ale functiei fibrei
medii deformate.
In
regiunea a II-a ,  ;
;
 Figura
9
Figura
9
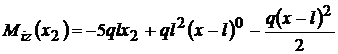 ; pentru expresia
; pentru expresia
momentului incovoietor din regiunea a II-a, se ia din momentului
incovoietor generalizator numai termenii care dau moment incovoietor pentru
regiunea a II-a , in mod analog se procedeaza la expresiile
sagetilor si a rotirilor sectiunilor tranversale , se iau
numai primii trei termeni la care se adauga contributia lui C si
D .
 ;
;
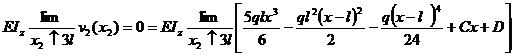 ;
;
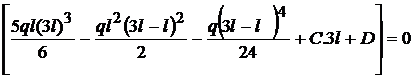 ;
;
C = - 19,83 ql3 .
Avand determinate constantele de integrare C si D , s-au
obtinut
functiile
sagetilor si rotirilor sectiunilor transversale penru orice
punct de pe bara .
 ;
;
Acum se
calculeaza sageata si rotirea in punctul Q , care se afla
in
regiunea intai deci se ia numai primul termen la care se adauga
cotributia C si D :

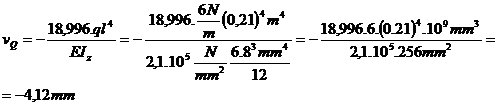
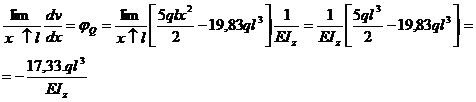
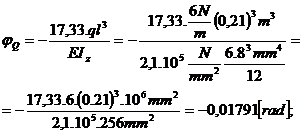
vQ = -
4,12 mm.
Pentru
sectiunea din punctul S se iau expresiile generalizatoare ,
deoarece (S ) cade in ultima regiune pentru care s-a facut
momentul incovoietor generalizator.
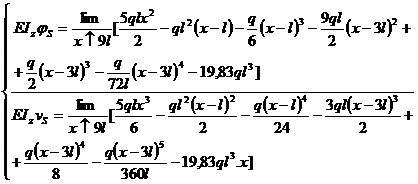

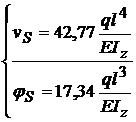 ;
;

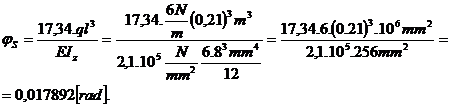


 ; unde t =
; unde t =  .
.
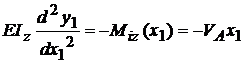 ,
,
 ;
;  ;
; 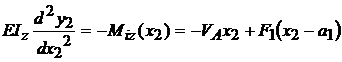
 ; ( 2 )
; ( 2 )  ; la fel si
; la fel si De unde rezulta
:
De unde rezulta
: 


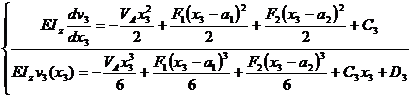
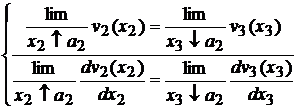 ;
; 

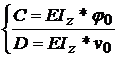 ; v0
este sageata in origine, iar φ0 rotirea in origine a sectiunii
transversale.
; v0
este sageata in origine, iar φ0 rotirea in origine a sectiunii
transversale.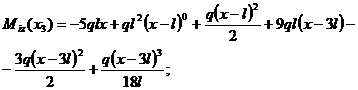 cu ;
cu ; 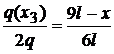 ; 6l - x + 3l = 9l - x ;
; 6l - x + 3l = 9l - x ; 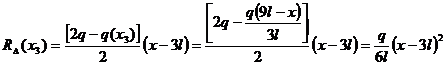




 ;
;

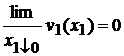 ; la fel si
; la fel si 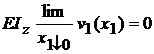 ; in regiunea
intai ,
; in regiunea
intai , 

 ; D = 0 . A doua conditie de reazem va fi:
; D = 0 . A doua conditie de reazem va fi:  .Conditiile de
reazem ( de sprijin ) sunt cuprinse in conditiile de continuitate si
derivabilitate ale functiei fibrei
medii deformate.
.Conditiile de
reazem ( de sprijin ) sunt cuprinse in conditiile de continuitate si
derivabilitate ale functiei fibrei
medii deformate. Figura
9
Figura
9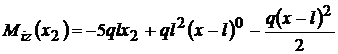 ; pentru expresia
; pentru expresia 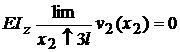 ;
; 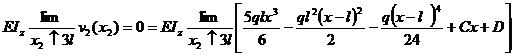 ;
; 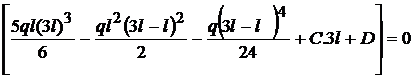 ;
;  ;
;
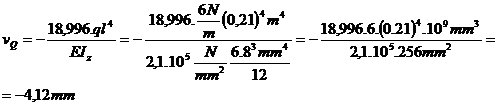
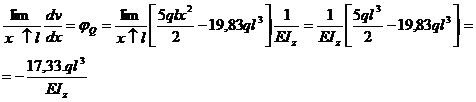
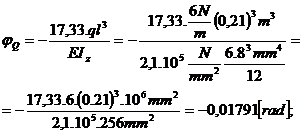
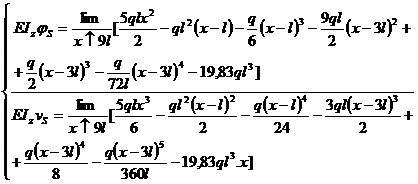

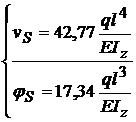 ;
;