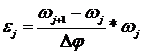MECANISME
TEMA
La mecanismul,
reprezentat schematic in figura se cunosc: 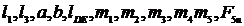 (forta rezistenta utila la elementul 5
(forta rezistenta utila la elementul 5 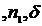 (gradul de neregularitate a miscarii,admis)si
modul de distributie a maselor barelor pe lungimea lor .
(gradul de neregularitate a miscarii,admis)si
modul de distributie a maselor barelor pe lungimea lor .
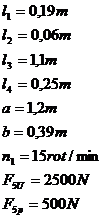
Se cer:
Configuratia grafica a mecanismului pentru 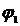
 si numai pozitiile
punctelor
si numai pozitiile
punctelor 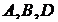 din
din 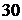 in
in 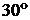 (
(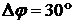 ).
).
Rezolvarea analitica a configuratiei pentru cele 12 pozitii.
Rezolvarea , prin metoda grafo-analitica
a vitezelor si acceleratiilor punctelor principale, pentru
pozitia desenata a mecanismului.
Rezolvarea prin
metoda analitica a campului de viteze pentru cele 12 pozitii
5. Calculul momentului de inertie al masei reduse la elementul 1 .
6. Calculul momentului redus la elementul 1.
Calculul energiei cinetice in functie de pozitiile mecanismului.
Alegera motorului electric si a reductorului de viteza.
Calculul momentului de inertie al volantului .
Analiza miscarii in faza de pornire in sarcina.
Reprezentarile grafice: 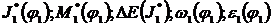 .
.
1.REPREZENTAREA LA
SCARA A SCHEMEI MECANISMULUI
Pentru desenarea schemei mecanismului se admite scara de reprezentare
pentru lungimi , 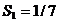 , asfel ca
, asfel ca
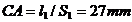
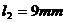
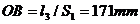
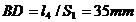
Se traseaza cercul
de raza OA(traiectoria puntului A)si se imparte in 12 parti
comform pasului unghiular dat.
Din punctul C se duc
semidrepte prin punctele de divizare pana la intersectia cu arcul de
cerc cu raza CB (traiectoria punctului B)si rezulta cele 12
pozitii ale punctului B.
2.REZOLVAREA
ANALITICA A CONFIGURATIEI PENTRU CELE 12 POZITII ALE
MECANISMULUI
Se considera sistemul de axe cu originea in articulatia din
O. Proiectiile pe axe ale barelor mecanismului determina coordonatele
punctelor A si B.
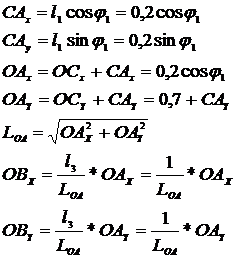
Rezultatele calculelor sunt sistematizate in tabelul 1.
3.REZOLVAREA GRAFICA A CAMPULUI DE VITEZE SI ACCELERATII
PENTRU POZITIA DESENATA
3.1 REZOLVAREA VITEZELOR
Se incepe cu calculul vitezei punctului A de pe
elementul conducator aflat in miscare de rotatie
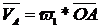
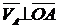
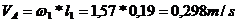
Deoarece vectorul 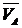 urmeaza a fi
reprezentat grafic este necesar sa se aleaga o scara de
reperzentare pentru viteza.
urmeaza a fi
reprezentat grafic este necesar sa se aleaga o scara de
reperzentare pentru viteza.
Pentru 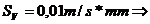
 modulul vectorului viteza
modulul vectorului viteza
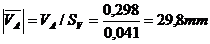
Punctul A apartine
si patinei 2 iar instantaneu are un corespondent si pe elementul 3,ce
se va nota cu 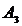 .
.
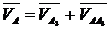
Acesta ecuatie
vectoriala are doua necunoscute modulele
celor doua necunoscute.
Directiile lor sunt
cunoscute :
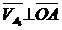 si
si 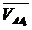 ||
|| 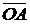 astfel ca
ecuatia se rezolva grafic.
astfel ca
ecuatia se rezolva grafic.
Se reprezinta
vectorul 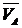 ,si apoi prin origine si extremitati se
duc dreptele
,si apoi prin origine si extremitati se
duc dreptele 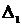 ||
||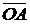 si
si 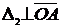
Se masoara pe
desen  si
si 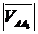
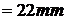 .
.
Se calculeaza
scalarii acestor viteze
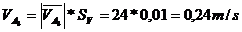
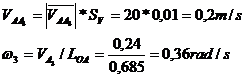
Se calculeaza viteza punctului B aflat in miscare de rotatie, cu centrul
im O .
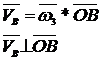

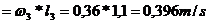
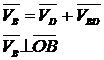
 ||
||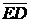

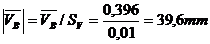
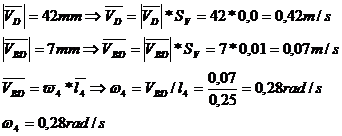
3.2 REZOLVAREA
ACCELERATIILOR
Se rezolva ca la
campul de viteze. Se incepe cu punctul A apartinand manivelei
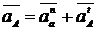
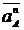 ||
|| 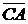 Sensul vectorului
acceleratie normala este spre centrul de rotatie.
Sensul vectorului
acceleratie normala este spre centrul de rotatie.
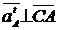

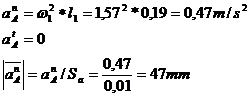
Fata de
sistemul de referinta mobil (transportorul 3) acceleratia are
componentele
de transport, relativa si complementara.
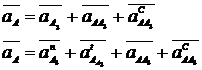
Ecuatia
vectoriala are doua necunoscute modulele
vectorilor 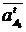 si
si 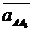
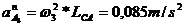 ;
;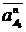 ||
|| 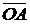
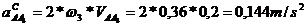
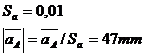

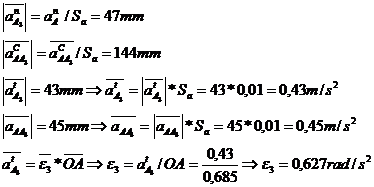
In mod similar se
procedeaza in punctul B
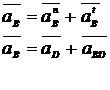

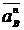 ||
||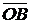
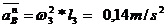
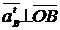
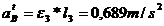
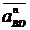 ||
||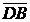
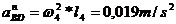
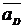 ||
||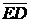
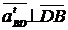
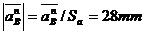

4.REZOLVAREA VITEZELOR
ANALITIC
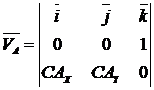
De unde se deduc
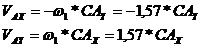
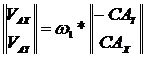
Se scriu relatiile
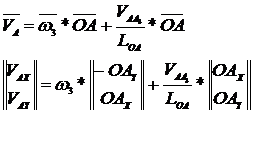
Rezolvand sistemul
se obtin
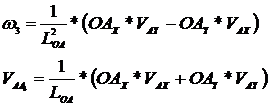
Relatia
devine
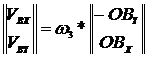
De unde se deduc:
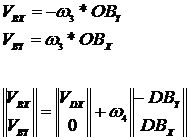
Relatia
devine
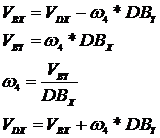
Rezultatele
calculelor se dau in tabelul 2
5.MOMENTUL DE
INERTIE AL MASEI REDUSE LA ELEMENTUL CONDUCATOR
Relatia
generala de calcul este
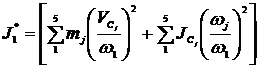
care ,scrisa dezvoltat pentru mecanismul dat devine
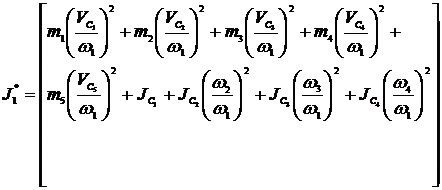
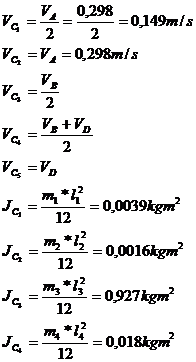
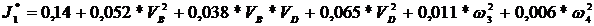
6.CALCULUL MOMENTULUI REDUS LA ELEMENTUL CONDUCATOR
Relatia
generala de calcul este 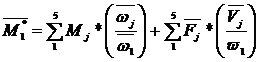
In cazul nostru
relatia devine
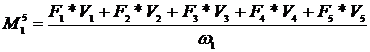
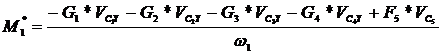
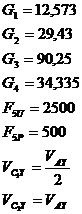
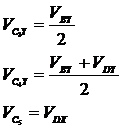
Relatia devine :
 -pentru cursa activa
-pentru cursa activa
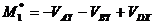
-pentru cursa pasiva
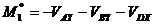
|
Poz
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
7.CALCULUL ENERGIEI
CINETICE IN FUNCTIE DE POZITIA MECANISMULUI
Energia cinetica a
angrenajului format din motor, transmisie si mecanismul dat este
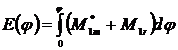
In care  este momentul motor redus la axul manivelei, iar
este momentul motor redus la axul manivelei, iar 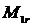 este momentul rezistent calculat la axul manivelei.Cum
este momentul rezistent calculat la axul manivelei.Cum 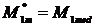 si
si 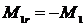 rezulta :
rezulta :
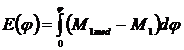
Calculul integralelor se
face grafic :

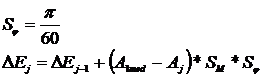
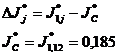
8.
ALEGEREA MOTORULUI ELECTRIC SI A REDUCTORULUI DE
VITEZA
Puterea necesara la axul manivelei este
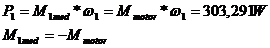
Randamentul mecanic al reductorului se calculeaza cu relatia :
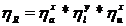
unde:
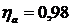 -randamentul angrenarii;
-randamentul angrenarii;
 -randamentul lagarelor unui arbore;
-randamentul lagarelor unui arbore;
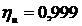 -randamentul barbotarii uleiului in baie;
-randamentul barbotarii uleiului in baie;
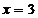 -numarul de trepte;
-numarul de trepte;
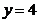 -numarul arborilor .
-numarul arborilor .
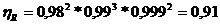
S-a ales motorul AIM1325-8 , cu caracteristicile urmatoare:
Tipul
motorului
|
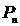
|
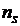
|
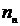
|
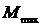
|
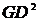
|

|
|
AIM
1325-8
|
|
|
|
|
|
|
Raportul de transmitere al miscarii necesar la reductor se
calculeaza cu relatia:
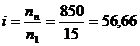
Pentru raportul de transmitere calculat se foloseste un reductor cu 5
trepte de roti dintate pentru care 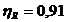 .
.
Puterea necesara la axul motorului va fi :
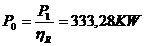 .
.
Viteza unghiulara de sincronism :
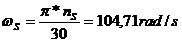 .
.
Viteza unghiulara nominala:
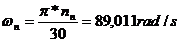 .
.
Alunecarea specifica nominala:
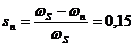 .
.
Momentul nominal al motorului:
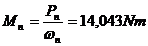 .
.
Coeficientul de suprasarcina:
 .
.
Alunecarea specifica critica :
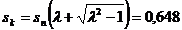
9.CALCULUL MOMENTULUI DE INERTIE AL VOLANTULUI
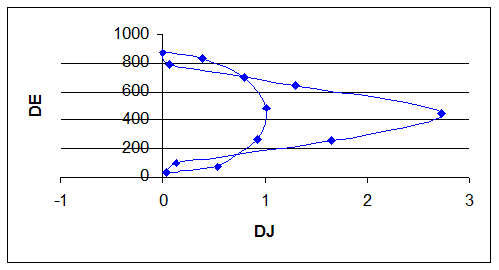
Calculul momentului de inertie al volantului se face cu o metoda
grafo-analitica.Pentru aceasta se traseaza gafic folosind rezultatele
din tabelul 12. Se aleg scari de reprezentare pentru energia cinetica
si pentru momentul de inertie al masei reduse.
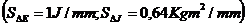
Se calculeza apoi:
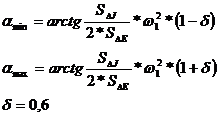
Rezulta:
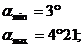
Se duc tangente inclinate cu aceste unghiuri si la intersectia cu
axa energiei rezulta punctele A, B si deci AB=82mm. Momentul de
inertie necesar oentru volant va fi:
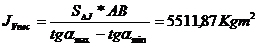
Momentul de inertie al masei volantului va fi:
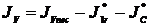
Considerand numai efectul de inertie al masei rotorului motorului
electric :
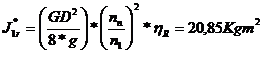
rezulta:
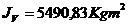 .
.
Considerandu-se masa concentrata in obada se poate estima
greutatea si gabaritul volantului. Formula de calcul pentru raza de
inertie a masei este:
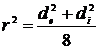
rezulta legatura dintre momentul de inertie al masei
volantului si dimensiunile obadei:
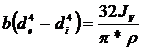 .
.
In care  7870 este densitatea
materialului.
7870 este densitatea
materialului.
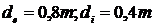 si rezulta
si rezulta 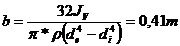 .
.
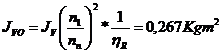 .
.
Se recalculeaza dimensiunule volantului pentru 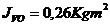 . Se accepta urmatoarele dimensiuni:
. Se accepta urmatoarele dimensiuni: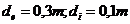 si rezulta :
si rezulta :
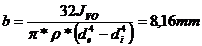 .
.
Se calculeaza raza de inertie al masei volantului :
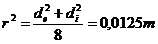 .
.
10.ANALIZA MISCARII IN FAZA DE PORNIRE IN SARCINA
Pornirea agregatelor se face in mod obisnuit in gol adica
fara actiunea sarcinii rezistente utile. Cu agregatul in
miscare se cupleaza apoi si dispozitivul ce solicita util
mecanismul. In aceasta situatie pot fi analizate doua faze de
miscare tranzitorii: faza pornirii in gol si apoi faza de cuplare a
sistemului ce solicita util mecanismul.
Se considera ca agregatul se porneste in plina
sarcina.
Momentul de inertie al maselor redus, total este:
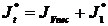 .
.
Valorile calculate se inregistreaza in tabelul 12.
Momentul motor, in functie de alunecarea de la motoarele asincrone cu
rotorul in scurtcircuit, redus la axul manivelei este:
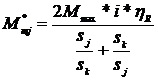 .
.
Pentru j=0 se considera 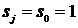 si relatia devine:
si relatia devine:
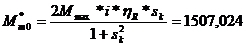 .
.
Viteza unghiulara pentru primul pas:
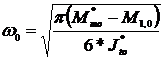
In care :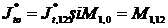 . Se obtine
. Se obtine 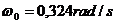 .
.
Viteza unghiulara urmatoare pozitiei anterioare este:
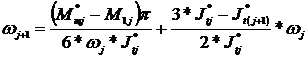 .
.
Alunecarea specifica corespunzatoare va fi:
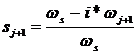 .
.
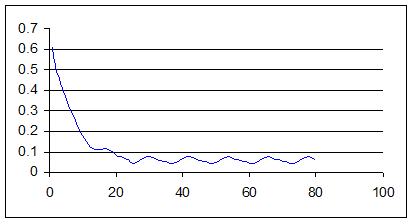
Se calculeza apoi: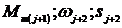 si asa mai departe pana cand se obtin
valori ale vitezei unghiulare cu marimi in jurul celei nominale.
si asa mai departe pana cand se obtin
valori ale vitezei unghiulare cu marimi in jurul celei nominale.
Calculele se sistematizeaza in tabelul 13.
|
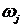
|
|
Poz
|
Rot I
|
Rot
II
|
Rot
III
|
Rot
IV
|
Rot V
|
Rot
VI
|
Rot
VII
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
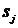
|
|
Poz
|
Rot.I
|
Rot.II
|
Rot.III
|
Rot.IV
|
Rot.V
|
Rot.VI
|
Rot.
VII
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
| | | | | | | | | | |
|
|
|
Poz
|
Rot.I
|
Rot.II
|
Rot.III
|
Rot.IV
|
Rot.V
|
Rot.VI
|
Rot.VII
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|

|
|
Poz.
|
Rot.I
|
Rot.II
|
Rot.III
|
Rot.IV
|
Rot.
V
|
Rot.VI
|
Rot.VII
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
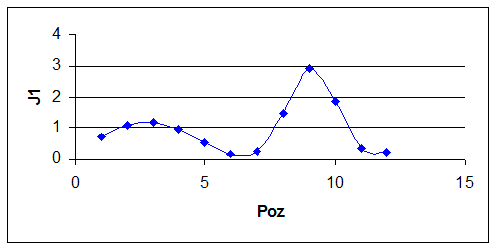
Cunoscand valorile numerice pentru viteza unghiulara se poate calcula
si variatia acceleratiei unghiulare:
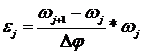


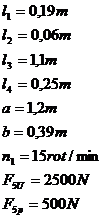
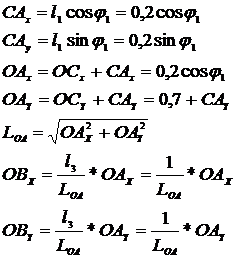
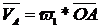
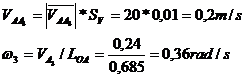
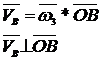
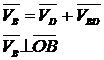
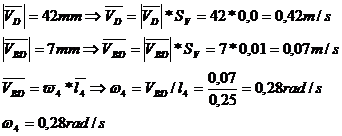
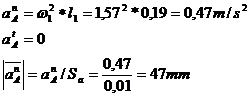
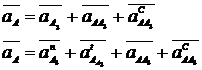
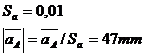
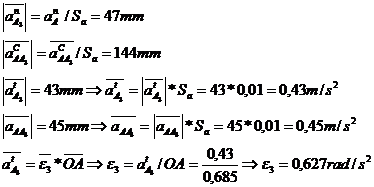
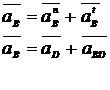

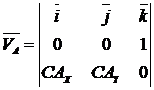
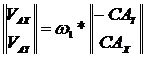
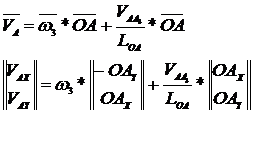
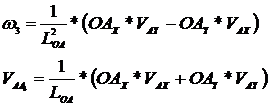
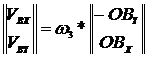
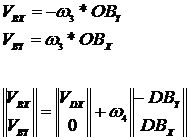
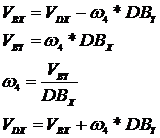
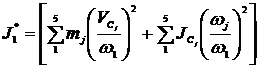
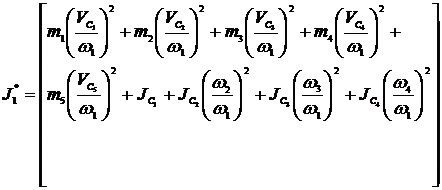
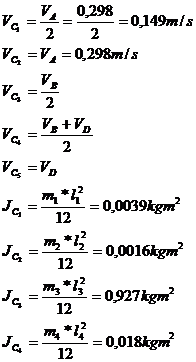
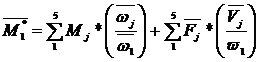
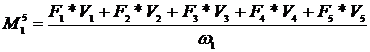
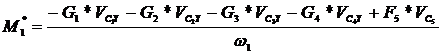
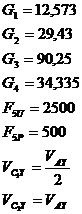

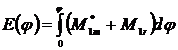
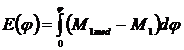

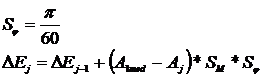
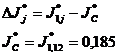
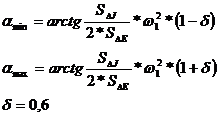
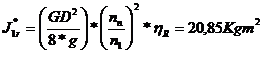
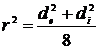
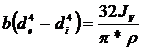 .
.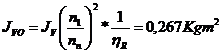 .
.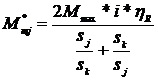 .
.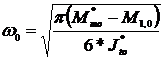
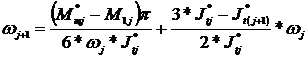 .
.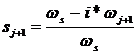 .
.