|
|
MATEMATICA
SI ARHITECTURA
Arhitectura este o arta specifica spatiului caci construŽieste in spatiu
diferite volume. Ea nu a fost de la inceput o arta, ci a devenit, caci primii
oameni care au avut ideea sa-si sape un adapost sub pamant sau sa-si
conŽstruiasca o colita nu s-au gandit sa creeze o opera artistica. Abia mai
tarziu, privind acele constructii ale sale, omul a cautat sa le faca in asa
fel ca ele sa fie placute la vedere si, astfel, arhitectura a devenit si o
arta, alaturi de o meserie, aceea de a construi ceva care are un scop
utilitar. Marele arhitect francez de origine elvetiana Le Corbussier (1887
-1965) afirma ca "arhitectura este o arta, un fenomen emotional, in afara
Problemelor de constructie si dincolo de ele'. Constructia este pentru a
tine, spunea el, dar arhitecŽtura pentru a emotiona !
|
Admiram si azi, dar totodata ne infioara piramidele egiptene, care prin
masivitatea lor indestructibila infrunta mileniile. lnfatisarea lor vorbeste
despre geometrie si totusi nu vom sti nicioŽdata cum a fost posibila
construirea lor fiindca in nici o scriere ramasa de atunci nu se pomeneste
nimic despre aceasta realizare. Cind a fost inaltata marea piramida a lui
Kheops, ea era cel mai inalt monument de pe Pamant si a fost considerata ca una
dintre cele 7 minuni ale lumii : este ca un munte inalt de 150 m care se
zareste de la o departare de 40 km ! Aceasta piramida are ca baza un patrat,
iar fetele sale laterale sint triunghiuri isoscele.
Din scrierile ramase de la Herodot se stie ca impresia de armonie si
maretie pe care o imprastie in jurul ei nu este intamplatoare, ci a fost
calculata cu precizie. Anume, el a aratat ca a aflat de la arhitectii egipteni,
care pe acea vreme erau, si preoti, ca piramida lui Kheops a fost construita in
asa fel ca aria triunghiului isoscel care formeaza o fata laterala sa fie egala
cu aria patratului care ar avea ca latura inaltimea piramidei. Ca sa stabilim
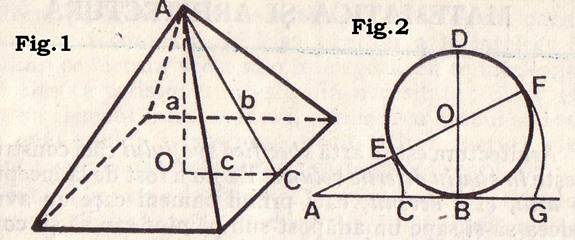
aceasta relatie, sa construim piramida patrata cu virful in A (fig. 1), si
inaltime AO. Ducem apotema AC a unei fete laterale, asa ca triunghiul
dreptunghic AOC este semiprofilul meridian al piramidei. Notam cu a lungimea
inaltimei piramidei, cu b a apoŽtemei, si cu 2c a laturii patratului de la baza
ei. Din cele ce a destainuit preotul egiptean rezulta ca : (1) b*c=a^2, adica
aria triunghiului isoscel lateral (b*c) este egala cu aria patratului de latura
a. Dar relatia (1) se poate scrie sub forma de proportie . Aceasta arata ca inaltimea pirmaidei este
medie proportionala intre doua dintre laturile triunghiului meridian al
piramidei : b si c. Insa acest triunghi AOC, fiind dreptunghic, rezulta : (2)
b^2=b*c+c^2. Impartind prin c^2 relatia devine: (3) (b/c)^2-b/c-1=0. Iata o
formula foarte interesanta care, dupa cum am descoperit, leaga doua dintre
laturile piramidei.
Ca sa o cercetam ma indeaproape, vom pune problema sub o forma mai
generala, anume: dandu-se un segment de dreapta AB (fig.2) sa-l impartim in
doua parti neegale AC si CB (AC>CB), astfel ca segmental intreg catre cel
mai mare catre cel mai mic. Aceasta impartire a unui segment a fost numita de
Euclid "impartirea in medie si extrema ratie", iar acum se numeste taietura de
aur. Desi numirea de taietura sau sectiune de aur nu a fost data de geometrii
greci, ei au cunoscut impresia de armonie ce se degaja din folosirea
segmentelor neegale, al caror raport se afla in taietura de aur si au folosit
asemenea segmente in operele de sculptura sau arhitectura, mai ales in secolul
lui Pericle. Aceasta impartire se poate executa cu rigla si compasul astfel:
Desenam segmental dat AB=a si ridicam perpendiculara BD din B pe AB, astfel ca
BD=AB=a. Se construieste cercul O tangent in B la AB, avand BD ca diametru si O
ca centru. Dupa cum se stie din teorema puterii unui punct fata de un cerc,
secanta AO, determina pe cerc punctele E si F, astfel ca AB^2= AE*AF.
Construind segmentele AE =AC si AG =AF, relatia stabilita mai sus se poate
scrie sub forma : AB^2= AC*AG sau (4) AB/AC=AG/AB=(AC+AB)/AB=AC/CB adica
AB/AC=AC/CB (5).
In rezumat, constructia segmentului AC se face ducand cercul tangent in B
de raza egala cu AB, si apoi transferand pe AB, segmentul AE taiat de secanta
AO pe cerc. Sa stabilim acum relatia care leaga segŽmentele AB =a de AC =b ~i
CB =c. Din (5) avem , dar a=b+c si
deci sau : , si inmultind cu , rezulta (b/c)^2- b/c-1=0 adica relatia (3).
|
Am ajuns astfel la concluzia ca cele doua laturi din triunghiul meridian
al piramidei lui Kheops reprezinta doua segmente care sant in taietacra de
aur.
|
|
Acest triunghi meridian AOC a capatat numirea de triunŽghiul egipitean si
se caracterizeaza prin faptul ca ipoteŽnuza lui este in taietura de aur cu cea
mai mica dintre catete. Dealtfel, in piramida lui Kheops mai exista si alte
dimensiuni care au fost alese in asa fel ca sa fie in taietura de aur. De pilda
in camera regelui, care se afla in interiorul piramidei si se ajunge la ea
printr-un coridor ce comunica cu exteriorul printr-o deschiŽdere ce se afla la
vreo 14 m deasupra solului. Aceasta camera este in forma de paralelipiped,
avind ca baza un patrat dublu (adica un dreptunghi cu una din laturi de doua
ori mai mare decat cealalta), iar ca inaltime jumatate din diagonala acestui
dreptunghi: . Dar ce legatura exista
intre si taietura de aur? Nimic mai
simplu decat de stabilit acest lucru. Sa reluam relatia (3) sis a notam
raportul (litera greceasca , initiala numelui sculptorului Fidias), asa
cum se obisnuieste acum. Avem
deci ecuatia . De aici rezulta valoarea
Cine sic and s-a descoperit ca impresia pe care o lasa o figura in care
segmentele din care este compusa ea ar avea alte dimensiuni, nu se stie.
|

|
Numirea de tatieturi de aur a aparut in timpul Renasterii si a fost data
de Leonardo da Vinci, care era un admirator
|
al acestei proportii, si care a ilustrat o carte despre acest subiect,
compusa de prietenul sau, matematcianul Luca Pacioli (1445-1514 ?), carte care
a fost intitulata "Proportia divina'. Cert este ca impartirea unui segment
in doua segmente neegale care sa verifice egalitatea despre care am vorbit a
atras atentia arhitectilor cu milenii inaintea erei noastre fara ca sa i se
atribuie vreo denumire particulara. Una dintre cele mai de seama calitati ale
arhitectilor greci a fost tocmai aceea ca au 'tradus intuitia lor estetica prin
anumite rapoarte numerice ca, de pilda, taietura de aur dintre segmentele
prezente in cladirile lor. Prin fnfatisarea lor, templele grecesti se impart in
trei ordine : doric, ionic ,si corintic. Fiecare dintre aceste ordine au la baza
proportii diferite in care s-au executat coloanele, frontoanele etc. De pilda,
in templul lui Poseidon, zeul marilor, reprezentand ordinul doric, care se pare
ca a fost construit prin secolul al VI-lea f.e.n., se simte forta plina de
maretie, de severitate ,si de viata pe care o degaja aspectul coloanelor sale.
Avand o inaltime de aproape sase ori cit diametrul, coloanele lui fac impresia
unor copaci crescuti din pamint. Baza lor nu are nici un fel de ornament, iar
capitelul are forma unui colac pe care este asezata lespedea de piatra ce
sprijina acoperisul in panta a templului. Acesta incadreaza frontonul in forma
de triunghi isoscel. Prin masivitatea lui el aminteste ceva din influenta
egipteana, dar sentimentul pe care-l trezeste in severitatea lui infatisarea
acestui templu este de inviorare si optimism. Cu totul alta este impresia ce o
inspira templul Victoriei de pe Acropola Atenei, apartinand ordinului ionic.
Coloanele lui sunt mai zvelte si mai elegante decat acelea ale templului lui
Poseidon. Raportul dintre inaltimea si diametrul lor este de 9 la 1, adica
inaltimea unei coloane este de opt sau de noua ori cat diametrul, si, prin
aceasta, ele par mai pline de vioiciune. Dealtfel aceste coloane nu mai rasar
direct din pamant, ci stau pe un piedestal format din trei sau chiar patru
inele cilindrice suprapuse, iar capitelul-coloanelor este impodobit cu doua
volute in forma de spirala, care aminteste de cochilia unui melc. Acoperisul se
sprijina pe aceste volute. Totul pare plin de abundepta, eleganta si exuberanta.
Ordinui corintic este si mai plin de gratie caci coloanele lui sunt mai inalte
inca, de zece ori cat diametrul, iar capitelurile sunt impodobite cu frunze de
acant. La aceasta geometrie a colonelor trebuie adaugata si seria de calcule
cerute de intreaga structura a templului, calcule care au la baza raportul
taieturii de aur. Desigur ca, consideratiile legate de stabilirea proportiilor
dintre diferitele parti componente nu au restrans in nici un fel geniul sau
libertatea artistului. Arhitectul grec nu a fost robul calculelor sale ci,
odata stabilite, el a introdus modificarile care se impuneau pentru ca sa dea
edificiului armonie si eleganta. Iata un exemplu surprinzator : Partenonul,
templul inchinat zeitei Atena Partenos, a fost cladit in stilul doric,
considerandu-se ca numai acest stil poate exprima, prin caracterul lui grav si
sever, toate calitatile si atributele falnicei zeite. Dar, daca facem o
comparatie intre templul lui Poseidon si Partenon, ramanem uimiti de deosebirea
dintre aceste doua cladiri, executate in acelasi stil. Masuratorile, care au
fost intr-adevar facute, in secolul al XIX-lea, au aratat ca toate liniile
orizontale ale Panteonului sunt usor ingrosate la mijloc si astfel liniile care
par drepte orizontale sunt, in realitate, linii curbe convexe si, in acelasi
timp, peretii si muchiile verticale sunt, in realitate, nu linii drepte, ci
linii concave. Arhitectul Ictinius, care a zidit templul, a folosit acest
artificiu, pe care ochiul liber nu-l poate sesiza, ca sa evite impresia de
monotonie a liniilor drepte, dupa cum, manta de aceeasi cauza, geniul Phidias a
adaugat decoratii sculpturale la frize, metope sip e fronton. Prin asemenea
modificari la impresia de masivitate si de sobrietate s-a adaugat aceea de
eleganta si armonie care a marit efectul artistic.
|

|
Romanii, care nu au excelat prin talente matematice, au introdus totusi
un element geometric in arhitectura lor, anume bolta in forma de jumatate de
sfera si arcul in plin cintru, adica format dintr-un semicerc.
|
|

|
Prin aceste inovatii ale arhitectilor romani preluate de la etrusci,
aduse si de acestia din Orient, s-a creat, pe de o parte, un stil propriu ,si
original si, pe de alta parte, o soliditate a constructiilor care se aseamana
cu aceea realizata de egipteni prin folosirea enormelor blocuri de piatra
cioplita.
|
Celebrele arcuri de triumf prin care romanii cinsteau pe generalii ce se
intorceau la Roma incarcati de glorie si succese au o forma geometrica precisa,
plina de armonie si eleganta. Anume, arcul de triumf este format mai intai din
suprafafa laterala a unei jumatati de cilindru circular drept si apoi din
volumele paralelipipedice pe care se sprijina suprafata cilindrica, acestea
fiind impodobite cu coloane, de obicei corintice, si cu diferite sculpturi. De
atunci si pina azi, astfel de monumente, care exprima mandria fortei
triumfatoare impodobesc pietele celor mai multe dintre capitaleIe tarilor din
Europa. Un alt monument roman, tot de forma geometrica, anume un trunchi de con
inalt de 44 m la care se adauga altele ale caror dimensiuni au fost calculate
astfel incat sa asigure stabilitatea coloanei si estetica ei, este Columna lui
Traian, atit de importanta pentru istoria tarii noastre. Din punct de vedere
artistic sunt foarte interesante cele 34 de blocuri de marmura alba pe care
sunt sculptate peste 3 000 de personaje legate de episoadele victorioase ale
imparatului Traian fara sa mentionam si multimea cailor, armelor, drapelelor,
carelor de razboi s.a.m.d. In fine, arhitectura romana a realizat unul dintre cele
mai impunatoare amfiteatre din lume : Colosseum-ul din Roma, cu o capacitate de
vreo 80 000 de locuri. Arena este in forma de elipsa, cu axa mare de 200 m si
axa mica de 167 m, iar zidul are, de jur imprejur, forma unui cilindru si este
compus din patru etaje toate formate din arcade. Primul etaj este construit din
coloane dorice, masive, al doilea din coloane ionice, avand capitelurile ornate
cu volute, al treilea din coloane corintiu, iar al patrulea etaj are stalpii de
sustinere in forma de prizme. Desigur ca, pentru arhitectii greci, un asemenea
amestec de stiluri ar fi echivalat cu o curata barbarie, cu atat mai mult cu
cat si ultimul etaj, care s-ar fi cerut sa fie cel mai suplu si usor, se
prezenta a fi cel mai masiv si greoi. Pentru contemporani si cei ce au urmat,
aceasta inovatie a arhitectilor romani a trezit insa un sentiment de admiratie
si a fost considerat demn de a fi imitat, fapt care a si dainuit pina in
secolul al XII-lea.
Abia prin a doua jumatate a secolului al XII-lea, aIaturi de arta romana a
aparut arta gotica in care semicercul roman a fost inlocuit prin intersectia a
doua arce de cerc, formand ogiva. Denumirea de arta gotica a fost data la
inceput in sens peiorativ caci ea nu are nimic comun cu gotii, noua arta
nascandu-se in Franta. Elementul caracteristic al acestei arhitecturi se
bazeaza tot pe o constructie geometrica. Iata o metoda simpla de a construi
cateva feluri de ogive, toate avand aceeasi baza AB, ca si semicercul
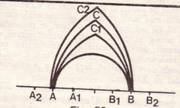
corespunzator. Sa impartim segmental AB in patru parti egale sis a consideram
AA1=BB1=AB/4. De o parte si de alta a punctelor A si B se iau punctele A2 si B2
simetrice fata de A si respectiv B.
Apoi, din A2 ca centru si cu o raza egala cu A2B se descrie arcul de cerc BC,
iar din B, ca centru si cu aceeasi raza se descrie arcul AC2. Am obtinut astfel
ogiva AC2B. Procedind la fel, dar folosind drept centre punctele A si B, iar ca
raza AB, se capata ogiva ACB sau daca se iau ca centre ale arcelor de
intersectie punctele A1 ,si B1, iar ca raza comuna distanta A1B =AB1, ogiva
obtinuta este AC1B. Din acest exemplu, care poate fi variat prin schimbarea
valorilor atribuite segmentelor AAa, BB1, arcadele gotice prin care se
inlocuieste arcada semicirculara romana pot fi oricat de inalte si ascutite,
cele doua arce de cerc indepartandu-se astfel tot mai mult de baza lor AB.
Acest nou stil care a dat catedralelor gotice multa eleganta si descatusindu-le
de semicerc si semisfera care le tineau legate de pamint, le-au permis sa se
avinte spre cer, a cucerit toate tarile din Europa occidentala in afara de
Italia. In Franta, Germania, Olanda, Spania, Portugalia, Anglia s-au gasit
multi artisti arhitecti care au proiectat si au zidit admirabile catedrale
gotice. In ale caror dimensiuni se gaseste, ca un ghid, taietura de aur, si triunghiul
echilateral. 'In Italia insa artistii, ca si oamenii de stiinta, s-au
indreptat, plini de nostalgie, catre vechile orase romane, cu palatele si
monumentele lor in ruina si au cautat sa reconstituie tehnica de odinioara. La
inceputul secolului al XV-lea arhitectul si artistul Brunelleschi a ridicat
prima constructie in noul stil al Renasterii, catedrala din Florenta, numita si
Campanila (Clopotnita), cel mai inalt si mai larg dom de atunci. Cupola sa este
semisferica, iar boltile in plin cintru. Acesteia i-au urmat alte edificii de
acelasi fel in care arta greco-romana a renascut sub o noua forma, plina de
ornamente bogate. In acelasi stil a inceput la Roma, in secolul urmator,
construirea bazilicei Sf. Petru de catre recunoscutii mari artisti : Bramante
,si Michelangelo. Ea a fost terminata in prima jumatate a secolului al XVII-lea
de arhitectul-sculptor Gian Lorenzo Bernini, ultimul mare artist al Renasterii,
care a renovat si piata din fata bisericii, intr-o forma ce este considerata
pana azi ca "una dintre cele mai geniale solutii urbanistice pe care le
cunoaste istoria arhitecturii', Arhitectul Bernini a fost un mare geometru
si a stiut sa puna geometria in slujba frumusetii. El afirma ca "frumusetea
tuturor lucrurilor din lume consta in proportii'. De exemplu, ovalul
pietii Sf. Petru a fost construit din doua cercuri secante de aceeasi raza in
asa fel incat axa longitudinala sa aiba lungimea de trei raze. Mai mult,
Bernini avea o fantezie foarte bogata, si decoratiile de origine romana pe care
le-a folosit au placut atat de mult incat s-au raspindit in toata Europa sub
numele de stil baroc. De aceasta bogata fantezie s-a servit si cind a construit
Scala Regia de la Vatican. El a dispus de o coloana de sectiune descrescinda si
s-a folosit de convergenta peretilor in asa fel incst scara sa para mai lunga
decit este in realitate. Cind cineva o urca, are surpriza de a constata ca este
mult mai scurta decit parea.
Odata cu inceputul secolului XX, arhitectura a trebuit sa capete o noua
infatisare din cauza noilor conditii de viata. Trebuia sa se gaseasca solutii
problemei de a acoperi spatii vaste cu cladiri in care sa locuiasca, in
conditii bune, multimi numeroase, folosindu-se materiale de constructii noi ca
fierul ,si betonul armat. Intr-o frumoasa carte aparuta la noi in tara,
arhitectul Marcel Melicson observa ca azi arhitectura se indreapta catre un
frumos rational: "Orice organrism este cu atit mai frumos cu cit este mai bine
adaptat scopurilor sale. Intr-o opera cu adevarat frumoasa, nimic nu este lasat
la voia intimplarii, totul este justificat, util, totul se indreapta spre
rezultatul urmarit. Frumusetea suprema, capodopera artistica, stralucita
manifestare a geniului este in acelasi timp triumful ratiunii'. Acelasi
autor citeaza urmatoarele randuri din cartea altui arhitect celebru, Le Corbus
intitulata Sfire o arhitectura : "Cuburile, conurile, sferele, cilindrii,
piramidele sunt marile forme primare pe care lumina le scoate in evidenta,
imaginea lor este precisa, fara neclaritate. De aceea sint forme frumoase, cele
mai frumoase forme Axele, cercurile, unghiurile drepte sunt adevarurile
geometriei ; altfel ar fi hazard, anomalie, arbitrar. Geometria este limbajul
omului. Marile probleme ale constructiei moderne vor fi realizate prin geometrie.
Linia dreapta aduce sanatate sufletului oraselor Gasim linia dreapta in
toata istoria omenirii, in orice act uman.. Dreapta este o reactie, o actiune,
miscare, efectul unei autodeterminari. Dupa mai bine de 30 de ani, preocupat
tot de aceasta problema a banismului, Le Corbussier adauga : "Compozilia
arhitectonica este geometrica, eveniment de ordin vizual in primul rind,
eveniment antrenind judecatile de cantitate, de raporturi, aprecieri de
proportii. Proportia provoaca senzatii, iar perindarea acestor setiza
corespunde melodiei din muzica.' Dar, in epoca actuala, a cladirilor
gigantice, la planurile pentru fabricile construite pe sute de hectare, baraje
sau hidrocent colosale, scara de proportii, mai potrivita, pe care anumit-o
modulor. Cuvantul este format din doi termini; primul: modul inseamna tocmai
raport sau scara de proportie, iar al doilea or este numirea franceza
corespunzatoare in romaneste substantivului aur, asadar: modulor are, de fapt,
aceeasi semnificatie ca si taiatura de aur, numai ca dimensiunile raportului
sunt altele decat acelea folosite in Antichitate sau Renastere. Modulorul se
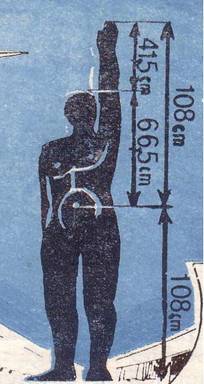
obtine considerind un om de statura mijlocie stand in picioare cu un brat
ridicat in sus, asadar de o lungime de 216 cm. In acest caz, ombilicul lui
imparte acest segment in doua parti egale de cite 708 cm. Aceasta este lungimea
segmentului AB, considerat odinioara de Euclid, si acest segment de 108 cm este
impartit in taietura de aur prin distante de la virful degetelor pina la cap
(41,5 cm) si segmentul ramas, de la varful capului la ombilic (66,5 cm). Cu
accste dimensiuni, Le Corbussier a format un sir de numere care poarta numele
de scara modulor, in care termenii se obtin astfel ca oricare dintre ei este
egal cu suma a doi tevmeni dinaintea lui : 41,5 ; 66,5 ; 108 ; 174,5 ;
Oricare doi termeni alaturati, din scara modulor, au inca si proprietatea
ca sunt in aceeasi proportie, aceea data de taietura de aur si de ea se
folosesc arhiteclii de azi ca sa stabileasca diferitele dimensiuni ale unei
cladiri cind urmaresc sa-i dea un aspect arrponios.
Trebuie, insa, sa-ti atrag atentia, draga cititdrule, ca aceasta scara de
proportii nu-i suficienta ca o cladire sa se prezinte sub o infatisare plina de
armonie si echilibru si sa stirneasca admiratia celui ce o contempla. Aceasta
ramine o problema pe care nu o poate rezolva decit talentul arhitectului
respectiv. O afirma chiar autorul: "Modulorul nu da talent si inca mai putin
geniu. El nu subtiaza ceea ce nu este subtire, el ofera doar placerea si
increderea care poate rezulta din folosirea masurilor sigure'. Arta
inseamna cu totul altceva decat formula matematica, insa, daca esti artist,
atunci modulorul te ajuta, asa cum ajuta si dalta pe un sculptor sau un pian,
bine acordat, pe un pianist.