Determinarea validitatii in cazul
inferentelor cu propozitii compuse
Dupa cum am aratat mai inainte,
tabelele de adevar, folosite initial pentru a defini cei cinci
conectori logici verifunctionali, pot fi folosite si pentru a
determina daca o formula este lege logica sau nu. Cum
inferentelor valide le corespund o subclasa a legilor logice, si
anume clasa tautologiilor in cadrul carora operatorul principal este o
implicatie logica, vom putea folosi tabele de adevar pentru a
testa validitatea inferentelor cu propozitii compuse. Aceasta
metoda se va numi metoda tabelelor de adevar.
Fie urmatorul rationament:
"Daca Andreea se casatoreste cu Victor, atunci Iuliana
si Ana vor fi domnisoare de onoare. Daca Iuliana si Ana vor
fi domnisoare de onoare, atunci Mihai si George vor fi cavaleri de
onoare. Dar Andreea se casatorsete cu Victor sau Mihai si
George vor fi cavaleri de onoare. In consecinta, Iuliana si Ana
vor fi domnisoare de onoare sau Mihai si George vor fi cavaleri de
onoare."
Schema logica a acestui argument este
reprezentata de urmatoarea inferenta:

Acestei scheme inferentiale ii corespunde
urmatoarea formula propozitionala:
[(p→q) & (q→r) & (p r)] → (q r),
pe care o vom nota cu A(p,q,r).
Acesteia ii construim tabelul de adevar
corespunzator:
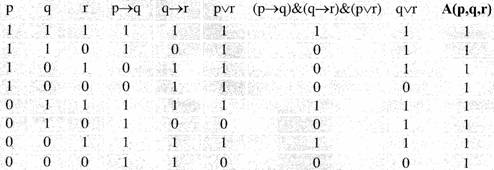
Dupa cum se poate vedea, intrucat coloana
din tabel corespunzatoare formulei noastre nu contine decat 1,
rezulta ca formula este o tautologie, deci inferenta
corespunzatoare formulei in cauza este valida.
Sa luam acum ca exemplu argumentul
folosit de filozoful David Hume impotriva credintei crestine in "viata
de apoi":
"Daca exista dreptate in
aceasta viata, atunci nu este nevoie de o viata
viitoare. Daca, pe de alta parte, nu exista dreptate in viata
noastra pamanteasca, atunci nu avem niciun motiv sa credem ca
Dumnezeu este drept. Dar daca nu avem niciun motiv sa credem ca
Dumnezeu este drept, atunci nu avem niciun motiv sa credem ca El ne
va asigura o viata viitoare. Astfel, sau nu este nevoie de o viata
viitoare, sau nu avem niciun motiv sa credem ca Dumnezeu ne va
asigura o astfel de viata."
Schema logica a acestui argument este
reprezentata de urmatoarea inferenta:

Acestei scheme logice ii corespunde
urmatoarea formula propozitionala:
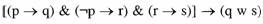
Pentru o astfel de formula, fiind vorba
de patru variabile propozitionale, tabelul de adevar corespunzator
este unul mult prea complex. In astfel de cazuri se poate folosi metoda deciziei prescurtate,
denumita si metoda tabelelor
(de adevar) partiale. Aceasta metoda se bazeaza pe
proprietatea implicatiei logice de a nu admite cazul in care antecedentul
acesteia este adevarat si consecventul fals. Presupunem deci, prin
reducere la absurd, ca antecedentul inferentei noastre, respectiv conjunctia
premiselor, este adevarat, iar consecventul fals. Daca in urma
acestei presupuneri ajungem la o contradictie (imposibilitate logica),
rezulta ca presupunerea (potrivit careia formula este
inconsistenta) a fost falsa, deci ca formula in cauza este
valida.
In cazul nostru, acest lucru se va
desfasura astfel: presupunem ca formula nu reprezinta o
lege logica, deci ca este inconsistenta. Rezulta de aici
ca vom avea cel putin un caz cand antecedentul inferentei este
adevarat si consecventul fals. Consecventul implicatiei este
constituit din disjunctia exclusiva"q w s". Din tabelul de valori
corespun-zator disjunctiei exclusive, stim ca aceasta este
falsa cand ambii membri au aceeasi valoare de adevar. Vom avea
astfel doua cazuri, fie cand ambele propozitii sunt adevarate,
fie cand ambele sunt false:
1) Sa analizam acum cazul cand cele
doua propozitii disjuncte ce formeaza concluzia sunt ambele
false, respectiv cand V(q) = 0 si V(s) = 0 (prin V(p) intelegem
"valoarea de adevar a lui p", unde p reprezinta o propozitie).
Stim totodata ca antecedentul
este adevarat. Cum antecededentul este constituit din conjunctia a
trei formule conditionale, si cum din definitia conjunctiei
stim ca aceasta este adevarata doar daca toti
membrii acesteia sunt adevarati, rezulta ca fiecare dintre
aceste formule conditionale trebuie sa fie la randul ei
adevarata. In cazul primei implicatii, vom avea V(p → q) =
1, dar cum V(q) = 0 rezulta ca V(p) ≠ 1, deci V(p) = 0. In
cazul celei de-a treia implicatii, stim ca V(r → s) = 1 si ca V(s) = 0, de unde
rezulta de asemenea
ca
V(r) ≠ 1, deci ca V(r) = 0. Dar
pentru ca antecedentul sa fie adevarat, trebuie si ca cea de-a
doua implicatie sa fie adevarata, respectiv ca sa avem
V(¬p → r) = 1. Acest lucru este insa imposibil, intrucat cum V(p) =
0, atunci V(¬p) = 1, iar din faptul ca V(r) = 0 vom avea ca V(¬p
→ r) = 0. Evident, cum o formula propoziionala nu poate fi
simultan si falsa si adevarata, rezulta ca
am ajuns la o contradictie logica, deci, presupunerea initiala
este falsa, iar formula analizata este valida.
2) Sa luam acum cazul cand cei doi disjuncti
sunt ambii adevarati, respectiv V(q) = 1 si V(s) = 1. Conform
presupunerii initiale, antecedentul este adevarat. Cum antecedentul
este constituit din conjunctia a trei formule conditionale, si cum
din definitia conjunctiei stim ca aceasta este adevarata
doar daca toti membrii acesteia sunt adevarati,
rezulta ca fiecare dintre aceste formule conditionale trebuie
sa fie la randul ei adevarata. In cazul primei implicatii
vom avea V(p→q) = 1, si cum V(q) = 1, rezulta ca V(p) = 0
sau V(p) = 1. Observam ca in acest caz nu putem sa
determinam pe baza proprietatilor implicatiei valoarea propozitiei "p". In cazul celei de-a treia implicatii,
stim ca V(r → s) = 1 si ca V(s) = 1, de unde
rezulta de asemenea ca V(r) = 1 sau ca V(r) = 0. Dar pentru ca
antecedentul sa fie adevarat, trebuie ca si cea de-a doua implicatie
sa fie adevarata, respectiv V(¬p → r) = 1. Cum am
vazut insa, este posibil sa avem V(r) = 1 si V(p) = 1, deci
V(¬p) = 0, de unde rezulta, din definitia implicatiei, ca
V(¬p → r) 1. In acest caz, nu am ajuns la nicio contradictie
logica, drept pentru care vom spune ca formula in cauza este nevalida,
intrucat exista cel putin un caz cand aceasta este falsa. Acest
caz este cand V(p) = 0, V(q) = 1, V(r) = 1 si V(s) = 1.
Operatia prin care dam valori literelor
propozitionale se numeste interpretare a formulei in cauza. Cum
am gasit o astfel de interpretare, rezulta ca formula nu este o
lege logica, deci, inferenta corespunzatoare acesteia este
nevalida. Este de remarcat ca in cazul in care concluzia
implicatiei ar fi fost "¬q & ¬s", argumentul ar fi fost valid.
Insa tocmai aceasta concluzie voia Hume sa o infirme




