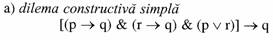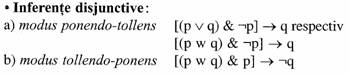Tautologii remarcabile
Din punct de vedere logic, toate tautologiile
sunt formule logic echivalente intre ele. Unele dintre acestea sunt insa
mai utile si mai importante in procesul de recunoastere a relatiilor
logice dintre propozitii. Iata cateva legi logice fundamentale
(ramane drept exercitiu sa aratati, prin procedeul
tabelelor de adevar, ca sunt tautologii):
1.
Lista tautologiilor remarcabile

Tautologii remarcabile sunt si "legile
lui De Morgan", care redau raportul de dualitate
dintre conjunctie si disjunctie. Raportul de dualitate
reprezinta o relatie de simetrie, in sensul in care unul dintre
termeni poate fi definit in raport cu celalalt, si reciproc. De
exemplu, in geometrie "punct" si "dreapta" reprezinta termeni
duali: "Doua puncte determina o dreapta" si "Intersectia
a doua drepte determina un punct". In logica, un exemplu de
termeni duali este: "gen" si "specie": Acest raport de dualitate revine la
a observa ca daca in tabelul de adevar al conjunctiei inlocuim
peste tot pe 1 cu 0 si pe 0 cu 1, vom obtine tabelul de adevar
al disjunctiei, si reciproc:
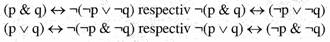
Trebuie adaugat ca operatorii
conjunctie si disjunctie sunt distributivi unul fata
de altul:
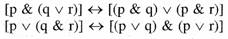
Iata alte cateva tautologii:

2.
Inferente cu propozitii compuse
Aceste formule, ce constituie legi logice,
reprezinta scheme valide de rationamente in limbajul natural. Sa
luam, de exemplu, urmatorul rationament: "Daca alerg repede
pana in statia de autobuz, voi prinde autobuzul de ora doua.
Daca voi prinde autobuzul de ora doua, atunci voi ajunge la timp la
film. Deci, daca alerg repede, atunci voi ajunge la timp la film". Avem
aici urmštoarea schema de rationament:

Schema rationamentului corespunde unei
formule prezentate mai inainte, respectiv tranzitivitatii implicatiei:
[(p → q) & (q → r) →
(p → r). Cum aceasta reprezinta o lege logica,
rationamentul este valid. In cazul in care nu putem identifica schema
logica a unui rationament cu o tautologie, vom construi tabelul de
adevar corespunzštor formulei in cauza si ii vom testa astfel
validitatea.
Vom prezenta in continuare cateva formule
propozitionale care constituie scheme logice ale unor rationamente
deductive cunoscute in practica argumentarii. Vom adopta denumirea
moderna de "inferenta" pentru "rationament", deoarece se
considera ca termenul "rationament" din logica traditionala
are un inteles psihologic, care trebuie evitat in cazul unei abordari
logice.
Trebuie adaugat ca orice inferenta
valida are la baza o lege logica, dar nu orice lege logica
este si o inferenta. Sunt inferente doar expresiile ce se
prezinta sub forma unei implicatii sau a unei echivalente.
Vom prezenta mai intai inferente cu doua
premise, pentru care s-a incetatenit si denumirea de "moduri".
Acestea sunt de doua feluri: ipotetice si disjunctive.

Modus
ponens mai este cunoscut si
sub denumirea de "formula de eliminare a conditionalului". Acesta spune
ca daca implicatia intre doua propozitii este
adevarata si daca antecedentul acesteia este adevarat,
atunci si consecventul implicatiei initiale este adevarat.

Modus
tollens spune ca
daca implicatia intre doua propozitii este
adevarata si daca consecventul acesteia este fals, atunci si
antecedentul implicatiei este fals.

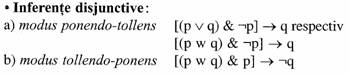
Modus
tollendo-ponens spune ca
daca este adevarata disjunctia a doua propozitii,
iar una dintre acestea este falsa, rezulta ca cealalta
propozitie este adevarata. De observat ca acest mod este
valid atat in cazul disjunctiei exclusive, cat si in cazul celei
inclusive.

Modus
ponendo-tollens spune ca
daca este adevarata disjunctia a doua propozitii,
iar una dintre acestea este adevarata, atunci cealalta propozitie
este falsa. Acest mod este valid doar in cazul disjunctiei exclusive.
(Ramane ca exercitiu sa aratati de ce nu este valid in
cazul disjunctiei inclusive.)

Denumirile latine ale acestor moduri marcheazš
calitatea celei de-a doua premise si a concluziei. Astfel, prin "ponendo"
se intelege ca premisa este asertata, respectiv, prin
"tollendo", ca aceasta este respinsa. Prin "ponens" si "tollens"
ni se indica daca avem concluzie afirmativa, respectiv
negativa.
Inferente
ipotetico-disjunctive (dileme):
Inferentele cu mai mult de doua
premise se regasesc in genere in logica sub numele de dileme. In continuare,
vom prezenta patru tipuri dintre acestea, care combina in anumite feluri
modurile studiate mai inainte. Acestea sunt "simple" sau "complexe", in functie
de faptul daca concluzia este o propozipe simpla sau complexa.
Ele mai sunt impartite in "constructive" sau "distructive", in functie
de faptul daca concluzia contine propozitii afirmative sau
negative.