Determinarea
solutiilor optime cu functii criteriu in limbaj intrare-stare-iesire, fara timp
final impus
1. Folosirea limbajului intrare-stare-iesire
Limbajul intrare-stare-iesire poate fi
folosit atat pentru descrierea functionarii sistemelor de reglare in functie de
marimile de iesire - cu schema din figura 1.13 - cat si pentru descrierea
functionarii sistemelor de reglare in functie de stare. In paragraful 5.1.4 a
fost ilustrata trecerea de la ecuatiile diferentiale in functie de eroare si
derivatele ei, respectiv in functie de componenta tranzitorie 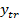 si
derivatele ei (deci de la descrierea intrare-iesire) la ecuatiile de stare
(deci la descrierea intrare-stare-iesire) pentru un sistem de reglare in
functie de marimile de iesire, cu blocul de reglare instalat pe calea directa,
ca in figura 1.13
si
derivatele ei (deci de la descrierea intrare-iesire) la ecuatiile de stare
(deci la descrierea intrare-stare-iesire) pentru un sistem de reglare in
functie de marimile de iesire, cu blocul de reglare instalat pe calea directa,
ca in figura 1.13
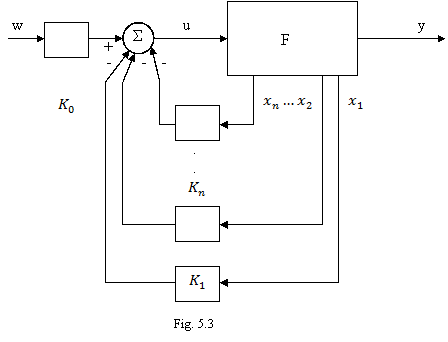
In cazul reglarii functie de stare,
schema de elemente are aspectul din figura 5.3, in ipoteza unui sistem cu o
marime de referinta 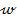 si cu o marime de
iesire y; blocurile de reglare - cu
factorii de proportionalitate
si cu o marime de
iesire y; blocurile de reglare - cu
factorii de proportionalitate 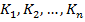 - sunt
instalate pe reavtiile in functie de marimile de stare
- sunt
instalate pe reavtiile in functie de marimile de stare 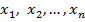 care
formeaza vectorul n-dimensional x.
care
formeaza vectorul n-dimensional x.
Daca se alege marimea de iesire y
ca una din marimile de stare de exemplu
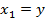 (1)
(1)
atunci se adopta
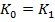 (2)
(2)
si se obtine o
anumita combinare a reglarii functie de stare cu reglarea functie de iesire.
Astfel, din figura 5.3 se obtine pentru
marimea de comanda u expresia
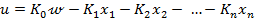 (3)
(3)
si introducand (1)
si (2) in (3) rezulta
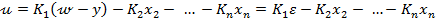 (4)
(4)
avand in vedere (1.61).
Reglarea functie de stare presupune
asigurarea accesibilitatii pentru masurarea tuturor starilor; cand starile nu
sunt accesibile, se folosesc estimatoare de stare [1].
In cazul general, cand nu are loc relatia
(1), se poate adopta
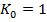 (5)
(5)
si relatia (3)
capata aspectul
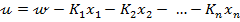 (6)
(6)
respectiv
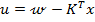 (7)
(7)
considerand ca
parametrii 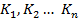 ai
regulatorului reprezinta componentele unui vector K:
ai
regulatorului reprezinta componentele unui vector K:
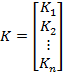 (8)
(8)
Optimizarea dinamica are ca scop
determinarea valorilor optime ale parametrilor 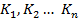 ai
regulatorului, prin minimizarea unei functii criteriu. In prezentul subcapitol
sunt considerate criterii de forma
ai
regulatorului, prin minimizarea unei functii criteriu. In prezentul subcapitol
sunt considerate criterii de forma 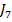 din (2.7),
fara timp final
din (2.7),
fara timp final 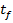 impus,
criteriile cu un timp final impus fiind considerate in subcapitolul 5.
impus,
criteriile cu un timp final impus fiind considerate in subcapitolul 5.
Determinarea valorilor optime 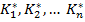 ale
parametrilor regulatorului implica si determinarea comenzii optime
ale
parametrilor regulatorului implica si determinarea comenzii optime 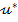 , in conformitate cu (7).
, in conformitate cu (7).
Pentru sistemele multivariabile, cu mai
multe marimi de referinta care formeaza un vector m-dimensional w , cu mai
multe marimi de iesire formand vectorul m-dimensional
y si cu mai multe marimi de comanda
formand vectorul m-dimensional u,
relatia (7) capata aspectul
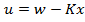 (9)
(9)
matricea K avand
dimensiuni m x n.
2 Determinarea solutiei optime in conformitate cu
functia criteriu 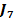
Considerand ca blocul partii fixate F
(fig. 5.3) este liniar, multivariabil si functionarea sa este descrisa de
ecuatiile de stare
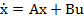 (10)
(10)
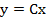 (11)
(11)
se adopta pentru
optimizare criteriul
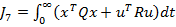 (12)
(12)
unde matricele de
ponderare Q si R sunt simetrice si pozitiv definite (matricea Q poate fi si pozitiv semidefinita) si au dimensiunile n x n,
respective m x m. Matricele Q si R pot si astfel alese incat sa asigure
efecte suplimentare de optimizare, in sensul localizarii radacinilor ecuatiei
caracteristice in anumite domenii ale planului complex, rezultand astfel indici
suplimentari de calitate a procesului tranzitoriu.
Intrucat criteriul 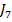 se refera
numai la regimul tranzitoriu spre deosebire de criteriile
se refera
numai la regimul tranzitoriu spre deosebire de criteriile 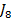 si
si 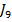 din (2.8)
si (2.9), la care apare un timp final impus
din (2.8)
si (2.9), la care apare un timp final impus 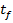 si intervin
si termini aferenti noului regim stationar se poate considera conventional.
si intervin
si termini aferenti noului regim stationar se poate considera conventional.
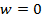 (13)
(13)
ceea ce inseamna ca in noul regim stationar se va
obtine 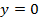 , deci
, deci 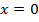 , conform cu (11). Asemenea situatii intervin, de
exemplu cand vectorul x reprezinta abaterea de la o evolutie dorita.
, conform cu (11). Asemenea situatii intervin, de
exemplu cand vectorul x reprezinta abaterea de la o evolutie dorita.
Din (9) si (13) rezulta ca in acest caz
intre vectorii de comanda u si de
stare x are loc relatia
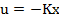 (14)
(14)
si deci in noul
regim stationar se va obtine si 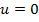
Tocmai faptul ca dupa incheierea
regimului tranzitoriu, la 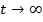 , va rezulta
, va rezulta
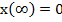 (15)
(15)
si
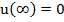 (16)
(16)
asigura o valoare
finite a integralei 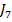 din (12) si
deci posibilitatea determinarii unei comenzi optimale
din (12) si
deci posibilitatea determinarii unei comenzi optimale 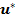 care
minimizeaza valoarea integralei; daca in noul regim stationar nu ar fi
indeplinite conditiile (15) si (16), atunci integrala
care
minimizeaza valoarea integralei; daca in noul regim stationar nu ar fi
indeplinite conditiile (15) si (16), atunci integrala 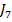 ar avea o
valoare infinita si problema minimizarii nu s-ar putea pune.
ar avea o
valoare infinita si problema minimizarii nu s-ar putea pune.
Notand cu 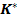 matricea
parametrilor optimi ai regulatorului, comanda optimala
matricea
parametrilor optimi ai regulatorului, comanda optimala 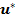 - care asigura minimizarea
criteriului
- care asigura minimizarea
criteriului 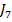 - are
expresia
- are
expresia
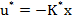 (17)
(17)
conform cu (14).
Pentru asigurarea existentei unei
solutii optimale, partea fixata F - descrisa de (10) si (11) - trebuie sa fie
complet controlabila [1,3,12,13].
Conditia de controlabilitate fiind
asigurata, se presupune ca exista o lege de reglare in functie de stare, de
forma
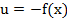 (18)
(18)
care asigura
obtinerea unui sistem asimptotic stabil [6] si minimizeaza criteriul 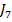
Expresia matricei 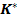 poate fi
obtinuta prin intermediul functiilor Liapunov. Notand - ca si in paragraful
5.1.4 - integrandul (aferent criteriului
poate fi
obtinuta prin intermediul functiilor Liapunov. Notand - ca si in paragraful
5.1.4 - integrandul (aferent criteriului 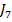 ) prin
) prin
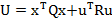 (19)
(19)
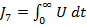 (20)
(20)
Matricele Q si R fiind pozitiv
definite, functia U este pozitiv
definita.
Ca si in (3.53), functia Liapunov pozitiv
definita V trebuie astfel aleasa
incat sa se obtina - in virtutea ecuatiei de stare a sistemului
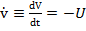 (21)
(21)
Introducand (18) in (10), ecuatia de
stare capata aspectul
 (22)
(22)
iar din (18) si (19)
rezulta
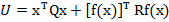 (23)
(23)
Inlocuind (23) in
(21) se obtine
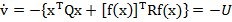 (24)
(24)
si deci derivata 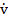 este
negativ definita, functia U fiind
pozitiv definita.
este
negativ definita, functia U fiind
pozitiv definita.
Derivata 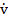 poate fi
pusa sub forma
poate fi
pusa sub forma
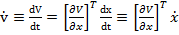 (25)
(25)
si introducand (22)
in (25) se obtine expresia derivatei 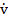 in virtutea ecuatiei
de stare:
in virtutea ecuatiei
de stare:
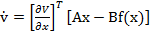 (26)
(26)
Din (24) si (26)
rezulta
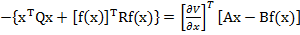 (27)
(27)
Prin derivaera
partiala a expresiei (27) in raport cu f(x) se obtine
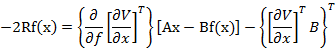
respectiv
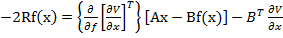 (28)
(28)
Din (20) si (21)
se obtine
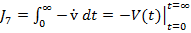 (29)
(29)
relatie analoaga
cu (2.72)
Ca si in (2.73) se poate scrie
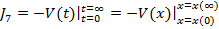 (30)
(30)
Avand in vedere (15) si notand
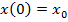 (31)
(31)
expresia (30)
capata forma
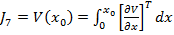 (32)
(32)
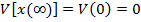 (33)
(33)
functia V fiind pozitiv definita.
Legea de reglare (18) devine optimala
daca minimizeaza expresia 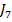 din (32),
fiind deci necesara conditia
din (32),
fiind deci necesara conditia
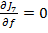 (34)
(34)
Avand in vedere (32), conditia (34)
capata aspectul
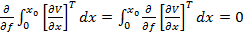 (35)
(35)
Pentru ca relatia (35) sa fie satisfacuta
(pentru orice valori initiale 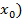 este
necesara conditia
este
necesara conditia
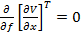 (36)
(36)
Datorita
relatiei (36), expresia (28) capata forma
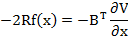
si rezulta astfel
legea de reglare
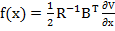 (37)
(37)
ramanand sa fie
determinata derivata partiala 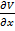 .
.
In acest scop se introduce (37) in (27)
si se obtine

respectiv
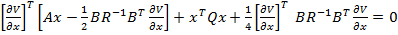 (38)
(38)
(matricea R fiind simetrica) sau
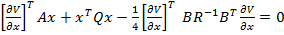 (39)
(39)
Intrucat are loc
egalitatea
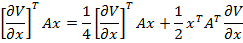
relatia (39)
poate fi pusa sub forma
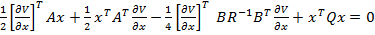 (40)
(40)
Expresia (40) arata ca egalitatea va fi
satisfacuta daca exista o dependenta liniara a gradientului 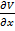 in functie
de vectorul de stare x, de forma
in functie
de vectorul de stare x, de forma
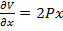
matricea
simetrica pozitiv definita P satisfacand ecuatia matriceala algebrica Riccati
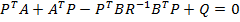 , (41)
, (41)
deoarece prin
introducerea expresiei gradientului in (40) se obtine
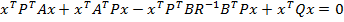 (42)
(42)
Intrucat (42) se obtine din (41)
inmultind la stanga cu 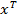 si la
dreapta cu x, asigurarea egalitatii (41) implica si satisfacerea relatiilor (42) si (40), deci legea de reglare (37) cu
adoptarea expresiei mentionate a gradientului - asigura minimizarea criteriului
si la
dreapta cu x, asigurarea egalitatii (41) implica si satisfacerea relatiilor (42) si (40), deci legea de reglare (37) cu
adoptarea expresiei mentionate a gradientului - asigura minimizarea criteriului
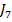 , satisfacand conditiile (34) si (36).
, satisfacand conditiile (34) si (36).
Intrucat matricea P este simetrica,
ecuatia Riccati (41) capata forma
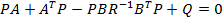 (43)
(43)
Matricele A, B, Q si R fiind cunoscute
din datele initiale (10) si (12), matricea P se obtine prin rezolvarea ecuatiei
(43).
Inlocuind (37) in (18) si avand in vedere
expresia gradientului, se obtine comanda optimala
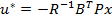 (44)
(44)
respectiv -
comparand (17) cu (44) - rezulta matricea parametrilor optimi ai regulatorului
in functie de stare
 (45)
(45)
3. Valoarea minima a criteriului 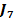 , obtinuta prin comanda optimala
, obtinuta prin comanda optimala
Considerand ca partea fixata F
este descrisa de ecuatiile de stare (10), (11) si adoptand un criteriu de forma
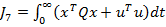 (46)
(46)
- care rezulta
din (12) adoptand 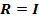 , I fiind matricea unitate - valoarea minima
, I fiind matricea unitate - valoarea minima 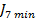 asigurata
de comanda optimala (44) poate fi obtinuta pornind de la egalitatea
asigurata
de comanda optimala (44) poate fi obtinuta pornind de la egalitatea
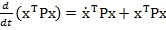 (47)
(47)
matricea
simetrica P fiind solutia ecuatiei
algebrice Riccati (43).
Inlocuind in (47) expresiile 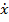 si
si 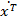 care
rezulta din (10), se obtine
care
rezulta din (10), se obtine
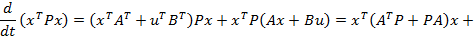
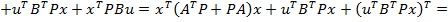
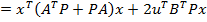 , (48)
, (48)
deoarece are loc
egalitatea marimilor scalare
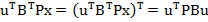 (49)
(49)
Prin integrarea expresiei (48) se obtine
 (50)
(50)
si avand in
vedere (15) rezulta
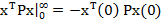 (51)
(51)
Din (50) si (51) se obtine
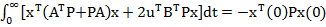 (52)
(52)
Intrucat s-a adoptat R = I, ecuatia Riccati (43)
are forma
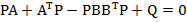
rezultand
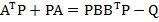 (53)
(53)
Inlocuind (53)
in (52) se obtine
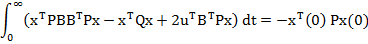
respectiv, adaugand si scazand 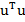 la integrand rezulta
la integrand rezulta
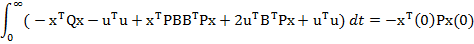
sau
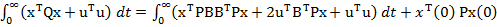 (54)
(54)
Conform cu (49) are loc egalitatea
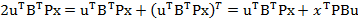 (55)
(55)
si inlocuind (55)
in (54) se obtine
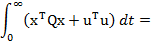
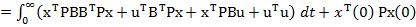 (56)
(56)
sau
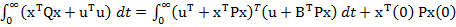 (57)
(57)
respectiv
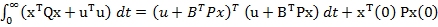 (58)
(58)
identitatea dintre expresiile (56)
si (57) verificandu-se prin efectuarea inmultirii din membrul drept.
Intrucat s-a
adoptat R = I, legea de reglare optimala (5.207 devine
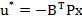 (59)
(59)
si idn (58) se
constata ca pentru 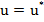 rezulta
valoarea minima a criteriului
rezulta
valoarea minima a criteriului
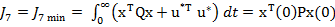 (60)
(60)
avand in vedere
si (46).
Ca si in (3.7) ,
valoarea minima a criteriului depinde de o valoare initiala, respectiv de x(0).


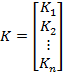 (8)
(8)