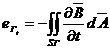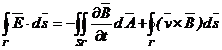Legea
inductiei electromagnetice (Faraday)
Este o lege
generala si se bazeaza pe fenomenul
de inductie electromagnetica
(M.Faraday, 1831): variatia in timp a fluxului magnetic ce
strabate orice suprafata deschisa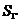 care se sprijina pe conturul inchis
care se sprijina pe conturul inchis 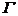 produce o t.e.m. de
contur
produce o t.e.m. de
contur 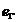 , numita si t.e.m.
indusa/solenoidala, al carei sens se opune cauzei care a
produs-o (regula lui Lenz, 1834). Se
poate scrie, ca urmare:
, numita si t.e.m.
indusa/solenoidala, al carei sens se opune cauzei care a
produs-o (regula lui Lenz, 1834). Se
poate scrie, ca urmare:
relatie
care exprima forma integrala a legii inductiei electromagnetice
si care se enunta astfel: tensiunea electromotoare de contur (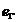 ), produsa prin inductie electromagnetica in
lungul unei curbe inchise (
), produsa prin inductie electromagnetica in
lungul unei curbe inchise (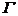 ), este egala cu viteza de scadere a fluxului
magnetic (
), este egala cu viteza de scadere a fluxului
magnetic (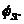 ) prin orice suprafata deschisa (
) prin orice suprafata deschisa (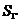 ) ce se sprijina pe curba (
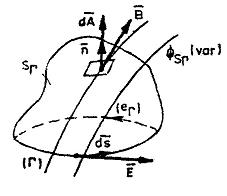
) ce se sprijina pe curba (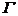 ) (fig.2.1.8). In fig.2.1.8 variatia fluxului magnetic
este scazatoare, conform semnului minus din formula (2.1.36).
) (fig.2.1.8). In fig.2.1.8 variatia fluxului magnetic
este scazatoare, conform semnului minus din formula (2.1.36).
Punand cei
doi membri ai relatiei (2.1.36) se pun sub forma:
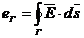
respectiv:
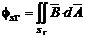
relatia
de mai inainte se mai poate scrie:
In expresia legii inductiei
electromagnetice fluxul 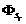 este un flux total. Daca acest flux este produs de o
bobina cu N spire, relatia
(2.1.36) devine:
este un flux total. Daca acest flux este produs de o
bobina cu N spire, relatia
(2.1.36) devine:
unde
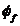 reprezinta fluxul
fascicular, adica fluxul produs de o singura spira a
bobinei.
reprezinta fluxul
fascicular, adica fluxul produs de o singura spira a
bobinei.
|
|
|
Fig. 2.1.8 Tensiunea electromotoare
indusa
|
Cum,
in general, un camp electric 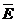 este de forma:
este de forma: 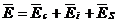 , unde Ec - campul coulombian, Ei -
campul imprimat, Es - campul solenoidal/indus,
, unde Ec - campul coulombian, Ei -
campul imprimat, Es - campul solenoidal/indus,
iar 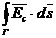 si
si 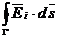 sunt nule in acest
caz, rezulta ca in expresia (2.1.37) campul
sunt nule in acest
caz, rezulta ca in expresia (2.1.37) campul 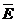 reprezinta numai
camp indus sau solenoidal (
reprezinta numai
camp indus sau solenoidal (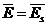 ).
).
In cazul mai general, in care domeniul cuprins de 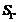 este in miscare cu viteza
este in miscare cu viteza 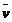 , membrul drept al relatiei (2.1.37.) se descompune, pe
baza notiunii de derivata de
flux, in doi termeni,
, membrul drept al relatiei (2.1.37.) se descompune, pe
baza notiunii de derivata de
flux, in doi termeni, 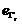 si
si 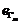 , unde:
, unde:
si
poarta numele de t.e.m. de
transformare (indusa prin variatia in timp a
intensitatii campului magnetic prin spira), iar:
si
poarta numele de t.e.m. de
miscare (de rotatie sau translatie).
T.e.m.  apare in cazul
inductiei
apare in cazul
inductiei 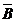 variabila in timp
si a circuitului (
variabila in timp
si a circuitului (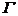 ) imobil, iar t.e.m.
) imobil, iar t.e.m. 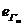 apare in cazul
inductiei
apare in cazul
inductiei 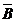 variabila sau
constanta in timp si a circuitului (
variabila sau
constanta in timp si a circuitului (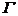 ) mobil; prima fiind specifica functionarii
transformatoarelor electrice, iar cea de-a doua - masinilor electrice
rotative, unde conturul (spirele bobinelor) taie
in miscare liniile de camp magnetic inductor.
) mobil; prima fiind specifica functionarii
transformatoarelor electrice, iar cea de-a doua - masinilor electrice
rotative, unde conturul (spirele bobinelor) taie
in miscare liniile de camp magnetic inductor.
Deducerea analitica a t.e.m. de
miscare (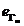 )
)
Se
considera un element 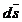 al circuitului (
al circuitului (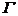 ) in miscare de translatie cu viteza
) in miscare de translatie cu viteza 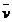 (fig. 2.1.9).
(fig. 2.1.9).
|
|
|
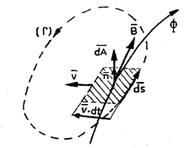
Fig. 2.1.9 Elementul 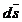 al circuitului ( al circuitului (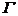 ) in miscare de translatie ) in miscare de translatie
|
Intr-un interval dt,
acest element se deplaseaza pe distanta 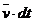 descriind suprafata elementara
descriind suprafata elementara 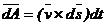 . Calculand fluxul elementar prin aceasta
suprafata, respectiv:
. Calculand fluxul elementar prin aceasta
suprafata, respectiv:  , se obtine t.e.m. sub forma:
, se obtine t.e.m. sub forma:
De
unde, integrand pe intregul circuit (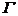 ), se obtine relatia:
), se obtine relatia:
Tinand
seama de expresiile lui  si
si 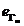 , legea inductiei electromagnetice se mai poate scrie
sub forma integrala dezvoltata:
, legea inductiei electromagnetice se mai poate scrie
sub forma integrala dezvoltata:
sau:
Forma locala a legii pentru
medii imobile are forma:
si
reprezinta cea de a doua ecuatie a lui Maxwell. Legea inductiei
electromagnetice evidentiaza o prima legatura intre
campul electric si cel magnetic:
variatia in timp a campului magnetic produce camp electric.