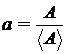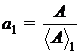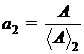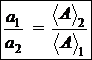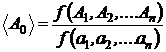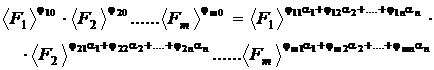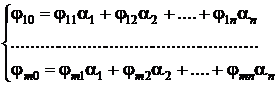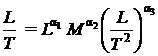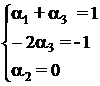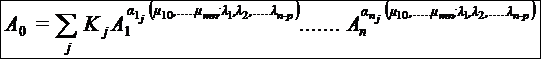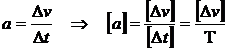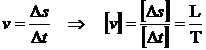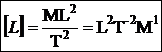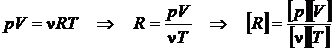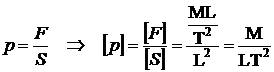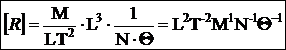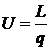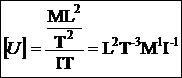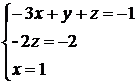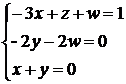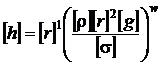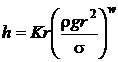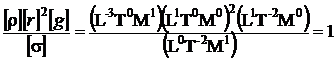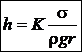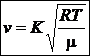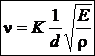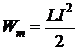MASURARE,
SISTEMUL INTERNATIONAL, ANALIZA DIMENSIONALA
 DEFINITII SI FORMULE
DEFINITII SI FORMULE
Masurare inseamna
compararea a doua marimi fizice de acelasi fel, dintre care una
este luata ca etalon. Rezultatul masurarii este un numar.
Acest numar nu poate avea o semnificatie ulterioara daca nu
este specificat si etalonul (numit in mod obisnuit "unitate de
masura". De exemplu, masurand camera cu pasul si
gasind ca acesta intra de sase ori in lungimea camerei,
informatia ca lungimea incaperii este 6 este absolut inutila
daca nu adaugam si cuvantul "pasi".
Teorema
fundamentala a unitatilor de masura afirma ca
raportul numerelor care reprezinta rezultatele masurarii unei
aceleiasi marimi fizice cu doua etaloane diferite este egal cu
inversul raportului dintre cele doua etaloane. Cunoasterea acestei
teoreme ne ajuta sa gasim valoarea pe care am determina-o
masurand cu un anumit etalon, in functie de rezultatul
masurarii cu alt etalon, doar cunoscand raportul celor doua
etaloane. De exemplu, un coleg al dumneavoastra are un monitor cu diagonala
de 21 de inch. Daca doriti sa stiti marimea
diagonalei in centimetri, nu este nevoie sa mergeti la el acasa
cu ruleta pentru a o masura personal. Este suficient sa
stiti ca 1 inch are aproximativ 2,5 cm, pentru a calcula
marimea diagonalei : 21 2,5 = 52,5 cm.
In sistemele de unitati de
masura exista marimi fizice avand etaloane a caror definire
se face in mod arbitrar. Aceste marimi fizice se numesc marimi fizice fundamentale, iar
unitatile lor de masura sunt unitatile de masura fundamentale ale sistemului
de unitati de masura. Alte marimi fizice au
unitati de masura care se definesc cu ajutorul
unitatilor de masura fundamentale. Acestea se numesc marimi fizice derivate, iar
unitatile lor de masura sunt unitati de masura derivate. In Sistemul International exista
doar sapte marimi fizice fundamentale, restul marimilor fizice
fiind marimi derivate.
Marimile fizice fundamentale ale unui sistem de
unitati de masura se mai numesc dimensiunile sistemului de unitati de masura.
Relatia care exista intre o unitate de masura derivata
si unitatile de masura fundamentale poate fi transpusa
in mod mai general ca o relatie cu dimensiunile sistemului de
unitati de masura. Aceasta relatie se
numeste formula
dimensionala.
Analiza
dimensionala este domeniul care se ocupa cu stabilirea relatiilor intre
formulele dimensionale ale diferitelor marimi fizice. Pe baza acestor
relatii se pot uneori determina forme aproximative ale unor legi valabile
in anumite situatii experimentale. Chiar daca formulele determinate
utilizand analiza dimensionala sunt doar aproximative, ele pot constitui
un mare ajutor in simplificarea experimentelor care urmeaza sa
stabileasca forma corecta a legilor respective. De asemenea, prin
analiza dimensionala se pot pune in evidenta rapoarte adimensionale
ale unor marimi fizice, numite criterii,
care sunt utilizate pentru a caracteriza preponderenta unui anumit efect
fizic in raport cu altul. De exemplu, raportul adimensional (adica
fara unitate de masura) intre densitatea unui corp si
densitatea unui lichid (rcorp rlichid) constituie un criteriu de flotabilitate. Daca
valoarea criteriului este supraunitara, corpul se scufunda complet in
lichid, iar in caz contrar, pluteste. Analiza dimensionala se
asociaza si cu o alta metodologie de lucru, denumita similitudine. Daca formulele
dimensionale care caracterizeaza un anumit proces fizic (de exemplu,
mecanic) coincid cu acelea care se refera la alt proces fizic (de exemplu,
electric), atunci prin studiul experimental al unuia dintre ele si
utilizand stiinta similitudinii se pot trage concluzii asupra
rezultatelor care s-ar obtine
studiind celalalt proces.
Metoda lui Rayleigh constituie o
modalitate relativ simpla de a stabili posibile formule matematice care
sa descrie interdependenta marimilor fizice care caracterizeaza
desfasurarea unui anumit proces fizic. In esenta, metoda
presupune ca una dintre marimile implicate in proces este un produs
de puteri necunoscute ale celorlalte marimi. Considerentele de
analiza dimensionala permit gasirea de relatii intre exponentii
(puterile) din formula, rezultatul fiind in cazul cel mai favorabil chiar
legea care guverneaza respectivul proces, determinata pana la nivelul
unei constante ce urmeaza a fi masurata experimental. Metoda
Rayleigh este eficienta mai ales in studiul unor procese fizice in care
numarul parametrilor implicati este mic, in caz contrar aplicarea ei
devenind greoaie. In situatiile mai complicate se foloseste o
alta metoda, numita teorema , care are avantajul de a fi
mai corecta din punct de vedere fizic.

ASPECTE TEORETICE
Scopul
fizicii este acela de a stabili legile in virtutea carora se
desfasoara procesele din natura. Aceste legi pot fi
exprimate atat sub forma calitativa cat si sub forma
cantitativa. Forma calitativa a unei legi fizice este de cele mai
multe ori prea vaga pentru a avea aplicatii practice. De aceea, este necesara stabilirea unei forme cantitative
pentru fiecare lege a fizicii.
Forma cantitativa a
unei legi a fizicii este o relatie matematica intre marimi fizice masurabile.
Marimile fizice masurabile sunt, asa
cum le spune si numele, acele marimi fizice care pot fi
masurate. Iata definitia masurarii : masurarea unei marimi fizice
inseamna compararea ei cantitativa cu o marime fizica de
aceeasi natura, aleasa ca unitate
de masura.
Vom
folosi in continuare urmatoarele notatii :
A = marimea fizica
masurabila
<A> = unitatea de
masura
a = valoarea numerica rezultata in
urma masurarii
Intre
aceste marimi exista urmatoarea relatie :
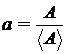
Evident,
aceeasi marime fizica poate fi masurata cu doua
unitati de masura diferite :
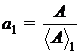 ;
; 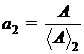
Facand raportul celor doua valori numerice, rezulta :
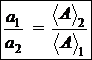
Aceasta relatie a primit denumirea de teorema fundamentala a
unitatilor de masura si se enunta astfel
: masurand o marime fizica cu doua unitati de
masura diferite, raportul valorilor numerice obtinute este
invers proportional cu raportul celor doua unitati de
masura, fiind independent de marimea fizica masurata.
Forma cantitativa
a unei legi fizice poate fi exprimata in doua moduri diferite :
formula matematica, adica relatia
matematica dintre marimile fizice :
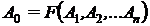
formula fizica, adica relatia
matematica dintre valorile marimilor fizice :
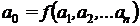
In
general, determinarea unei legi a
fizicii se face pe cale experimentala, gasindu-se corelatiile
intre valorile marimilor fizice care intervin. Aceste valori sunt stabilite utilizand unitati de
masura specifice fiecareia dintre marimile fizice implicate.
Totalitatea unitatilor de masura atasate
marimilor fizice cunoscute la un moment dat se numeste sistem de unitati de
masura.
Daca unitatile de masura
apartinand unui sistem de unitati de masura sunt
definite in mod arbitrar atunci sistemul de unitati de
masura se numeste incoerent. Folosirea unui sistem de unitati
de masura incoerent genereaza neajunsuri in ceea ce
priveste relatia dintre formulele fizica si matematica
ale unei legi a fizicii.
Eliminarea
discrepantelor intre formula fizica si cea matematica este
aceea care impune reducerea la minimum posibil a marimilor fizice care au
unitati de masura alese arbitrar.
Daca intr-un sistem de unitati de
masura numarul marimilor fizice fundamentale este cel mai
mic posibil, sistemul de unitati de masura se numeste sistem coerent de unitati de
masura.
Daca
exista N marimi fizice
distincte si n legi fizice
independente, obtinem n
relatii intre unitatile de masura ale celor N marimi fizice, numarul
marimilor fizice fundamentale devenind egal cu diferenta N - n.
Notand marimile fizice fundamentale cu :
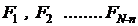
si unitatile lor de masura (stabilite
arbitrar) cu :
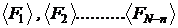
rezulta ca unitatile de masura derivate
se pot exprima ca produse ale unor anumite puteri ale unitatilor
fundamentale :
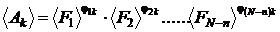
In istoria stiintei si
tehnicii s-au folosit diverse sisteme coerente de unitati de
masura. Utilizarea lor simultana putea duce la confuzii. De
aceea prin hotararea Conferintei
Generale de Masuri si Greutati (Paris, 1960) s-a
adoptat un sistem de unitati de masura unic pe plan
international, bazat pe sistemul metric. Acesta poarta denumirea de Sistemul
International de Unitati de Masura sau,
prescurtat, SI.
Sistemul International este un sistem coerent care
cuprinde sapte marimi fizice fundamentale, numite dimensiuni
ale acestui sistem de unitati.
Tabelul urmator cuprinde lista marimilor
fizice fundamentale ale Sistemului International :
|
Marimea
fizica
|
Simbolul
dimensional
|
Unitate de
masura
|
Simbolul unitatii
de masura
|
|
lungime
|
L
|
metru
|
m
|
|
timp
|
T
|
secunda
|
s
|
|
masa
|
M
|
kilogram
|
kg
|
|
temperatura
|
Q
|
kelvin
|
K
|
|
cantitate de
substanta
|
N
|
kilomol
|
kmol
|
|
intensitatea curentului electric
|
I
|
amper
|
A
|
|
intensitate luminoasa
|
E
|
candela
|
cd
|
Toate
cele sapte unitati de masura fundamentale sunt
definite in mod arbitrar (de exemplu, kelvinul este a 273,16-a parte din
intervalul de temperatura intre zero absolut si temperatura punctului
triplu al apei distilate). Toate celelalte
unitati de masura utilizate de Sistemul International
sunt unitati de masura derivate (de exemplu, viteza se
masoara in metri pe secunda).
Sistemul metric (folosit pentru prima
oara dupa Revolutia Franceza din 1789) a urmarit
exprimarea simpla a multiplilor sau submultiplilor unitatilor de
masura fundamentale. Ideea principala a fost aceea ca
multiplii sau submultiplii se precizeaza prin folosirea unor prefixe,
adaugate unitatii de masura. Aceste prefixe nominalizeaza
multiplicarea (sau demultiplicarea) prin 10 sau 1000. Iata, in continuare,
prefixele folosite la ora actuala :
|
Prefix
|
Simbol
|
Valoare
|
|
Multiplicare
|
|
Terra
|
T
|
|
|
Giga
|
G
|
|
|
Mega
|
M
|
|
|
kilo
|
k
|
|
|
hecto
|
h
|
|
|
deca
|
da
|
|
|
Unitate fundamentala
|
|
Demultiplicare
|
|
deci
|
d
|
|
|
centi
|
c
|
|
|
mili
|
m
|
|
|
micro
|
m
|
|
|
nano
|
n
|
|
|
pico
|
p
|
|
|
femto
|
f
|
|
|
atto
|
a
|
|
Omogenitatea
dimensionala a legilor fizicii, formula dimensionala a unei
marimi fizice
Fie
un de unitati de masura sistem coerent si fie 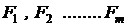 marimile fizice
fundamentale ale acestuia. Fie de asemenea formula matematica
marimile fizice
fundamentale ale acestuia. Fie de asemenea formula matematica 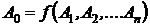 si formula
fizica
si formula
fizica 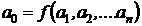 ale unei legi a
fizicii. Deoarece sistemul de unitati de masura este
coerent, forma matematica a celor doua formule este identica. In
aceasta situatie, unitatea de masura a marimii A0 se exprima astfel :
ale unei legi a
fizicii. Deoarece sistemul de unitati de masura este
coerent, forma matematica a celor doua formule este identica. In
aceasta situatie, unitatea de masura a marimii A0 se exprima astfel :
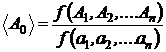
Unitatea de masura A ñ
nu
poate depinde de valorile particulare a1,
a2, an pe care le iau
marimile fizice A1, A2,. An ! Rezulta ca legea fizica 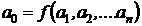 trebuie sa fie o functie omogena in raport
cu unitatile de masura ale marimilor fizice de care
depinde :
trebuie sa fie o functie omogena in raport
cu unitatile de masura ale marimilor fizice de care
depinde :
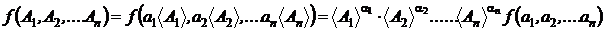
Aceasta cerinta care trebuie satisfacuta de
legea fizica se numeste conditia de omogenitate.
Daca conditia de omogenitate este satisfacuta, rezulta
:
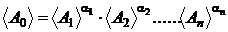
Pe de alta parte,
unitatile de masura derivate A A Anñ se
exprima in functie de unitatile fundamentale, conform
relatiilor :
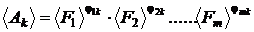
Inlocuind in relatia
rezultata din conditia de omogenitate obtinem :
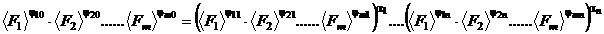
sau :
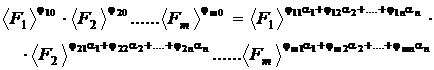
Deoarece unitatile
de masura F F Fm au
fost definite arbitrar, relatia poate fi satisfacuta doar
daca exponentii aceleiasi unitati de masura
valori egale in cei doi membri ai ecuatiei :
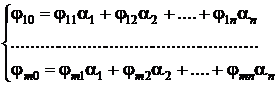
Ele sunt echivalente urmatoarei formulari a conditiei de omogenitate :
Termenii unei expresii matematice, care corespunde
unei legi a fizicii, trebuie sa aiba acelasi grad de omogenitate
in raport cu fiecare dintre unitatile de masura
fundamentale.
Conditia de
omogenitate este independenta de unitatile de masura
ale marimilor fizice fundamentale ale sistemului de unitati de
masura
Deoarece conditia de omogenitate depinde doar
de alegerea marimilor fizice fundamentale, putem introduce notiunea
de dimensiune asociata unei marimi fizice fundamentale
Fi , notata Fi
In aceste conditii, relatiilor intre
unitatile de masura derivate si unitatile de
masura fundamentale :
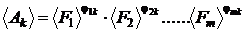
le corespund relatii
asemanatoare intre dimensiunea marimii derivate si dimensiunile
marimilor fundamentale :
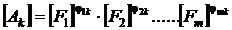
Acest tip de relatie poarta numele de formula dimensionala a unei marimi fizice.
Metoda Rayleigh
Sa presupunem
ca suntem in situatia ca trebuie sa determinam
expresia exacta a unei legi a fizicii, inca necunoscuta, de
forma :
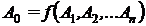
Exista o infinitate de relatii matematice posibile intre
marimile fizice A0,A1, . An. Nu toate aceste relatii matematice au si sens fizic ! Pot avea sens fizic doar expresiile care verifica conditia de
omogenitate :
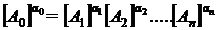
Ce avantaje ar putea rezulta
din acest fapt ? Pentru a intelege cum putem utiliza conditia de
omogenitate dimensionala, sa examinam in continuare un :
EXEMPLU
Sa consideram ca viteza v cu care atinge solul un corp
lasat liber la o inaltime h
depinde si de masa sa m si
de acceleratia gravitationala g.
Frecarile se pot neglija.
Cautam o lege a fizicii de forma :
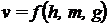
Formulele dimensionale ale marimilor care
intervin sunt :
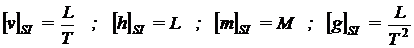
Conform conditiei de omogenitate dimensionala
avem :
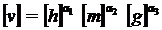
sau :
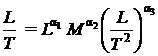
sau :
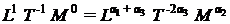
Dimensiunile sistemului de unitati de
masura sunt marimi independente, ceea ce are drept urmare faptul
ca exponentii lor din membrul stang trebuie sa fie egali cu exponentii
din membrul drept al expresiei :
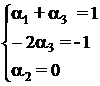
Solutiile acestui sistem de ecuatii sunt :
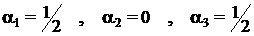
Rezulta ca relatia de omogenitate are
forma :
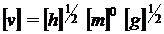
sau :
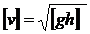
Se stie ca legea vitezei caderii
libere a unui corp in campul gravitational terestru este :
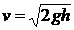
Comparand
conditia de omogenitate dimensionala cu legea vitezei, remarcam
asemanarea lor ! Diferenta este data doar de un coeficient
numeric adimensional.
Concluzia pe care o sugereaza
acest exemplu este urmatoarea :
Cel putin in anumite cazuri, expresia
matematica a unei legi a fizicii corespunde pana la unii factori
numerici adimensionali cu expresia matematica a conditiei de
omogenitate.
Desigur,
exemplul studiat a fost unul particular. In cazul general, exista urmatoarele
posibilitati :
Numarul ecuatiilor independente ale
sistemului de ecuatii, p m, este mai mare decat numarul n al exponentilor aj . In acest caz, sistemul de ecuatii
este incompatibil. Sensul fizic al
acestei situatii matematice este acela ca numarul marimilor
fizice luate in considerare este prea mic, fenomenul studiat depinzand si
de alte marimi fizice. Legea pe care o cautam 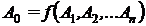 nu exista !
nu exista !
Numarul ecuatiilor independente ale
sistemului de ecuatii, p m, este egal cu numarul n
al exponentilor aj. In acest caz, sistemul de ecuatii este
compatibil determinat, iar exponentii aj sunt unic
determinati. Sensul fizic este
acela ca exista o singura relatie matematica intre
marimile fizice considerate care sa reprezinte o lege a fizicii.
Numarul ecuatiilor independente ale
sistemului de ecuatii, p m, este mai mic decat numarul n al exponentilor aj . In acest caz, sistemul de ecuatii
este compatibil nedeterminat. Dintre exponentii aj , p se exprima in functie de
ceilalti (n - p) exponenti, luati ca
parametri. Sensul fizic este ca
exista mai multe expresii matematice compatibile cu legea fizica cautata.
Rayleigh si-a propus
sa determine forma concreta a legii fizice in cazurile al doilea
si al treilea. Pentru aceasta el face urmatoarea afirmatie
suplimentara :
Ipoteza lui Rayleigh omogenitatea in
raport cu dimensiunile marimilor fizice este o consecinta a
omogenitatii in raport cu insasi marimile fizice ce intervin
in expresia unei legi fizice.
Matematic aceasta ipoteza se poate exprima astfel :
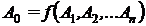 T
T
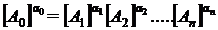 T
T
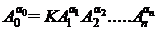
unde K este o constanta
numerica ( K
In cazul al doilea, aceasta
ipoteza, ne permite sa afirmam ca legea fizica cautata are o forma unica :
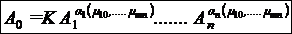
In cazul al treilea, in functie de
rangul nedeterminarii, (n - p), se vor introduce parametrii l l ln-p, astfel incat
solutiile sistemului de ecuatii sunt de forma :
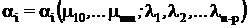
Conform ipotezei lui Rayleigh, rezulta :
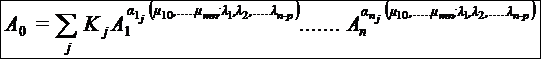
adica A0
reprezinta o suma finita
sau infinita de expresii matematice compatibile cu legea fizica
ceruta, diferind una de cealalta prin valorile parametrilor l. Valorile parametrilor Kj
si l , precum si numarul de termeni ai sumei
urmeaza sa se stabileasca pe cale experimentala.
In
final, putem face urmatoarele observatii asupra metodei lui Rayleigh :
Ea reprezinta o cale lesnicioasa pentru
determinarea expresiei matematice a unor legi fizice simple, care depind de un
numar redus de parametri. Dificultatea de a o utiliza creste
odata cu marirea numarului de parametri fizici implicat de legea
cautata. Ipoteza lui Rayleigh privind omogenitatea legilor fizicii nu
este valabila in toate cazurile si de aceea solutiile pe care le
obtinem sunt uneori eronate sau incomplete.
ALTE EXEMPLE
Determinati
formula dimensionala a lucrului mecanic.
Rezolvare
Formula de
definitie a lucrului mecanic este :
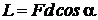
Prin urmare, formula dimensionala este :
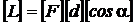
Dimensiunea deplasarii d
este lungime L, iar functia cosinus este adimensionala: cos a = 1. Pentru a gasi
dimensiunea fortei, vom utiliza principiul fundamental al dinamicii :
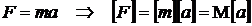
Folosind definitiile acceleratiei si vitezei, mai
obtinem :
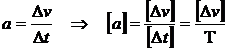
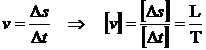
Rezulta :
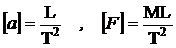
In final :
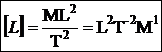
Determinati
formula dimensionala a constantei gazelor perfecte.
Rezolvare
Vom porni de la
ecuatia de stare a gazului ideal :
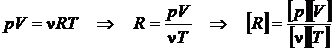
Dar :
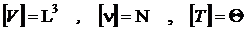
iar :
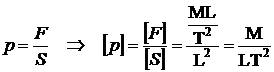
Rezulta
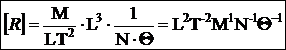
Determinati
formula dimensionala a tensiunii electrice.
Rezolvare
Formula de
definitie a tensiunii electrice este :
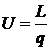
unde L este lucrul mecanic
facut de campul electric la deplasarea sarcinii q. Sarcina electrica poate fi definita in functie de
intensitatea curentului electric :
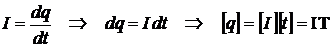
Rezulta :
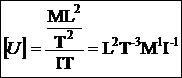
Utilizati metoda Rayleigh pentru a determina formula
presiunii hidrostatice.
Rezolvare
Presiunea
hidrostatica depinde de densitatea r si adancimea h ale lichidului, precum si de
acceleratia gravitationala g.
Putem scrie :
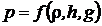
Conform conditiei de omogenitate dimensionala, putem scrie :
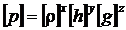
Substituind cu formulele dimensionale corespunzatoare,
rezulta :
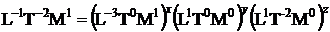
De aici :
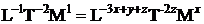
Prin egalarea exponentilor celor trei dimensiuni, obtinem :
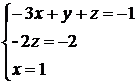
Solutiile acestui sistem de ecuatii sunt x = 1, y = 1 si z = 1. Prin urmare, conditia de
omogenitate dimensionala se scrie astfel :
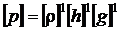
Conform ipotezei facute de Rayleigh, conditia de omogenitate
ar reflecta chiar legea cautata :
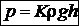
K fiind un coeficient numeric
adimensional care urmeaza sa fie determinat pe cale
experimentala.
Utilizati
metoda Rayleigh pentru a determina inaltimea h la care urca un lichid de densitate r intr-un tub capilar de
raza r. Coeficientul de tensiune
superficiala al lichidului este s si se
masoara in N/m, iar acceleratia gravitationala este g. Se stie ca
inaltimea este invers proportionala cu raza tubului
capilar.
Rezolvare
Inaltimea ceruta depinde de
densitatea r si
coeficientul de tensiune superficiala s ale lichidului, de raza
tubului capilar r, precum si de
acceleratia gravitationala g.
Putem scrie :
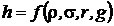
Conditia de omogenitate dimensionala este :
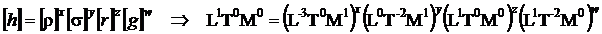
Se formeaza sistemul de ecuatii :
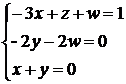
Acesta este un sistem compatibil simplu nedeterminat. Va trebui ca una
dintre necunoscute sa fie luata ca parametru. Fie aceasta w. Solutiile sunt x = w,
y = -w si z = 1 + 2w. Prin urmare, conditia de
omogenitate dimensionala se scrie astfel :
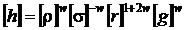
Putem scrie si :
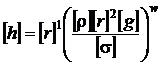
Conform ipotezei lui Rayleigh :
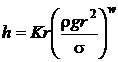
Cantitatea continuta in paranteza este un complex
adimensional. In adevar :
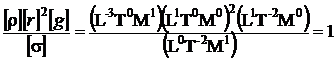
In general, fiecarei variabile luata ca parametru ii corespunde
cate un complex adimensional.
Daca folosim
si informatia oferita de enunt, rezulta ca
exponentul 1 + 2w al razei
capilarului trebuie sa aiba valoarea -1. Rezulta w = -1 si :
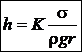
Utilizati metoda
Rayleigh pentru a gasi relatia de legatura intre viteza
termica a moleculelor unui gaz, masa molara a gazului, temperatura
gazului si constanta gazelor ideale.
Rezolvare
Conditia de
omogenitate dimensionala este :
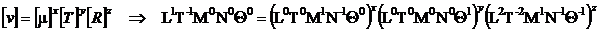
Solutiile sunt x = -1/2, y = 1/2 si z = 1/2.
Conform ipotezei lui Rayleigh :
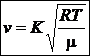
Utilizati metoda
Rayleigh pentru a gasi frecventa de oscilatie n a unei placute de
cuart in functie de grosimea d
a placutei, de densitatea cuartului r si de modulul de
elasticitate E (care se
masoara in N/m2).
Rezolvare
Conditia
de omogenitate dimensionala este :
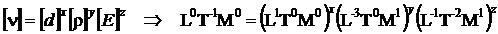
Solutiile sunt x = -1, y = -1/2 si z = 1/2.
Prin urmare, conditia de omogenitate dimensionala se scrie astfel :
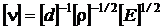
Conform ipotezei lui Rayleigh :
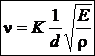

TEMA
Determinati formula
dimensionala a inductantei electrice.
Indicatie
Energia campului
magnetic al unui curent electric are formula
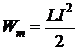
Determinati
formula dimensionala a inductiei magnetice.
Indicatie
Forta electromagnetica
are expresia
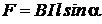
Un
corp se roteste uniform pe o traiectorie circulara de raza r. Viteza unghiulara a
rotatiei este w. Folositi
metoda Rayleigh pentru a afla forta centripeta.
Utilizati
metoda Rayleigh pentru a gasi relatia de legatura intre putere,
forta si viteza.
Utilizati
metoda Rayleigh pentru a determina timpul de urcare al unui corp aruncat
vertical in sus.
Utilizati metoda Rayleigh pentru
a determina viteza initiala v
a unui autoturism care franeaza cu acceleratia a pana la oprire.
Utilizati metoda
Rayleigh pentru a gasi relatia de legatura intre putere,
intensitatea curentului electric si tensiunea electrica.
Utilizati metoda
Rayleigh pentru a gasi relatia de legatura intre fluxul de
inductie magnetica, inductanta si intensitatea
curentului electric.