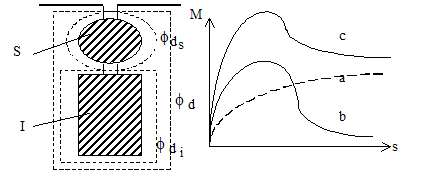Masina asincrona
1 Elemente constructive
de baza


Masina asincrona are in
principal doua parti constructive:
statorul, partea imobila care cuprinde miezul feromagnetic, carcasa cu
talpile de prindere, infasurarea statorica, cutia de borne;
rotorul, partea mobila care cuprinde miezul feromagnetic rotoric,
infasurarea rotorica, arborele masinii.
Miezul statoric este realizat din tole de otel electrotehnic, izolate cu lac, stranse
in pachet rigid si fixat in carcasa masinii. Miezul are forma
cilindrica, la periferia interioara a acestuia fiind practicate
crestaturi distribuite uniform. In crestaturi sunt plasate spirele
unei infasurari trifazate.
Infasurarea
statorica este alcatuita din trei
infasurari de faza identice, decalate la periferia interioara
cu unghiul geometric 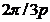 una fata de
celelalta. Acestea sunt conectate intre ele in stea sau triunghi si
legate la o sursa trifazata de c. a. prin intermediul unei cutii de
borne statorice. Spirele realizate din conductor de Cu izolat, sunt izolate
fata de peretii crestaturii. Infasurarile se
impregneaza cu lac pentru rigidizare, o mai buna izolare
electrica si conductie termica.
una fata de
celelalta. Acestea sunt conectate intre ele in stea sau triunghi si
legate la o sursa trifazata de c. a. prin intermediul unei cutii de
borne statorice. Spirele realizate din conductor de Cu izolat, sunt izolate
fata de peretii crestaturii. Infasurarile se
impregneaza cu lac pentru rigidizare, o mai buna izolare
electrica si conductie termica.
Miezul rotoric are forma cilindrica si este realizat din tole de otel
electrotehnic, uneori izolate intre ele. La periferia miezului sunt practicate
crestaturi in care se plaseaza infasurarea rotorica.
Miezul este strans rigid si solidarizat cu arborele rotoric.
Infasurarea
rotorica poate fi realizata in doua moduri:
infasurarea
trifazata realizata din trei infasurari monofazate,
decalate la periferia rotorului cu unghiul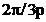 alcatuite din bobine plasate in crestaturi si
conectate in stea; capetele libere sunt legate fiecare la cate un inel din
material conductor, iar inelele se izoleaza intre ele si
fata de arborele rotoric, dar se rotesc odata cu acesta; pe
fiecare inel calca cate o perie de bronz-grafit; cele trei perii sunt
legate apoi la trei borne plasate in cutia de borne a rotorului; sistemul de
inele si perii asigura contactele alunecatoare intre
infasurarea rotorica si exteriorul masinii;
rezulta astfel un rotor bobinat;
alcatuite din bobine plasate in crestaturi si
conectate in stea; capetele libere sunt legate fiecare la cate un inel din
material conductor, iar inelele se izoleaza intre ele si
fata de arborele rotoric, dar se rotesc odata cu acesta; pe
fiecare inel calca cate o perie de bronz-grafit; cele trei perii sunt
legate apoi la trei borne plasate in cutia de borne a rotorului; sistemul de
inele si perii asigura contactele alunecatoare intre
infasurarea rotorica si exteriorul masinii;
rezulta astfel un rotor bobinat;
infasurarea
rotorica sub forma de colivie de veverita este un ansamblu
de bare din material conductor (de obicei Al) care umple crestaturile
rotorice, scurtcircuitate la ambele capete de inele; rezulta astfel un rotor in scurtcircuit (fig. 2.11).

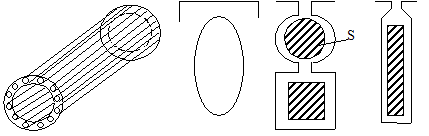
a b c d
Fig. 2.11 Rotor in colivie de veverita
(a), simpla (b),
dubla (c), cu bare
adanci (d).
Colivia poate fi simpla (fig.
2.11a, b), turnata din aluminiu, introdusa in crestaturi
rotunde sau ovale. Crestaturile pot fi: adanci (fig. 2.11d) (cu inaltimea de10-12 ori
mai mare decat latimea), in care barele adanci se executa din Cu
cu sectiune dreptunghiulara; dubla colivie (fig. 2.11c), colivia superioara S cu
rezistenta electrica relativ mare si reactanta
mica (confectionate din alama), cea inferioara I cu
rezistenta cat mai mica si reactanta mare
(confectionate din Cu).
Intrefierul este spatiul dintre stator si rotor. Cu cat acesta este mai mic
cu atat inductia magnetica este mai mare (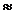 0,5 mm).
0,5 mm).
2 Regimul de motor
In regimul de motor,
masina transforma puterea electrica primita de la o
retea trifazata de c. a. in putere mecanica cedata pe la
arbore unui mecanism (masina de lucru).
Cele trei
infasurari de faza ale statorului alimentate de la un
sistem trifazat simetric de tensiuni, vor fi parcurse de curenti cu
pulsatia 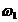 , curenti care la randul lor formeaza un sistem
trifazat simetric. Acesti curenti statorici vor produce in
intrefierul masinii un camp magnetic invartitor de excitatie, care se
roteste intr-un sens care depinde de succesiunea fazelor statorului, cu viteza
unghiulara:
, curenti care la randul lor formeaza un sistem
trifazat simetric. Acesti curenti statorici vor produce in
intrefierul masinii un camp magnetic invartitor de excitatie, care se
roteste intr-un sens care depinde de succesiunea fazelor statorului, cu viteza
unghiulara:
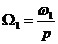 (viteza de sincronism ) (2.35)
(viteza de sincronism ) (2.35)
Campul invartitor va
induce in infasurarea trifazata a rotorului imobil 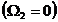 , identica cu aceea statorica, un sistem trifazat
simetric de t.e.m. de pulsatie:
, identica cu aceea statorica, un sistem trifazat
simetric de t.e.m. de pulsatie:
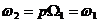 (2.36)
(2.36)
Presupunem ca
infasurarea rotorului este conectata in dubla stea; atunci
cele trei t.e.m. vor produce un sistem trifazat simetric de curenti de
aceeasi pulsatie  . Sensul succesiunii fazelor la periferia rotorului va fi dat
de sensul de rotatie al campului magnetic de excitatie. Deoarece
rotorul cu infasurarile sale, strabatute de curenti,
este situat in campul magnetic invartitor statoric, asupra acestuia se va
exercita un cuplu electromagnetic M,
in sensul succesiunii fazelor sale, identic cu sensul campului magnetic
invartitor. Daca acest cuplu este mare, astfel incat sa invinga
cuplul rezistent la arbore, rotorul se invarteste in sensul campului
statoric. Accelerarea rotorului dureaza atata timp cat cuplul dezvoltat de
masina este mai mare decat cuplul rezistent
. Sensul succesiunii fazelor la periferia rotorului va fi dat
de sensul de rotatie al campului magnetic de excitatie. Deoarece
rotorul cu infasurarile sale, strabatute de curenti,
este situat in campul magnetic invartitor statoric, asupra acestuia se va
exercita un cuplu electromagnetic M,
in sensul succesiunii fazelor sale, identic cu sensul campului magnetic
invartitor. Daca acest cuplu este mare, astfel incat sa invinga
cuplul rezistent la arbore, rotorul se invarteste in sensul campului
statoric. Accelerarea rotorului dureaza atata timp cat cuplul dezvoltat de
masina este mai mare decat cuplul rezistent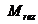 .
.
Presupunem ca
rotorul a ajuns in regim stationar si se invarteste cu viteza
uniforma 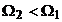 . Viteza relativa a campului invartitor de
excitatie este
. Viteza relativa a campului invartitor de
excitatie este 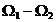 , iar pulsatia t.e.m. induse si a curentilor
din fazele rotorului este:
, iar pulsatia t.e.m. induse si a curentilor
din fazele rotorului este:
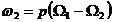 (2.37)
(2.37)
Alunecarea masinii este in acest caz:
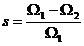 (2.38)
(2.38)
Pulsatia
curentilor rotorici este 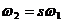 . Va apare campul magnetic invartitor de reactie, cu
aceeasi viteza fata de rotor ca si campul magnetic
invartitor de excitatie; cele doua campuri se compun si se
obtine campul magnetic invartitor rezultant. Sub actiunea campului
rezultant se induce intr-o faza rotorica t.e.m. rezultanta
. Va apare campul magnetic invartitor de reactie, cu
aceeasi viteza fata de rotor ca si campul magnetic
invartitor de excitatie; cele doua campuri se compun si se
obtine campul magnetic invartitor rezultant. Sub actiunea campului
rezultant se induce intr-o faza rotorica t.e.m. rezultanta 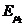 . Fie
. Fie 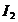 curentul rotoric de
faza. Cuplul electromagnetic care se exercita asupra rotorului este
deci:
curentul rotoric de
faza. Cuplul electromagnetic care se exercita asupra rotorului este
deci:
 (2.39)
(2.39)
Deoarece
infasurarile de faza sunt conectate in scurtcircuit,
tensiunea la bornele lor este nula, numaratorul din expresia
cuplului pune in evidenta puterea activa pierduta prin
efect Joule in infasurarile rotorului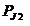 .
.
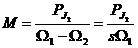 (2.40)
(2.40)
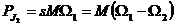
Puterea mecanica
dezvoltata de motor este:
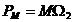 (2.41)
(2.41)

unde: 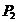 - puterea
necesara masinii de lucru;
- puterea
necesara masinii de lucru;
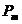 - pierderile
mecanice (frecari cu aerul si in lagare);
- pierderile
mecanice (frecari cu aerul si in lagare);
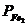 - pierderile in Fe,
in miezul feromagnetic al rotorului.
- pierderile in Fe,
in miezul feromagnetic al rotorului.
Rotorul in ansamblu
necesita puterea:
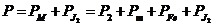 (2.42)
(2.42)
care este transmisa acestuia prin intermediul
campului electromagnetic din intrefier (putere electromagnetica). Aceasta
se mai poate exprima si sub forma:
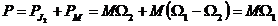 (2.43)
(2.43)
Puterea activa
primita de masina de la la retea este 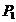 :
:
 (2.44)
(2.44)
Bilantul puterilor este reprezentat in fig. 2.12.
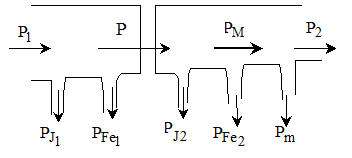
Fig. 2.12 Bilantul puterilor la motorul
asincron.
Viteza unghiulara
de rotatie 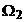 a rotorului motorului
asincron nu poate depasi viteza
a rotorului motorului
asincron nu poate depasi viteza 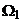 de sincronism. Daca
de sincronism. Daca 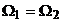 t.e.m. induse ar fi
nule si la fel curentii rotorici, iar cuplul dezvoltat ar fi M = 0, deci rotorul se va frana si
se va opri. Din acest motiv masina se numeste masina asincrona. In regim de motor, masina
functioneaza cu viteza
t.e.m. induse ar fi
nule si la fel curentii rotorici, iar cuplul dezvoltat ar fi M = 0, deci rotorul se va frana si
se va opri. Din acest motiv masina se numeste masina asincrona. In regim de motor, masina
functioneaza cu viteza  , adica pentru alunecari
, adica pentru alunecari 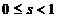 , iar in regim normal de functionare viteza
, iar in regim normal de functionare viteza  :
:
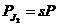
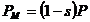 (2.45)
(2.45)
Pierderile in
infasurarile rotorice reprezinta fractiunea s din puterea electromagnetica P transmisa rotorului, in timp ce
puterea mecanica reprezinta fractiunea 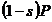 . Cum pierderile prin efect Joule sunt mult mai mici decat
puterea mecanica
. Cum pierderile prin efect Joule sunt mult mai mici decat
puterea mecanica 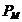 , rezulta in regim nominal o alunecare foarte mica
, rezulta in regim nominal o alunecare foarte mica 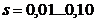 .
.
3 Ecuatiile de functionare in regim
stationar ale
motorului asincron trifazat.
Pentru stabilirea
ecuatiilor se introduc ipotezele simplificatoare:
se neglijeaza
saturatia si fenomenul de histerezis al campului magnetic;
intensitatea campului magnetic
in fier este aproximativ 0;
nu se considera armonicele
superioare ale campului invartitor;
simetrie perfecta
constructiva magnetica +electric;
viteza de rotatie a
rotorului 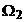 este constanta;
este constanta;
rotorul este bobinat cu
infasurarea trifazata in scurtcircuit.
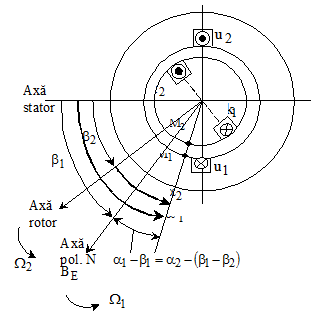
Fig. 2 13
Masina asincrona cu p
= 1.
Se
considera masina asincrona cu numarul de perechi de poli p
= 1 din fig. 2.13. Axa de simetrie a bobinei U a statorului este
considerata ca axa fixa de referinta. Axa de simetrie
a bobinei rotorice K este axa de referinta pentru rotor.
Infasurarea statorica este parcursa de sistemul trifazat
simetric de curenti 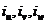 de pulsatie
de pulsatie 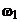 si valoarea
efectiva
si valoarea
efectiva 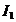 care produc campul
invartitor de excitatie
care produc campul
invartitor de excitatie 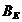 , ce se roteste cu viteza
, ce se roteste cu viteza 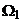 (viteza de sincronism):
(viteza de sincronism):
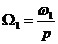 (2.46)
(2.46)
Fie 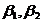 coordonatele axei
polului N al campului
coordonatele axei
polului N al campului 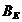 , respectiv axei de referinta a rotorului:
, respectiv axei de referinta a rotorului:
 ;
; 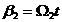 (2.47)
(2.47)
Pentru un observator 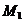 aflat pe stator la
coordonata
aflat pe stator la
coordonata 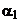 fata de axa
U, campul invartitor de excitatie are expresia:
fata de axa
U, campul invartitor de excitatie are expresia:
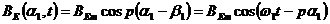 (2.48)
(2.48)
deoarece 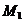 se afla la
unghiul geometric
se afla la
unghiul geometric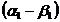 fata de axa polului N a campului.
fata de axa polului N a campului.
Pentru un observator 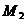 situat pe aceeasi
raza ca si
situat pe aceeasi
raza ca si 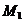 , dar pe rotor la unghiul
, dar pe rotor la unghiul 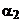 fata de axa
rotorica de referinta K, acelasi camp invartitor are
expresia:
fata de axa
rotorica de referinta K, acelasi camp invartitor are
expresia:
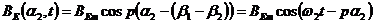 (2.49)
(2.49)
unde 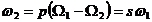 este pulsatia
marimilor electrice rotorice.
este pulsatia
marimilor electrice rotorice.
Analogia intre expresiile (2.48) si (2.49)
este evidenta. Amplitudinea in ambele cazuri este aceeasi 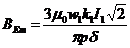 , unde k1
este coeficientul de infasurare
, unde k1
este coeficientul de infasurare 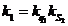 .
.
In infasurarea
rotorica se induce un sistem trifazat simetric de curenti.
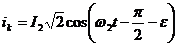 ;
;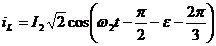 ; (2.50)
; (2.50)
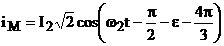
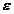 fiind defazajul
tensiune de faza, curent de faza.
fiind defazajul
tensiune de faza, curent de faza.
Sistemul de curenti
rotorici produce campul magnetic de reactie.
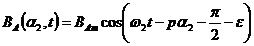 (2.51)
(2.51)
ce se roteste cu aceeasi viteza ca
si campul de excitatie dar este defazat. Valoarea a inductiei
magnetice este 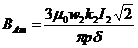 .
.
Cele doua campuri
se compun intr-un camp magnetic rezultant  ce pentru observatorul
M1 are expresia:
ce pentru observatorul
M1 are expresia:
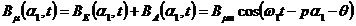 (2.52)
(2.52)
fiind defazat in urma cu unghiul 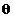 fata de
campul de excitatie.
fata de
campul de excitatie.
Consideram
curentii statorici fictivi ce produc acelasi camp magnetic  (camp de magnetizare):
(camp de magnetizare):
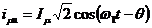 ;
;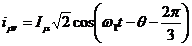 ; (2.53)
; (2.53)
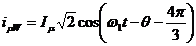
cu valoarea maxima a inductiei magnetice
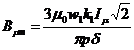 .
.
Analog se considera
curentii fictivi statorici, care produc un camp magnetic identic cu 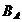 (curenti rotorici
raportati la stator).
(curenti rotorici
raportati la stator).
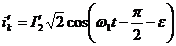 ;
;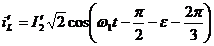 (2.54)
(2.54)
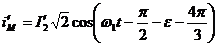
Din conditia de identitate a valorii
maxime a campului 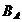 , rezulta valoarea efectiva a curentului fictiv
statoric
, rezulta valoarea efectiva a curentului fictiv
statoric 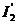 :
:
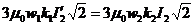
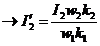 (2.55)
(2.55)
Prin introducerea sistemului de curenti de
magnetizare 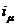 si a sistemului
de curenti rotorici raportati la stator
si a sistemului
de curenti rotorici raportati la stator 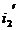 care au aceeasi pulsatie si defazaje
initiale fata de curentii statorici, respectiv egale cu
decalajele in spatiu intre campurile
care au aceeasi pulsatie si defazaje
initiale fata de curentii statorici, respectiv egale cu
decalajele in spatiu intre campurile  si
si 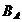 in raport cu
in raport cu 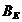 , se inlocuieste compunerea spatiala a
campurilor cu compunerea fazoriala (fig. 1.14):
, se inlocuieste compunerea spatiala a
campurilor cu compunerea fazoriala (fig. 1.14):
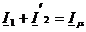
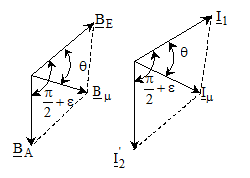
Fig. 2.14 Diagramele de fazori pentru campul
magnetic rezultant 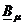
si curentul fictiv de magnetizare 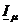 .
.
Campul invartitor
rezultant 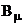 induce un sistem
trifazat simetric de t.e.m. in fazele statorului:
induce un sistem
trifazat simetric de t.e.m. in fazele statorului:
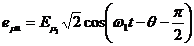 (2.56)
(2.56)
cu valoarea efectiva 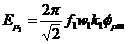 , unde
, unde 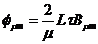 .
.
Se compara expresiile instantanee 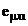 si
si  si se poate
scrie egalitatea fazoriala:
si se poate
scrie egalitatea fazoriala:
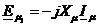 (2.57)
(2.57)
unde 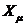 este reactanta de
magnetizare.
este reactanta de
magnetizare.
Acelasi camp
invartitor  induce t.e.m. utile
si in fazele rotorului. Pentru un observator pe rotor
induce t.e.m. utile
si in fazele rotorului. Pentru un observator pe rotor 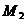 t.e.m are expresia.
t.e.m are expresia.
 , (2.58)
, (2.58)
cu valoarea efectiva 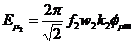 , unde
, unde  .
.
Prin analogie cu raportarea curentilor, se
raporteaza si tensiunea 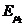 la tensiunea
la tensiunea 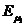 :
:
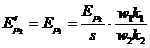 (2.59)
(2.59)
In continuare se
considera fluxurile magnetice de dispersie create de campurile magnetice
de dispersie ale infasurarii rotorice si statorice, ce
induc t.e.m. de dispersie in propriile infasurari:
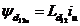 ;
;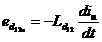 ;
;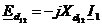 (2.60)
(2.60)
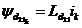 ;
;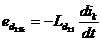 ;
;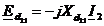
Se raporteaza marimile t.e.m rotorice la
cele statorice:
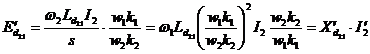
in care 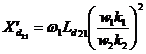 .
.
Rezulta marimea fazoriala a t.e.m
rotorice raporate la stator:
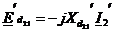 (2.61)
(2.61)
Se iau in considerare
si caderile ohmice de tensiune  :
:
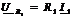
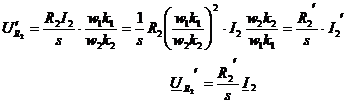 (2.62)
(2.62)
unde 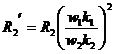 .
.
Pierderile in fier se
pot lua in considerare prin analogie cu transformatorul, considerand curentul  ce parcurge
rezistenta
ce parcurge
rezistenta 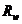 :
:
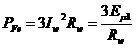 .
.
Curentul de mers in gol este, prin analogie cu
transformatorul:
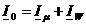
Sistemul de ecuatii
in regim stationar al motorului asincron este:
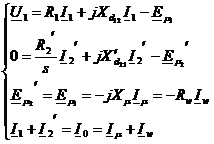 (2.63)
(2.63)
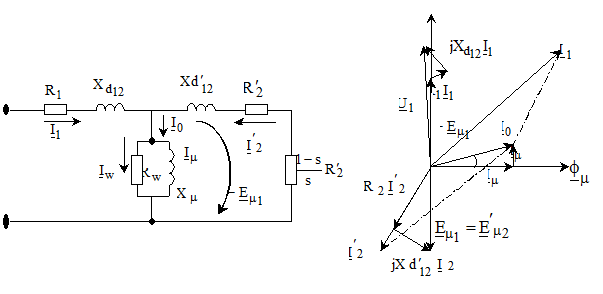
Sistemului de ecuatii (2.63) i se
asociaza schema echivalenta si diagrama de fazori din fig. 2.15.
a b
Fig. 2.14 Schema echivalenta (a), si
diagrama de fazori (b)
pentru masina asincrona.
In schema
echivalenta s-a impartit rezistenta echivalenta  a rotorului in
rezistenta
a rotorului in
rezistenta 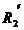 reala in care se
dezvolta pierderile Joule
reala in care se
dezvolta pierderile Joule 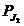 si
si 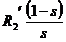 , care are semnificatia unei rezistente de
sarcina. Puterea consumata de aceasta rezistenta are
semnificatia puterii mecanice PM
dezvoltate de motor.
, care are semnificatia unei rezistente de
sarcina. Puterea consumata de aceasta rezistenta are
semnificatia puterii mecanice PM
dezvoltate de motor.
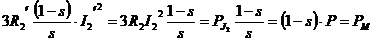
Analog cu transformatorul caderea de tensiune
pe rezistenta 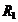 a
infasurarii statorice este foarte mica in comparatie
cu tensiunea la borne
a
infasurarii statorice este foarte mica in comparatie
cu tensiunea la borne 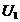 . De asemenea, caderea de tensiune datorata
dispersiilor este cateva procente din tensiunea utila
. De asemenea, caderea de tensiune datorata
dispersiilor este cateva procente din tensiunea utila 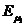 . Deci:
. Deci:
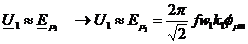
Caracteristicile motorului
asincron trifazat
a.
Caracteristica mecanica este data de
dependenta vitezei de rotatie functie de cuplul dezvoltat de
motorul asincron la tensiune de alimentare U1
si frecventa f1 constante:
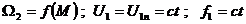
Cuplul
dezvoltat de motor este:
 (2.64)
(2.64)
Se demonstreaza ca expresia
fazoriala a curentului rotoric raportat la stator este: 
unde: 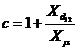 .
.
Valoarea efectiva a curentului permite
deducerea expresiei cuplului dezvoltat de motor functie de alunecare.
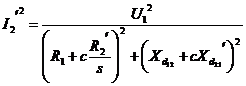
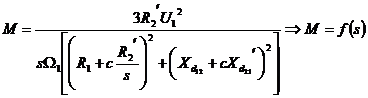
Valoarea alunecarii (alunecare critica)
pentru care se obtine valoarea maxima a cuplului este data de
ecuatia:

Se observa ca alunecarea critica
este direct proportionala cu 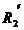 .
.
Cuplul maxim dezvoltat de motorul asincron este:
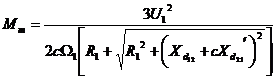 (2.65)
(2.65)
Se observa ca valoarea 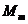 nu este dependent de
nu este dependent de 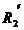 .
.
In figura 2.16 se
reprezinta functia 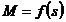 pentru
pentru 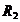 variabil.
variabil.
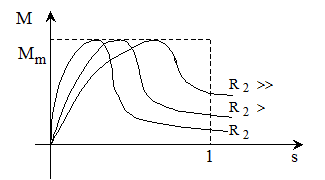
Fig. 2.16 Caracteristica mecanica
functie de rezistenta circuitului rotoric R2.
Raportul 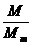 se poate exprima:
se poate exprima:
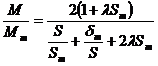 (2.66)
(2.66)
unde 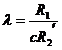 .
.
De obicei  si rezulta pentru cuplul dezvoltat M expresia:
si rezulta pentru cuplul dezvoltat M expresia:
 (formula lui Kloss) (2.67)
(formula lui Kloss) (2.67)
Facand observatii asupra formulei lui
Kloss rezulta alura curbei M(s)
din fig. 2.17:
- pentru 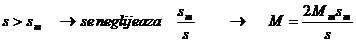 (hiperbola echilatera)
(hiperbola echilatera)
- pentru 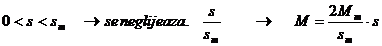 (dependenta
liniara)
(dependenta
liniara)
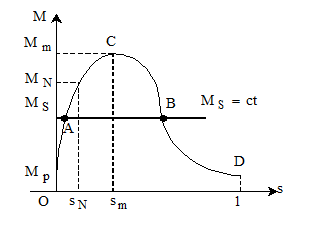
Fig. 2.17 Caracteristica mecanica M=f(s).
In
figura 2.17 se prezinta marimile cuplu critic 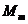 ,
, 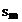 , cuplul nominal
, cuplul nominal 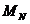 ,
, 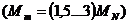 , alunecarea nominala
, alunecarea nominala 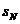 . Se observa variatia cuplului functie de
alunecare, aflata intre
. Se observa variatia cuplului functie de
alunecare, aflata intre 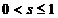 , unde s = 1 este
punctul de pornire al motorului asincron.
, unde s = 1 este
punctul de pornire al motorului asincron.
Pentru
un cuplu de sarcina 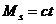 cerut de masina
de lucru, se observa ca sunt posibile doua puncte de
functionare A, B:
cerut de masina
de lucru, se observa ca sunt posibile doua puncte de
functionare A, B:
- in
punctul A daca 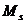 creste spre
valoarea
creste spre
valoarea  , motorul franeaza, alunecare s creste, cuplul M creste de asemenea si
franarea slabeste; rezulta noi valori pentru cuplu si
alunecare
, motorul franeaza, alunecare s creste, cuplul M creste de asemenea si
franarea slabeste; rezulta noi valori pentru cuplu si
alunecare 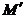 , respectiv
, respectiv 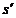 astfel incat sa
se produca egalitatea
astfel incat sa
se produca egalitatea 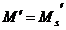 ;
;
- in
punctul B daca cuplul 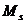 creste spre
creste spre  , motorul franeaza, alunecare s creste, cuplul M
scade si franarea se intensifica; motorul se opreste.
, motorul franeaza, alunecare s creste, cuplul M
scade si franarea se intensifica; motorul se opreste.
Rezulta ca numai portiunea de
curba liniara (OC) este stabila pentru functionarea
motorului. Punctele de pe portiunea CD sunt instabile pentru
functionarea motorului (zona instabila a curbei)
Motorul
asincron are un cuplu de pornire mic 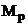
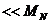 , deci nu poate porni in sarcina, cand
, deci nu poate porni in sarcina, cand 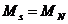 . La pornire motoarele cu motor bobinat sau cele in
simpla colivie inregistreaza un soc de curent
. La pornire motoarele cu motor bobinat sau cele in
simpla colivie inregistreaza un soc de curent 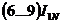 .
.
Utilizand
caracteristica 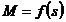 , putem trasa caracteristica mecanica:
, putem trasa caracteristica mecanica: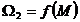 (fig. 2.18). In zona stabila de functionare (zona
liniara) variatia vitezei este
(fig. 2.18). In zona stabila de functionare (zona
liniara) variatia vitezei este  . Rezulta o caracteristica mecanica dura.
. Rezulta o caracteristica mecanica dura.
Motorul
asincron se preteaza la unele modificari constructive pentru
simplitate sau imbunatatirea performantelor sale:
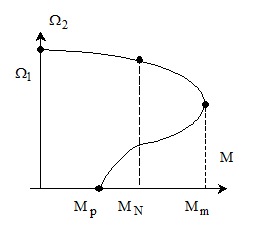
Fig. 2.18 Caracteristica
mecanica a motorului asincron.
1)
realizarea coliviei de veverita simpla pe circuitul rotoric, ce
poate fi perfect echivalata cu o infasurare trifazata
echilibrata cu parametrii cunoscuti, 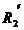 ,
, 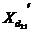 si parcursa
de curentul de faza
si parcursa
de curentul de faza 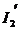 ; este simpla si robusta (fiabila) dar
prezinta dezavantajul ca nu da posibilitatea
imbunatatirii conditiilor de pornire
; este simpla si robusta (fiabila) dar
prezinta dezavantajul ca nu da posibilitatea
imbunatatirii conditiilor de pornire 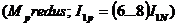 ;
;
2)
realizarea dublei colivii
-
superioara (S) cu bare de sectiune mica, cu reluctanta
mare (alama, bronz, aluminiu); 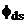 fluxul de dispersie
este mic deoarece reluctanta circuitului magnetic este mare (strabate
doua spatii de aer), rezulta reactanta Xds scazuta; aceasta este colivia de pornire (curba
a, fig. 2.19).
fluxul de dispersie
este mic deoarece reluctanta circuitului magnetic este mare (strabate
doua spatii de aer), rezulta reactanta Xds scazuta; aceasta este colivia de pornire (curba
a, fig. 2.19).
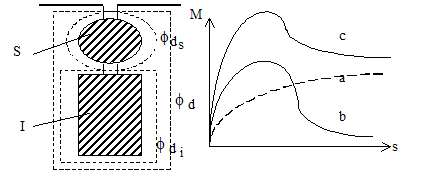
Fig. 2.19 Caracteristica mecanica pentru motorul asincron
cu rotor cu colivie dubla.
- inferioara (I) cu
reluctanta mica (bare de Cu cu sectiune mare); fluxul de
dispersie 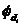 este mare si
reactanta este mare; aceasta este colivia de lucru (curba b, fig.
2.18).
este mare si
reactanta este mare; aceasta este colivia de lucru (curba b, fig.
2.18).
Modul
de functionare al motorului cu dubla colivie este:
- la
pornire 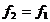 , curentul din colivia superioara este in faza cu
tensiunea (reactanta
, curentul din colivia superioara este in faza cu
tensiunea (reactanta 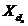 este mica),
colivia superioara produce cuplul maxim
este mica),
colivia superioara produce cuplul maxim 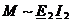 ; curentul din colivia. inferioara este defazat
perpendicular pe tensiune (reactanta
; curentul din colivia. inferioara este defazat
perpendicular pe tensiune (reactanta  este mare) si nu
produce cuplu;
este mare) si nu
produce cuplu;
- in
regim normal de functionare frecventa f2 este mult mai mica decat frecventa f1, in ambele colivii
curentul este in faza cu tensiunea, dar curentul din colivia
superioara este foarte mic, deoarece rezistenta sa este mare; cuplul
este produs de colivia inferioara.
Insumand cuplul
dezvoltat de motor in ambele colivii, curbele (a) si (b) , rezulta
caracteristica mecanica (c).
realizarea rotorului cu bare
adanci construit din barele de cupru cu inaltime mult mai mare ca
grosimea care se comporta similar cu rotorul in dubla colivie,
rezultand imbunatatirea conditiilor de pornire ale
motorului si o curba a caracteristicii mecanice identica cu cea
rezultanta in fig. 2.19.
b.
Caracteristica randamentului este data de
dependenta randamentului functie de puterea utila, la tensiune
de alimentare si frecventa constanta:

Expresia randamentului
motorului este (fig. 2.20):
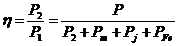 (2.68)
(2.68)
Pierderile
mecanice Pm datorate
frecarilor rotorului si ventilatorului cu aerul si in
lagare sunt functie de viteza de rotatie care este
constanta, deci sunt constante. Pierderile in fier depind de 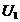 si
si 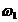 , care sunt constante si deci sunt constante. Pierderile
Joule sunt sensibil legate de sarcina motorului.
, care sunt constante si deci sunt constante. Pierderile
Joule sunt sensibil legate de sarcina motorului.
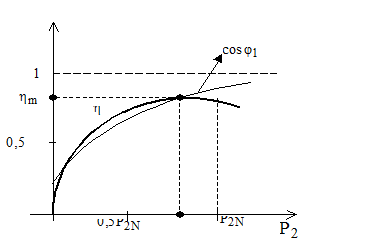
Fig. 2.20
Caracteristicile randamentului si factorului de putere.
Reprezentarea
caracteristicii se face prin analogie cu aceeasi caracteristica a
transformatorului. Randamentul 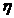 creste cu
cresterea sarcinii
creste cu
cresterea sarcinii 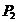 , atingand valoarea maxima
, atingand valoarea maxima 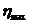 la
la 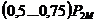 . Valorile randamentului functie de puterea
mecanica sunt:
. Valorile randamentului functie de puterea
mecanica sunt:
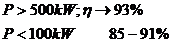

Maximul randamentului se realizeaza
odata cu egalitatea: 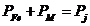 .
.
c. Caracteristica factorului de putere este data de dependenta factorului de putere de puterea
utila la tensiune si frecventa de alimentare
constanta:
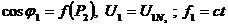 .
.
Motorul asincron
absoarbe de la reteaua de alimentare un curent defazat totdeauna in urma
tensiunii aplicate pe faza in regim simetric echilibrat(deoarece trebuie
sa absoarba o putere reactiva Q necesara magnetizarii circuitului). Deci motorul
functioneaza ca o bobina inductiva. (cu cos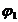 inductiv).
inductiv).
La mersul in gol
factorul de putere este mic  , deoarece puterea activa absorbita este foarte
redusa (egala cu pierderile masinii), dar puterea reactiva
este practic aceeasi ca si in plina sarcina.
, deoarece puterea activa absorbita este foarte
redusa (egala cu pierderile masinii), dar puterea reactiva
este practic aceeasi ca si in plina sarcina.
La mersul in
sarcina, puterea ceruta creste si puterea activa
absorbita de la retea creste, in timp ce puterea reactiva
ramane practic aceeasi. Factorul de putere se
imbunatateste  , cand puterea ajunge la valoarea nominala
, cand puterea ajunge la valoarea nominala 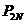 .
.
Factorul de putere
scazut la sarcini reduse este un dezavantaj important al motorului
asincron, ceea ce face sa se adopte masuri pentru
imbunatatirea factorului de putere (baterii de condensatoare,
compensatoare sincrone).




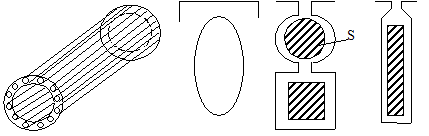


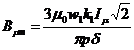 .
.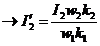

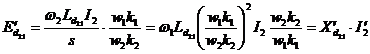
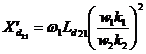 .
.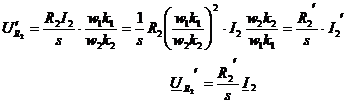
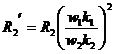 .
.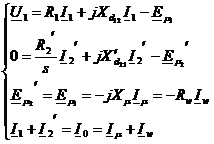



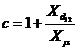 .
.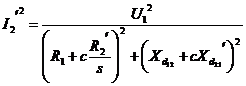
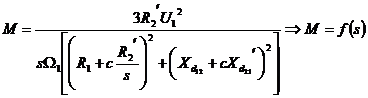

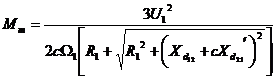

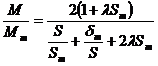
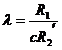 .
. (formula lui Kloss) (2.67)
(formula lui Kloss) (2.67)