METODELE
ANALIZEI CANTITATIVE
ANALIZA CANTITATIVA
= se realizeaza in baza unor metode si procedee specifice, utilizind
modele economico-financiare adecvate
1 METODA BALANTIERA
= poarta numele de "model
structural" deoarece sunt scoase in evidenta elementele componente
ale fenomenului economico-financiar analizat
=
aplicabila in cazul unor modele de tip aditiv (intre elamentele a, b, c
exista numai plus, numai minus, sau si plus si minus), care presupun studierea fenomenului
economico-financiar dupa o relatie de forma :
F = a + b - c
F
= fenomenul economico-financiar analizat; a, b, c = elemente
La timpul t0 , F0 = a0 + b0
- c0
La timpul t1 , F1 = a1 + b1
- c1
A-ANALIZA
FENOMENULUI ECONOMICO-FINANCIAR IN MARIMI ABSOLUTE ESTE :
DF = F1
- F0
scris analitic : DF = (a1 + b1
- c1) - (a0 + b0 - c0) T obtin o anumita
valoare
Din care :
1-variatia fenomenului economico-financiar
"F" in raport cu elementul "a" este :
DF(a) = (a1 + b0
- c0) - (a0 + b0 - c0) = a1 - a0
T ne arata
influenta pe care o exercita elementul "a" asupra fenomenului
economico-financiar "F" analizat
2-variatia fenomenului economico-financiar
"F" in raport cu elementul "b" este :
DF(b) = (a0 + b1
- c0) - (a0 + b0 - c0) = b1 - b0
T ne arata influenta
pe care o exercita elementul "b" asupra fenomenului economico-financiar
"F" analizat
3-variatia fenomenului economico-financiar
"F" in raport cu elementul "c" este :
DF(c) = (a0 + b0
- c1) - (a0 + b0 - c0) = -c1
+ c0
T ne arata
influenta pe care o exercita elementul "c" asupra fenomenului
economico-financiar "F" analizat
Verificam corelatia : DF = DF(a) + DF(b) + DF(c)
Un
asemenea model se utilizeaza foarte des in analiza unei structuri de
productie, structuri de activ, sau in cazul analizei financiare pe baza
bilantului contabil si a contului de profit si pierderi.
Daca avem "n" elemente formula de calcul va fi : F = a1 + a2 + a3
+..+ an = 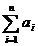
EXEMPLU : Folosim datele din
tabelul urmator :
Anul 0 = anul anterior sau ceea ce ne-am
planificat
Anul 1 = anul curent sau ceea ce am realizat
Modelul structural este:
F = a + b - c
Variatia lui "F" presupune:
DF = F1 - F0
= - 2 - 10 = - 12 unitati de masura,
T fenomenul
economico-financiar a variat din anul anterior pina in anul curent cu
(-12) unitati de masura
Din care :
1) Ca urmare a influentei factorului "a":
DF (a) = a1 - a0
= 5 - 4 = 1
2) Ca urmare a influentei elementului "b":
DF (b) = b1 - b0
= 3 - 8 = - 5
3) Ca urmare a influentei elementului "c":
DF (c) = - c1 + c0
= - 10 + 2 = - 8
Verificam corelatia : DF = DF (a) + DF (b) + DF (c)
-
12 = 1 - 5 - 8
B-ANALIZA
FENOMENULUI ECONOMICO-FINANCIAR IN MARIMI RELATIVE (PROCENTUALE) ESTE
F = a + b - c ,
La timpul t0 : F0 = a0 + b0 - c0
,
La timpul t1 : F1 = a1
+ b1 - c1 ,
DF % = 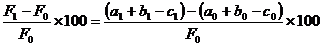
Din care :
1-variatia fenomenului economico-financiar
"F" in raport cu elementul "a" este :
DF % (a) = 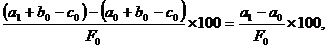
T ne arata
influenta pe care o exercita elementul "a" asupra fenomenului
economico-financiar "F" analizat.
2-variatia fenomenului economico-financiar
"F" in raport cu elementul "b" este :
DF % (b) =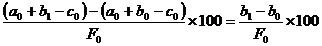 ,
,
T ne arata
influenta pe care o exercita elementul "b" asupra fenomenului
economico-financiar "F" analizat.
3-variatia fenomenului economico-financiar
"F" in raport cu elementul "c" este :
DF % (c) =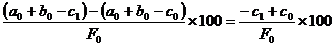 ,
,
T ne arata
influenta pe care o exercita elementul "c" asupra fenomenului
economico-financiar "F" analizat.
Se verifica apoi relatia de egalitate : DF % = DF % (a) + DF % (b) + DF % (c)
EXEMPLU : Folosim datele din
tabelul urmator :
Anul 0 = anul anterior sau ceea ce ne-am
planificat
Anul 1 = anul curent sau ceea ce am realizat
Modelul structural este:
F = a + b - c
Variatia lui "F" este:
DF = F1 - F0
= - 2 - 10 = - 12 unitati de masura
T fenomenul
economico-financiar a variat din anul anterior pina in anul curent cu
(-12) unitati de masura, ceea ce procentual inseamna:
DF % = 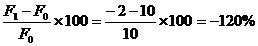 ,
,
Din care :
DF % (a) = 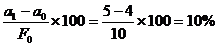 ,
,
DF % (b) =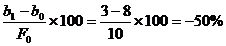 ,
,
DF % (c) =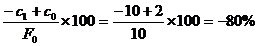 .
.
Verificam corelatia : DF % = DF % (a) + DF % (b) + DF % (c)
-120% = 10% + (-50) + (-80%)
2-METODA
SUBSTITUIRILOR IN LANT
=
una din cele mai utilizate metode in analiza economico-financiara;
=
se aplica in cazul unui produs sau raport de factori;
=
modelele utilizate sint de tip multiplicativ;
=
pentru aceasta este necesara o analiza calitativa a fenomenului,
punind in evidenta, in mod corect, relatiile de
dependenta sau de cauzalitate dintre factori si fenomenul
economico-financiar analizat;
=
se foloseste atunci cind analiza se realizeaza :
1) in marimi absolute
2)
in marimi relative
Aplicarea
corecta a acestei metode presupune respectarea a 3 criterii esentiale, si anume :
1
- substituirea factorilor se realizeaza in ordinea urmatoare :
a)
- factori cantitativi;
b)
- factori de structura (structurali);
c)
- factori calitativi.
2
- substituirea factorilor are loc in mod succesiv si nu simultan;
3
- un factor o data substituit, ramine in aceasta pozitie
(ipostaza) in toate celelalte etape de calcul.
A-METODA
SUBSTITUIRILOR IN LANT IN CAZUL UNUI PRODUS DE FACTORI
1. IN
MARIMI ABSOLUTE
ETAPA 1 - consideram ca fenomenul
economico-financiar este descris de modelul :
F
= a x b x c x d, unde a, b,
c, d = factori
ETAPA 2 - corespunzator acestui model, ii
atasam o schema factoriala :
Din schema rezulta ca fenomenul
economico-financiar "F" este influentat direct de 4 factori. Pentru
simplificarea noastra, ei sint de aceeasi natura, deci
substituirea se va face in ordinea in care apar in relatie.
ETAPA 3 - determinarea influentelor (sau
actiunii factorilor):
La timpul t0 : F0 =
a0 x b0 x c0 x d0
La timpul t1 : F1 =
a1 x b1 x c1 x d1
Variatia lui "F" este :
DF = F1 - F0
= a1 b1 c1 d1 - a0 b0
c0 d0
T obtin o anumita
variatie (pozitiva sau negativa)
Din care :
DF (a) = a1 b0 c0
d0 - a0 b0 c0 d0 =
(a1 - a0) b0
c0 d0,
T ne arata
influenta pe care o exercita factorul "a" asupra fenomenului
economico-financiar "F" analizat;
DF (b) = a1 b1
c0 d0 - a1 b0 c0 d0
= a1 (b1 - b0)
c0 d0,
T ne arata
influenta pe care o exercita factorul "b" asupra fenomenului
economico-financiar "F" analizat;
DF (c) = a1 b1
c1 d0 - a1 b1 c0 d0
= a1 b1 (c1
- c0) d0,
T ne arata
influenta pe care o exercita factorul "c" asupra fenomenului
economico-financiar "F" analizat;
DF (d) = a1 b1
c1 d1 - a1 b1 c1 d0
= a1 b1 c1
(d1 - d0),
T ne arata
influenta pe care o exercita factorul "d" asupra fenomenului
economico-financiar "F" analizat.
ETAPA 4 - se verifica daca este
respectata corelatia :
DF = DF (a) + DF (b) + DF (c) + DF (d), unde DF = variatia totala
EXEMPLU : Consideram datele
din tabelul de mai jos :
ETAPA 1 : Modelul
factorial este : F = a x b x c x d
ETAPA 2 - Schema factoriala (este cea
prezentata anterior)
La timpul t0 F0 = 8 x 15 x 20x 4 = 9.600 u.m (unitati de masura)
La timpul t1 F1 = 12 x 10 x 22 x 5 = 13.200 u.m.
T fenomenul
economico-financiar "F" a inregistrat o crestere fata de anul
anterior:
DF = F1 - F0
= 13.200 - 9.600 = 3.600 u.m.
ETAPA 3 - Determinam influentele
factoriale (vrem sa vedem masura cu cit a contribuit fiecare factor)
:
DF (a) = (a1 -
a0) b0 c0 d0 = (12 - 8) x 15 x 20 x
4 = 4.800 u.m.
T factorul "a" a
influentat pozitiv variatia fenomenului economico-financiar "F";
DF (b) = a1(b1
- b0) c0 d0 = 12 (10 - 15) x 20 x 4 = - 4.800
u.m
T factorul "b"a
influentat negativ variatia fenomenului economico-financiar "F";
DF (c) = a1b1
(c1 - c0) d0 = 12 x 10 (22 - 20) x 4 =
960 u.m.
T factorul "c"
influenteaza pozitiv, deci contribuie la cresterea fenomenului
economico-financiar "F";
DF (d) = a1 b1
c1(d1 - d0) = 12 x 10 x 22 (5 - 4) = 2.640
u.m.
T factorul "d"
influenteaza pozitiv variatia fenomenului economico-financiar
"F"
ETAPA 4 - Verificam corelatia : DF = DF (a) + DF (b) + DF (c) +DF (d)
3.600 = 4.800 - 4.800 + 960 + 2.640 T 3.600
= 3.600
ETAPA 5 - Rescriem schema factoriala
completa privind determinarile :


ETAPA 6 - CONCLUZII (analiza rezultatelor)
Fata
de anul anterior, fenomenul economico-financiar "F" a inregistrat o
crestere de 3.600 u.m., adica de 1,375 ori ( 13.200 : 9.600 = 1,375).
Aceasta crestere s-a datorat actiunii a patru factori cu
influenta directa : a, b, c, d. Dintre cei patru factori, trei
au influentat pozitiv variatia fenomenului economico-financiar "F"
(a, c, d), ceea ce inseamna ca au contribuit la cresterea
acestuia, iar unul (b) a influentat negativ variatia fenomenului
economico-financiar "F", ceea ce inseamna ca a contribuit la
diminuarea lui.
In
raport cu semnificatia fenomenului economico-financiar, influentele
celor patru factori au fost favorabile sau nefavorabile.
2. IN
MARIMI RELATIVE
Consideram ca fenomenul
economico-financiar este descris de modelul :
F = a x b x c x d
La timpul t0, F0 = a0 b0 c0 d0
La timpul t1, F1 = a1 b1 c1 d1
Variatia procentuala a lui "F" este :
DF % = 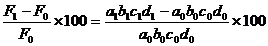 ,
,
Din care :
DF % (a) = 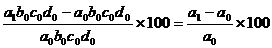 ,
,
DF % (b) =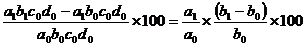 ,
,
DF % (c) = 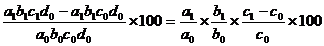 ,
,
DF % (d) = 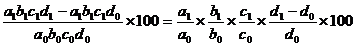 .
.
Verificam corelatia : DF % = DF % (a) + DF % (b) + DF % (c) + DF % (d)
EXEMPLU : Consideram datele
din tabelul de mai jos :
ETAPA 1 : Modelul
factorial este : F = a x b x c x d
ETAPA 2 - Schema factoriala (prezentata
anterior)
La timpul t0 , F0 =
8 x 15 x 20x 4 = 9.600 u.m (unitati de masura)
La timpul t1 , F1 =
12 x 10 x 22 x 5 = 13.200 u.m.
T fenomenul economico-financiar
"F" a inregistrat o crestere din anul anterior
DF = F1 - F0
= 13.200 - 9.600 = 3.600 u.m.
ETAPA 3 - Determinam influentele
factoriale:
DF % = 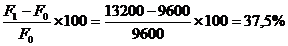
Din care :
DF % (a) = 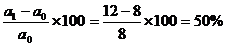
DF % (b) =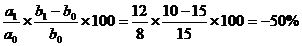
DF % (c) =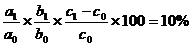
DF % (d) =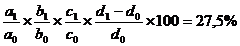
ETAPA 4 - Verificam corelatia : DF % = DF %(a) + DF %(b) + DF %(c) + DF %(d)
37,5% = 50% + (-50%) + 10% + 27,5 %
T 37,5%
=37,5%
Regula = Influenta
procentuala a actiunii factorilor are acelasi semn,intensitate
si sens ca influenta in marime absoluta a acelorasi
factori.
B - METODA
SUBSTITUIRILOR IN LANT IN CAZUL UNUI RAPORT DE FACTORI
Consideram ca fenomenul
economico-financiar este descris de modelul :
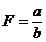
1. IN
MARIMI ABSOLUTE
a) FACTORUL
CANTITATIV SE AFLA LA NUMARATOR
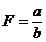 ;
; 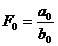 ,
, 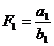
Variatia fenomenului este:
DF = F1 - F0
=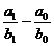
Din care:
DF (a) =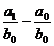 ;
;
∆F(b) = 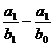 ;
;
Verificam corelatia:
F = ∆F(a) + ∆F(b)
EXEMPLU - Consideram datele
din tabelul de mai jos :
ETAPA 1 - Consideram ca F este dat de raportul : 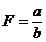 ;
;
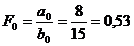 ;
;
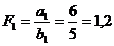
DF = F1 - F0
= 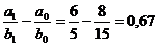
Din care :
DF(a) = 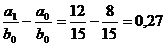
DF(b) = 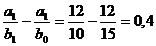
Verificam corelatia : DF = DF(a) + DF(b)
T 0,67 = 0,67
T factorii "a" si
"b" au influentat pozitiv
cresterea fenomenului economico-financiar "F", contributia cea mai
mare avind-o factorul "b"
b) FACTORUL CANTITATIV SE AFLA LA NUMITOR
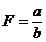 ;
; 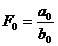 ,
, 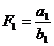
Variatia fenomenului este:
DF = F1 - F0
= 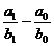
Din care :
DF (b) = 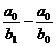 ;
;
∆F(a) = 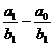
Verificam corelatia : DF = DF (b)
+ DF (a)
Schema factoriala este :
T avem doi factori cu actiune
directa care influenteaza fenomenul economico-financiar "F" .
EXEMPLU : Folosim aceleasi
date ca si in exemplul anterior.
DF = F1 - F0
=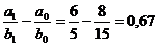 ;
;
Din care :
DF(b) = 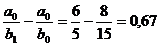
DF(a) = 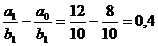
Verificam corelatia : DF = DF(b) + DF(a) ;
T ambii factori
influenteaza pozitiv variatia fenomenului economico-financiar
"F", influenta hotaritoare avind-o factorul "a".
2. IN
MARIMI RELATIVE (PROCENTUALE)
F
= 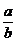 ;
; 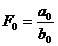 ;
; 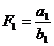
a)-
FACTORUL CANTITATIV SE AFLA LA NUMARATOR
Calculam DF % = 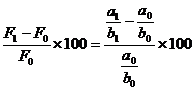 ;
;
Din care :
1) DF % (a) = 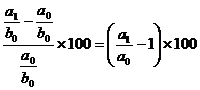 ,
,
DF % (b) = 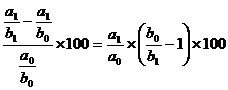 ;
;
Verificam corelatia :
DF % = DF % (a) + DF % (b)
EXEMPLU - Consideram datele
din tabelul de mai jos :
ETAPA 1 - Consideram ca F este dat de
raportul :
F = 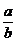 ;
; 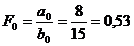 ;
; 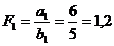
∆F% = 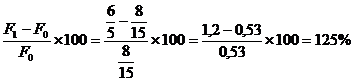 ,
,
Din care:
∆F% (a) = 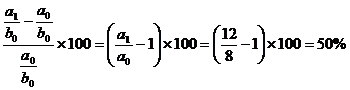 ,
,
∆F%(b) = 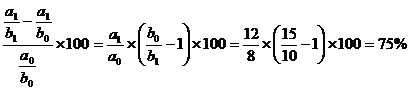 .
.
Verificam corelatia : DF% = DF%(a) + DF%(b) ;
b) -
FACTORUL CANTITATIV SE AFLA LA NUMITOR
F = 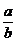 ;
; 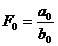 ;
; 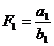
Calculam
DF % =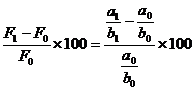
Din care :
DF % (b) =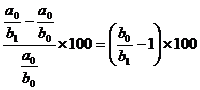 ,
,
DF % (a) =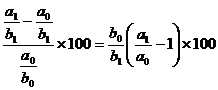 .
.
Verificam corelatia : DF % = DF % (b)
+ DF % (a)
EXEMPLU - Consideram datele
din tabelul de mai jos :
ETAPA 1 - Consideram ca F este dat de
raportul :
F = 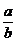 ;
; 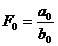 =
=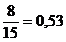 ;
; 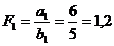
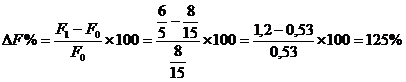 ,
,
Din care:
1) 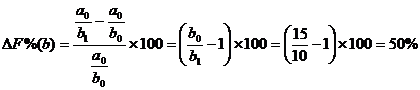 ,
,
2) 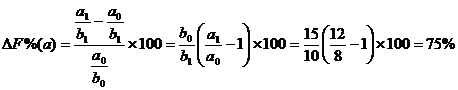 .
.
Verificam corelatia : DF% = DF%(a) + DF%(b) ,
3 - METODA
DETERMINARII ACTIUNII IZOLATE A FACTORILOR
=
se utilizeaza in cazul unui produs sau raport de factori;
= se foloseste doar
criteriul care afirma ca "substituirea factorilor are loc in mod
succesiv si nu simultan"
Consideram un produs de factori : F =
a x b x c x d
La timpul t0 , F0 = a0 b0 c0
d0
La timpul t1 , F1 = a1 b1 c1
d1
Variatia fenomenului este
data de relatia:
DF = F1 - F0
= a1 b1 c1 d1 - a1
b0 c0 d0 ,
Din care :
DF(a) = a1 b0
c0 d0 - a0 b0 c0 d0 = ( a1 - a0 ) b0 c0
d0;
DF(b) = a0 b1
c0 d0 - a0 b0 c0 d0 = a0 ( b1 - b0)
c0 d0;
DF(c) = a0 b0 c1
d0 - a0 b0 c0 d0 = a0 b0 ( c1
- c0 ) d0;
DF(d) = a0 b0
c0 d1 - a0 b0 c0 d0 = a0 b0 c0 (
d1 - d0).
Verificam corelatia : DF = DF(a) + DF(b) + DF(c) + DF(d) + R
R = marime reziduala ce reprezinta
:
a)-influenta altor factori
decit cei mentionati;
b)-influenta
interactiunii factorilor a, b, c, d.
EXEMPLU - Consideram datele
din tabelul de mai jos :
ETAPA 1 : Modelul
factorial este : F = a x b x c x d
DF = F1 - F0
= 13.200 - 9.600 = 3.600 u.m.
Din care :
DF(a) = (a1 - a0)
b0 c0 d0 = (12 - 8) x 15 x 20 x 4 = 4.800 u.m.
DF(b) = a0 (b1
- b0 ) c0 d0 = 8 (10 - 15) x 20 x 4 = - 3.200 u.m.
DF(c) = a0 b0
(c1 - c0) d0 = 8 x 15 (22 - 20) x 4 = 960 u.m.
DF(d) = a0 b0
c0 (d1 - d0) = 8 x 15 x 20 (5 - 4) = 2.400 u.m.
Verificam corelatia : DF = DF(a) + DF(b) + DF(c) + DF(d) + R
3.600 = 4.800 + (-3.200) + 960 + 2.400
+ R
3.600 = 4.960 + R R = - 1.360
4 - METODA
CORELATIEI
=
se utilizeaza in situatia in care fenomenul economico-financiar este
influentat de o serie de factori dupa modele economico-financiare de
tip stochastic (statistic-probabilistic)
=
relatiile de influenta sunt cu unul, doi sau mai multi
factori, folosind in acest sens :
1) - regresia liniara cu un
factor independent , y
= ax + b ,
Unde
x = factorul independent , y =
fenomenul economico-financiar analizat;
2) - regresia liniara cu doi
factori independenti, y = a1x1 + a2x2
Unde
x1, x2 = factori independenti, y = fenomenul economico-financiar analizat;
3) - regresia liniara cu "n"
factori independenti, 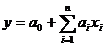 ;
;
4) - regresie parabolica cu
un singur factor independent, y = ax2 + bx + c ;
5) - regresie parabolica cu
doi factori independenti,
y = a0 + a1x1
+ a11x12 + a2x2 + a22x22
+ a12x1x2 ;
6) - regresie logartimica, 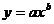 ;
;
7) - regresie
semilogaritmica, 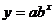 ;
;
8) - regresie hiperbolica,  .
.
a, b, c = parametrii de regresie
si se estimeaza (se determina) pe baza unor serii statistice,
folosind metoda "celor mai mici patrate" ( = se calculeaza parametrii
a, b, c, astfel incit, suma patratelor diferentelor dintre fenomenul
economico-financiar real si cel teoretic sa fie cit mai mica)
In descrierea dependentei
dintre factorii de influenta si fenomenul economico-financiar
analizat sunt folosite o serie de regresii, iar intensitatea legaturii
este data de raportul sau de coeficientul de corelatie,
calculati dupa relatiile :
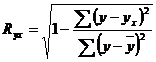 ,
,
Ryx = raport de
corelatie folosit in cazul regresiilor nelineare; valoarea lui este
cuprinsa intre 0 si 1
Cu cat valoarea este mai
apropiata de zero, cu atit demonstreaza o legatura mai
putin stransa dintre factor si fenomenul economico-financiar
analizat. Cu cat valoarea este mai apropiata de 1, cu atat demonstreaza
o legatura mai stransa dintre factor si fenomenul
economico-financiar analizat.
In
cazul relatiilor lineare, intensitatea legaturii dintre factori
si fenomenul analizat se determina cu ajutorul coeficientului de
corelatie, calculat cu relatia :
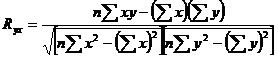 ,
,
Pentru valori apropiate de 1
si (-1) avem o legatura strinsa intre factori si
fenomen.
Pentru valori apropiate de zero
avem o legatura mai putin stransa intre factori si
fenomen.
Valoarea coeficientului de
corelatie cuprins intre 0 si (-1) semnifica existenta unei
corelatii inverse T marirea factorului independent "x" contribuie la
reducerea fenomenului economico-financiar sau atunci cand "x" scade, "y"
creste.
Atunci cand raportul de corelatie
este cuprins intre 0 si 1 avem o legatura directa Tfactorul "x" contribuie
la cresterea lui "y".
5 - METODA
SCORURILOR
Presupune folosirea unui model de regresie
lineara cu "n" factori independenti de forma :
 ,
,
a1..an
= coeficienti de regresie
x1..xn
= variabile independente (calculate sub forma ratelor)
STABILIREA SCORULUI = presupune parcurgerea
urmatoarelor etape :
1) - alegerea unui esantion
de firme care sa cuprinda doua categorii de intreprinderi:
a)
- falimentare sau aflate in dificultate;
b)
- fara probleme financiare.
2) - compararea
celor doua grupe de intreprinderi, pe un interval de timp suficient de
mare, folosind o serie de indicatori economico-financiari;
3) - selectarea indicatorilor
care realizeaza cea mai buna discriminare;
4) - elaborarea unui model linear
al indicatorilor reprezentativi (functia scor).
Scorul constatat la nivelul unei
firme permite estimarea riscului de faliment la un moment dat.
6 - METODA
RATELOR
RATA =
reprezinta un raport intre doi indicatori comparabili din punct de vedere
economic, cu o semnificatie superioara celor doi termeni luati
separat.
RATELE = se grupeaza
in trei categorii :
a) - rate de structura = reprezinta contributia
partilor la formarea fenomenului;
b) - rate de eficienta = reflecta corelatia dintre
efort si efect:
1) - efect-efort :
- rata rentabilitatii economice;
-
rata rentabilitatii financiare;
-
rata rentabilitatii resurselor consumate;
-
rata rentabilitatii capitalurilor.
2) - efort-efect:
- ratele de eficienta ale cheltuielilor;
- costul unitar.
c) - rate ale echilibrului financiar = reflecta corelatiile dintre
posturi sau grupe de posturi din bilantul contabil al intreprinderii
(elementele din activ si cele din pasiv ):
-rate de
lichiditate;
-rate de
solvabilitate.


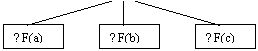



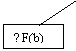
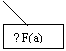
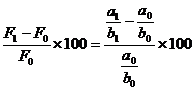 ;
;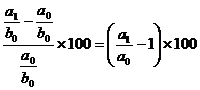 ,
,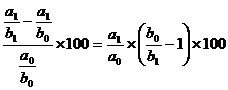
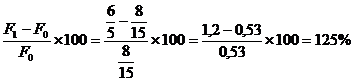 ,
,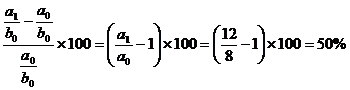 ,
, 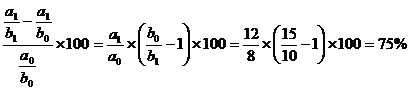 .
. 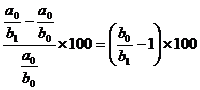 ,
,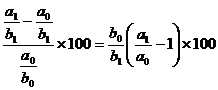 .
.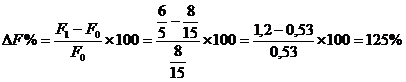 ,
,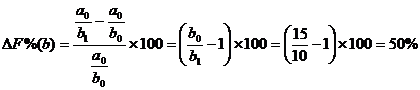 ,
,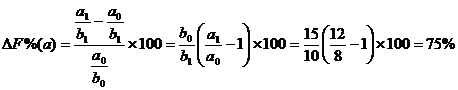 .
.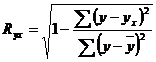 ,
,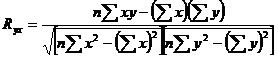 ,
,