Energia
oscilatorului intretinut
In continuare se
analizeaza energia oscilatorului intretinut, neamortizat si a
celui amortizat
Energia oscilatorului
intretinut si neamortizat
Daca oscilatorul
este neamortizat si intretinut de o forta perturbatoare
sinusoidala, ecuatia diferentiala a miscarii se
obtine din ecuatia (3.4.45) in care coeficientul de amortizare c = 0.
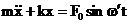 (3.4.75)
(3.4.75)
Solutia
ecuatiei diferentiale este:
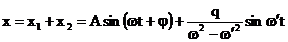 (3.4.76)
(3.4.76)
Atunci cand conditiile
initiale sunt:
la t = 0 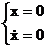 (3.4.77)
(3.4.77)
ecuatia miscarii oscilatorii este:
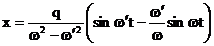 (3.4.78)
(3.4.78)
iar miscarea sistemului oscilant este nearmonica.
La rezonanta, 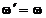 iar sistemul oscilant
va avea ecuatia de miscare:
iar sistemul oscilant
va avea ecuatia de miscare:
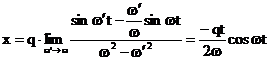 (3.4.79)
(3.4.79)
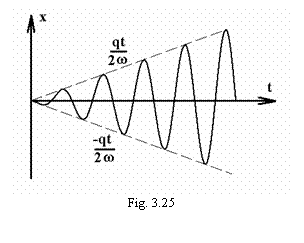 Graficul
miscarii oscilatorii neamortizate si intretinute de
forta perturbatoare sinusoidala, la rezonanta, este
prezentat in figura 3.25
Graficul
miscarii oscilatorii neamortizate si intretinute de
forta perturbatoare sinusoidala, la rezonanta, este
prezentat in figura 3.25
In cazul
oscilatiilor neamortizate si intretinute, pornind de la
ecuatia diferentiala a miscarii, prin inmultire
cu 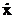 se obtine:
se obtine:
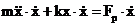 (3.4.80) sau:
(3.4.80) sau: 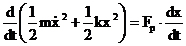 (3.4.81)
(3.4.81)
Tinand cont de
expresiile energiei cinetice si a energiei potentiale date de
relatia (3.4.43) se obtine: 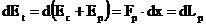 (3.4.82)
(3.4.82)
in care 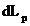 este lucrul mecanic
elementar efectuat de forta perturbatoare asupra sistemului. Deci,
sistemul oscilant isi creste energia datorita lucrului mecanic
al fortei perturbatoare.
este lucrul mecanic
elementar efectuat de forta perturbatoare asupra sistemului. Deci,
sistemul oscilant isi creste energia datorita lucrului mecanic
al fortei perturbatoare.
In cazul rezonantei,
pornind de la ecuatia de miscare a oscilatorului, descrisa de
relatia (3.4.79) se poate calcula lucrul mecanic efectuat de forta
perturbatoare asupra sistemului in timp de o perioada. Diferentiand
relatia (3.4.79) se obtine:
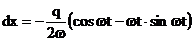 (3.4.83)
(3.4.83)
Lucrul mecanic al
fortei perturbatoare, la rezonanta, intr-o perioada, este:
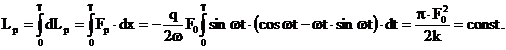 (3.4.84)
(3.4.84)
Deci, in cazul oscilatiilor intretinute, neamortizate, in
timp de o perioada, la rezonanta, sistemul primeste din
partea fortei perturbatoare o cantitate de energie constanta. De
aceea, energia sistemului creste, iar amplitudinea oscilatiei
creste liniar, asa cum se vede in figura 3.25.
Energia oscilatorului
intretinut si amortizat
In cazul oscilatiilor
intretinute si amortizate, se obtine, pe baza aceluias
rationament descris anterior, relatia: 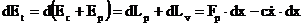 (3.4.85)
(3.4.85)
in care 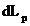 este lucrul mecanic
elementar efectuat de forta perturbatoare, iar
este lucrul mecanic
elementar efectuat de forta perturbatoare, iar 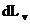 este lucrul mecanic
elementar efectuat de forta de frecare vascoasa asupra sistemului. Se
observa ca lucrul mecanic elementar efectuat de forta
perturbatoare este pozitiv si duce la cresterea energiei totale
a sistemului, iar lucrul mecanic
elementar efectuat de forta de frecare vascoasa este negativ si
duce la scaderea energiei totale a sistemului.
este lucrul mecanic
elementar efectuat de forta de frecare vascoasa asupra sistemului. Se
observa ca lucrul mecanic elementar efectuat de forta
perturbatoare este pozitiv si duce la cresterea energiei totale
a sistemului, iar lucrul mecanic
elementar efectuat de forta de frecare vascoasa este negativ si
duce la scaderea energiei totale a sistemului.
Pornind de la
ecuatia de miscare a sistemului in regim permanent (3.4.59), prin
derivare si diferentiere se obtine:
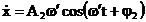 (3.4.86)
(3.4.86)
si: 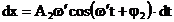 (3.4.87)
(3.4.87)
Lucrurile mecanice
elementare 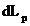 si
si 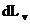 vor avea expresiile:
vor avea expresiile:
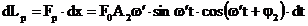 (3.4.88)
(3.4.88)
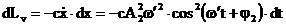 (3.4.89)
(3.4.89)
Integrand cele doua
expresii, pe intervalul de timp de o perioada, se obtine:
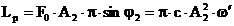 (3.4.90)
(3.4.90)
si: 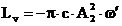 (3.4.91)
(3.4.91)
Deci, in timp de o
perioada, in regim permanent 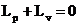 (3.4.92)
(3.4.92)
iar: 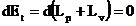 sau:
sau: 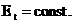 (3.4.93)
(3.4.93)
Energia totala a
oscilatorului este constanta, deoarece energia primita de sistem de
la forta perturbatoare este cedata in acelasi timp si in
aceeasi cantitate, sub forma de lucru mecanic de frecare.


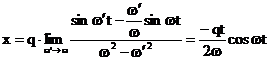 (3.4.79)
(3.4.79) Graficul
miscarii oscilatorii neamortizate si intretinute de
forta perturbatoare sinusoidala, la rezonanta, este
prezentat in figura 3.25
Graficul
miscarii oscilatorii neamortizate si intretinute de
forta perturbatoare sinusoidala, la rezonanta, este
prezentat in figura 3.25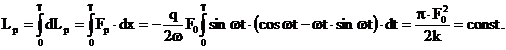 (3.4.84)
(3.4.84)