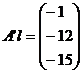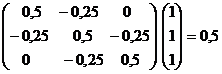Marimi masurate indirect de aceeasi
precizie
1 Calculul valorilor probabile
Caracteristica acestei categorii de
masuratori este forma sistemului ecuatiilor de erori. Este un sistem cu 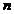 ecuatii si
ecuatii si  necunoscute(
necunoscute( -necunoscute
principale) - termenii liberi fiind marimi masurate direct cu aceeasi
precizie.
-necunoscute
principale) - termenii liberi fiind marimi masurate direct cu aceeasi
precizie.
Astfel:
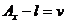 (
(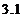 )
)
in care: 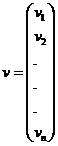

 ;
; 
Sistemul algebric nedeterminat este posibil de rezolvat, in conditia:
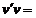 minim (
minim (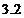 )
)
Obtinandu-se valorile probabile ale necunoscutelor principale din
sistemul:


respectiv:

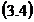
2 Calculul coeficientilor de pondere
Matricea
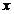 data
de relatia
data
de relatia 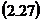 este
o functie directa de matricea
este
o functie directa de matricea  , ale
carei elemente sunt marimi masurate si de aceesi
precizie. In consecinta se poate aplica relatia
, ale
carei elemente sunt marimi masurate si de aceesi
precizie. In consecinta se poate aplica relatia 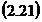 si rezulta:
si rezulta:
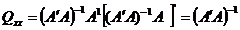
Respectiv:
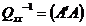
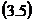
 - matricea coeficientilor de pondere
corespunzatori marimilor masurate direct.
- matricea coeficientilor de pondere
corespunzatori marimilor masurate direct.
Pentru determinarea
coeficientului al unei functii se obtine scriind:
 ;
; 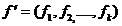
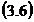
in care:
 sunt
marimi obtinute cu ecuatia
sunt
marimi obtinute cu ecuatia
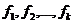 coeficienti ai necunsocutelor,
constanti ca si
coeficienti ai necunsocutelor,
constanti ca si 
Conform cu cele
stabilite:


Iar:
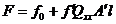
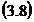
si ca urmare:

Pentru calculul erorilor
medii patratice ale marimilor obtinute indirect si ale unei
functii de aceste marimi, este necesar a se calcula eroarea medie
patratica a unei singure masuratori cu relatia:

 numarul de marimi
masurate direct
numarul de marimi
masurate direct 
 numarul marimilor
obtinute indirect
numarul marimilor
obtinute indirect
In acest fel:
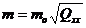 si
si 
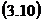
Dar 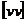 se obtine astfel:
se obtine astfel:

si 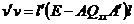
 matricea unitatea
matricea unitatea 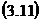
Exemplu:
Consideram
in punctul geodezic  directiile
directiile
 .
.
Intre aceste directii se masoara unghiurile  dupa metoda
seriilor binare (fig 4.)
dupa metoda
seriilor binare (fig 4.)
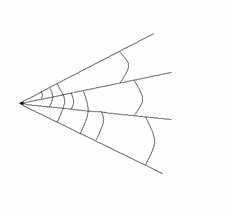 Se obtin din masuratori,
valorile:
Se obtin din masuratori,
valorile:

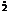
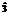
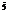



Fig. 4
Cum insa:

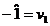
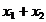
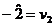
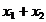


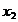
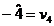
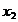

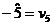

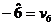
Si in conditiile
in care:
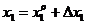 ,
, 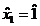
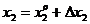 ,
, 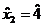
 ,
, 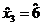
Se obtine:




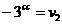

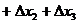
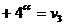
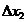



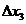
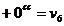
Vom scrie, pentru determinarea
valorilor probabile, egalitatea:
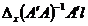
 ;
;  ;
; 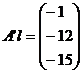
Se
obtine:
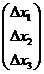

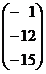 ;
; 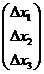 =
=
Coeficientii
de pondere ai marimilor obtinute indirect respectiv ai marimilor
stabilite cu corectiiele probabile sunt dati de elementele care
formeaza diagonala matricei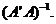
Astfel:

Se stabileste in continuare:

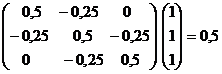
Cum insa:

Erorile
medii patratice ale marimilor obtinute indirect si a
functiei pot fi simplu obtinute cu relatiile 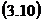 .
.


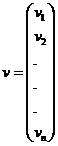




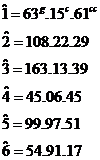
 ;
;  ;
;