Oscilatorul armonic liniar
Urmarim miscarea
unui punct material M pe un cerc de raza R. Proiectia acestuia pe
unul din diametrele cercului (in figura cel vertical) efectueaza o
miscare oscilatorie.
|

Figura 1
Obs: Se considera axa verticala ca
fiind Oy
si cea orizontala Ox.
|
Se poate demonstra ca legea de miscare a punctului P este:
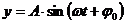 (1.1) (1.1)
unde: y
reprezinta elongatia: distanta de la pozitia de echilibru
pana la pozitia oscilatorului la momentul respectiv. Fiind o
distanta, se masoara in metri;
A: amplitudinea,
reprezinta elongatia maxima (distanta maxima la care
se departeaza oscilatorul fata de pozitia de
echilibru). Se masoara in metri;
: pulsatia oscilatorului. Se
masoara in rad/sec (radiani pe secunda);
t
este timpul;
 este faza
initiala adica unghiul facut de raza R cu axa Ox
la momentul initial. este faza
initiala adica unghiul facut de raza R cu axa Ox
la momentul initial.  atunci cand punctul
nu isi incepe miscarea pornind din pozitia de echilibru. Faza
se masoara in radiani. atunci cand punctul
nu isi incepe miscarea pornind din pozitia de echilibru. Faza
se masoara in radiani.
|
Valorile unghiurilor in
radiani precum si valorile sinusurilor si cosinusurilor sunt date in Anexa
nr. 1.
Deoarece
legea miscarii este o functie sinusoidala in raport cu
timpul, miscarea este oscilatorie armonica.
Intre pulsatie,
frecventa si perioada exista urmatoarele
relatii (care se pot demonstra):
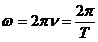 ;
;  ;
;  (1.2)
(1.2)
Cunoscand
legea de miscare se poate deduce expresia vitezei oscilatorului
armonic liniar:
 (1.3)
(1.3)
Obs.: Viteza depinde
cosinusoidal de timp. Valoarea ei este maxima atunci cand cosinusul este
maxim, adica 1. Deci: 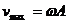 (1.4)
(1.4)
Deoarece
viteza variaza in timp, miscarea va fi accelerata si se poate deduce formula acceleratiei:
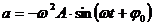 (1.5)
(1.5)
Obs.: La probleme, formula
acceleratiei se va lua in modul. Valoarea acceleratiei este maxima
atunci cand sinusul este maxim, adica 1. Deci: 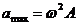 (1.6)
(1.6)
Acceleratia este produsa
de o forta, iar conform principiului II al mecanicii: F=m·a,
unde m este masa corpului (a punctului material care oscileaza). Deci,
asupra oscilatorului actioneaza forta:
 (1.7)
(1.7)
unde k este constanta oscilatorului. Din
relatia de mai sus observam ca:
 si
si 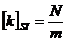 (1.8)
(1.8)
Utilizand
relatia (1.8) si formula pulsatiei din (1.2) se ajunge la
formulele perioadei si frecventei oscilatorului armonic liniar in
functie de masa si constanta oscilatorului:
 si
si 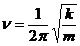 (1.9)
(1.9)
Formula fortei se
scrie vectorial:  . Aceasta forta este de tip elastic. Valoarea
maxima a fortei este:
. Aceasta forta este de tip elastic. Valoarea
maxima a fortei este:  (1.10)
(1.10)
Un
punct material in miscare sub actiunea unei forte de tip elastic
se numeste oscilator armonic liniar.
Oscilatorul armonic liniar este un
punct material in miscare, deci el va avea energie cinetica:
 (1.11)
(1.11)
Deoarece oscilatorul se
misca sub actiunea unei forte elastice, el va avea energie
potentiala elastica:
 (1.12)
(1.12)
Suma dintre energiile cinetica
si potentiala reprezinta energia totala a
oscilatorului:
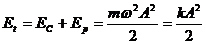 (1.13)
(1.13)
Obs.: Energiile cinetica
si potentiala variaza in timp astfel incat suma lor (
energia totala ) este constanta. Exista o transformare
continua a energiei cinetice in energie potentiala si
invers. Cand corpul are energie cinetica maxima ( in pozitia de
echilibru ), energia potentiala este minima ( adica 0 ). In
pozitiile extreme ( pentru y=A ) energia potentiala este
maxima, iar energia cinetica este nula.


