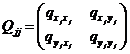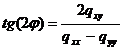Prelucrarea
Masuratorilor Prin Metoda Observatiilor Indirecte (Modelul
Gauss-Markov)
1.1. Cazul General
In cazul masuratorilor
indirecte,valoarea marimilor care ne intereseaza se obtine prin
intermediul unei (unor) marimi masurate direct, marimile
masurate direct si cele de determinat fiind functional
dependente intre ele.
Fie  valorile medii ale
unor marimi, rezultante din masuratori directe si
valorile medii ale
unor marimi, rezultante din masuratori directe si  , marimile ce urmeaza a fi determinate indirect.
, marimile ce urmeaza a fi determinate indirect.
Sa presupunem ca intre
marimile fizice masurate direct si parametrii  de determinat,
exista urmatoarele dependente functionale:
de determinat,
exista urmatoarele dependente functionale:
 , unde: i = 1..n (1.1)
, unde: i = 1..n (1.1)
Relatia (1.1) defineste modelul functional.
Problema care se pune este, ca din sistemul
(1.1) sa deducem cele mai probabile (cele mai bune) valori pentru  .
.
Daca valorile masurate direct 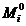 ar fi neafectate de
erori, atunci sistemul (1.1) se poate scrie sub forma:
ar fi neafectate de
erori, atunci sistemul (1.1) se poate scrie sub forma:
 , i = 1..n (1.2)
, i = 1..n (1.2)
unde: cu n s-a notat numarul de
masuratori efectuate, iar cu h numarul de necunoscute.
Se fac urmatoarele observatii:
- daca n < h atunci, din punct de
vedere matematic, sistemul este nedeterminat; din punct de vedere 'geodezic',
numarul de masuratori este insuficient pentru rezolvarea problemei.
- daca n = h atunci, din punct de vedere
matematic sistemul este compatibil cu solutie unica; din punct de vedere
'geodezic', se masoara numai strictul necesar pentru rezolvarea problemei.
- daca n > h atunci, din punct de
vedere matematic sistemul este incompatibil; din punct de vedere 'geodezic',
datorita erorilor de masurare, sistemul devine incompatibil.
In practica, cu oricata grija
si pricepere si in oricat de bune conditii s-ar efectua
masuratorile, acestea sunt afectate in mod inerent de erori.
Datorita erorilor de masurare,
sistemul (1.1) este incompatibil, de aceea marimilor masurate trebuie
sa li se aplice niste corectii  , astfel incat sistemul sa fie compatibil cu
necunoscutele
, astfel incat sistemul sa fie compatibil cu
necunoscutele  .
.
Astfel sistemul (1.1) devine:
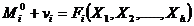 , unde i = 1..n, n>h (1.3)
, unde i = 1..n, n>h (1.3)
Sistemul (1.3) este compatibil dar
nedeterminat deoarece avem n ecuatii (n marimi cunoscute) si n + h
necunoscute (n corectii aplicate marimilor masurate si h
corectii X aplicate parametrilor determinati indirect).
Valorile cele mai probabile ale
corectiilor se determina aplicand metoda celor mai mici patrate.
Deci marimile v, reprezinta
corectiile ce trebuiesc aplicate marimilor masurate direct,
pentru a fi satisfacute toate ecuatiile de tipul (1.1) ce pot fi
intocmite, pentru rezolvarea unei anumite probleme.
1.2. Liniarizarea ecuatiilor
Deoarece in majoritatea cazurilor
functiile 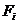 din relatia (1.1)
sunt neliniare, compensarea devine foarte greoaie. De aceea, pentru
usurarea calculelor de compensare, aceste ecuatii se aproximeaza
cu niste ecuatii liniare ce se obtin prin dezvoltarea in serie Taylor, in
vecinatatea unor valori
din relatia (1.1)
sunt neliniare, compensarea devine foarte greoaie. De aceea, pentru
usurarea calculelor de compensare, aceste ecuatii se aproximeaza
cu niste ecuatii liniare ce se obtin prin dezvoltarea in serie Taylor, in
vecinatatea unor valori  , apropiate de cele adevarate.
, apropiate de cele adevarate.
Valorile probabile ale necunoscutelor vor fi
deci:
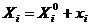 (1.4)
(1.4)
in care xi,, reprezinta
niste corectii ce urmeaza sa le determinam prin
compensare.
Aceste corectii trebuie sa fie
suficient de mici, astfel ca in dezvoltarea in serie sa putem neglija
termenii de ordinul 2 si mai mari.
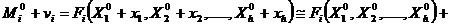
 (1.5)
(1.5)
Notatii:
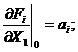

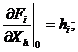 (1.6)
(1.6)
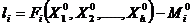 (1.7)
(1.7)
Regula practica de calcul a termenului
liber este:
Termenul liber =
Valoarea calculata - Valoarea masurata (1.8)
Relatiile (1.5) vor deveni cu ajutorul
notatiilor (1.6) si (1.7):
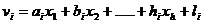 (1.9)
(1.9)
Aceasta relatie poarta numele
de: 'sistemul liniar al ecuatiilor
de corectii'.
Modelul
stochastic:
Vectorul marimilor masurate, fiind
un vector n dimensional si tinand seama si de relatia :
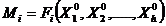 (1.10)
(1.10)
rezulta ca matricea de
varianta - covarianta va avea forma:
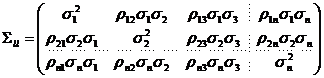 (1.11)
(1.11)
In relatia (1.11) s-au folosit
notatiile:
 - care este
varianta masuratorii
- care este
varianta masuratorii 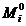
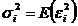 (1.12)
(1.12)
 - care este
coeficientul de corelatie intre marimile
- care este
coeficientul de corelatie intre marimile 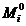 si
si 
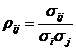 si
si 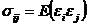 (1.13)
(1.13)
unde 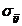 este covarianta
masuratorilor
este covarianta
masuratorilor 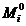 si
si 
Trebuie mentionat ca in
relatiile (1.12) si (1.13) termenul 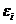 este definit uzual ca
eroare adevarata. Erorile adevarate sunt definite ca
diferente intre masuratorile
este definit uzual ca
eroare adevarata. Erorile adevarate sunt definite ca
diferente intre masuratorile  si valorile lor
adevarate
si valorile lor
adevarate  si se
calculeaza cu urmatoarea formula:
si se
calculeaza cu urmatoarea formula:
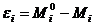 (1.14)
(1.14)
In cazul masuratorilor independente
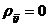 pentru
pentru  si
si  , matricea de varianta - covarianta
devine diagonala si anume:
, matricea de varianta - covarianta
devine diagonala si anume:
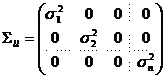 (1.15)
(1.15)
Relatia (1.15) mai poate fi scrisa
si sub urmatoarea forma:
 (1.16)
(1.16)
Tinand cont ca: 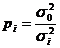 , rezulta ca:
, rezulta ca:
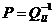 (1.17)
(1.17)
Daca masuratorile sunt
independente si de aceiasi precizie relatia (1.16) devine:
 (1.18)
(1.18)
unde:
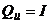 (1.19)
(1.19)
Se fac urmatoarele observatii:
- fiecare masuratoare
genereaza cate o ecuatie de corectie;
- din expresiile coeficientilor si
termenilor liberi, se observa ca marimea masurata
direct 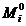 , deci cea care este afectata de erori, intervine numai
in termenul liber;
, deci cea care este afectata de erori, intervine numai
in termenul liber;
- din relatia (1.7) se deduce ca
eroarea termenului liber este egala cu eroarea marimii masurate,
deoarece marimile  sunt niste
constante. Rezulta deci ca eroarea unei ecuatii de corectie
este egala cu eroarea termenului liber a acesteia, coeficientii
sunt niste
constante. Rezulta deci ca eroarea unei ecuatii de corectie
este egala cu eroarea termenului liber a acesteia, coeficientii  putand fi
considerati niste constante lipsite de erori.
putand fi
considerati niste constante lipsite de erori.
- daca marimile masurate 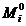 , sunt determinate cu aceiasi precizie si
ecuatiile sistemului liniar al corectiilor vor avea aceiasi
precizie. In caz contrar vom avea un sistem liniar al ecuatiilor de
corectii ponderat.
, sunt determinate cu aceiasi precizie si
ecuatiile sistemului liniar al corectiilor vor avea aceiasi
precizie. In caz contrar vom avea un sistem liniar al ecuatiilor de
corectii ponderat.
1.3. Rezolvarea sistemelor de ecuatii liniare
Metodele de rezolvare a sistemelor de
ecuatii liniare se impart in doua grupe:
1. Metode exacte, care dau un algoritm finit
pentru calculul solutiei (de exemplu regula lui Cramer sau metoda
eliminarii lui Gauss);
2. Metode iterative, care permit sa
gasim solutia cu o eroare arbitrara mica (dar nenula),
sub forma unui sir convergent de vectori Rn (unde n
reprezinta numarul ecuatiilor si al necunoscutelor din
sistemul dat), a carui constructie se face printr-un proces unic,
numit 'proces de iteratie'.
Desigur, metodele exacte nu dau solutia
numerica decat cu aproximatie, in masura in care rezultatul unui
calcul simplu, de exemplu rezultatul impartirii unor numere prime
intre ele, nu se poate da decat cu aproximatie oricat de mica, dar
nenula.
Metodele iterative sunt, de regula,
simple si comode pentru folosirea masinilor de calcul. Dar fiecare
proces iterativ are un domeniu limitat de aplicare, deoarece un proces iterativ
poate fi divergent pentru un sistem dat, sau poate sa convearga atat
de incet incat sa fie practic inutilizabil.
De regula, metodele iterative se
aplica atunci cand coeficientii diagonali ai sistemului sunt mai mari
in valoare absoluta decat coeficientii nediagonali, convergenta
fiind asigurata in acest caz. Sistemele normale, rezultate in procesul de
compensare, se bucura in general de aceasta caracteristica (mai
ales in cazul retelelor de nivelment).
Rezolvarea sistemelor de ecuatii normale
cu un numar mare de necunoscute necesita calcule destul de
laborioase, iar erorile de calcul pot atinge valori apreciabile.
De aceea, caracteristicile si structura
ecuatiilor normale, impun alegerea cu discernamant a celor mai adecvate
metode de rezolvare.
1.4. Verificarile principale la compensarea prin metoda
masuratorilor
indirecte
4.1. Liniarizarea ecuatiilor si
stabilirea valorilor aproximative pentru necunoscute
Controlul
acestei etape se face prin verificarea principala a compensarii care consta
in determinarea in dublu mod a valorilor marimilor compensate mi, si anume:
Prin introducerea
necunoscutelor: X = X0 + xi, in ecuatiile initiale, trebuind sa avem:
 (1.20)
(1.20)
Daca conditia
din relatia (1.20) de mai sus nu este indeplinita, inseamna
ca liniarizarea, dupa regula
Taylor, nu a fost bine executata, sau valorile aproximative au fost alese nefavorabil, astfel ca termenii de
ordinul II si
superiori neglijati au valori ce influenteaza
compensarea,
in acest caz intreaga
compensare trebuie refacuta, rezultatele obtinute X, fiind folosite ca noi valori aproximative.
1.4.2 Intocmirea
ecuatiilor normale
Verificarea
se face cu ajutorul sumelor pe randuri.
1.4.3 Rezolvarea
ecuatiilor normale
Verificarea
se face cu ajutorul sumelor pe randuri din schema Gauss ( in faza
de reducere) si prin introducerea necunoscutelor in sistemul normal.
1.4.4 Calculul
corectiilor
Verificarea
se face prin calculul [ vv ], prin mai multe metode.
1.5. Tratarea matriceala a masuratorilor indirecte.
Cazul masuratorilor ponderate.
Fie sistemul liniar al ecuatiilor de
corectii ponderat (de pondere pi):
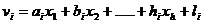 , i = 1..n, n>h (1.21)
, i = 1..n, n>h (1.21)
Notatii:
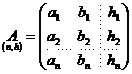 ; matricea coeficientilor sistemului de ecuatii de
corectii,
; matricea coeficientilor sistemului de ecuatii de
corectii,
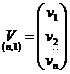 ; vectorul corectiilor sistemului de ecuatii de
corectii,
; vectorul corectiilor sistemului de ecuatii de
corectii,
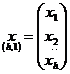 ; vectorul corectiilor aduse parametrilor
determinati indirect,
; vectorul corectiilor aduse parametrilor
determinati indirect,
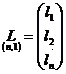 ; vectorul termenilor liberi,
; vectorul termenilor liberi,
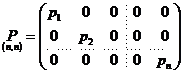 ; matricea ponderilor sistemului de ecuatii de
corectii. (1.22)
; matricea ponderilor sistemului de ecuatii de
corectii. (1.22)
Cu ajutorul notatiilor (1.22), din
relatia (1.21) rezulta ca forma generala a sistemului de
ecuatii de corectii va fi:
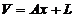 (1.23)
(1.23)
Sistemul (1.22) este nedeterminat. Valorile
cele mai probabile se determina utilizand metoda celor mai mici
patrate, aceasta putandu-se exprima sub forma:
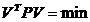 (1.24)
(1.24)
efectuand inlocuirile, folosindu-ne de
relatiile (1.23) si (1.24) rezulta:
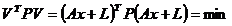 (1.25)
(1.25)

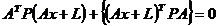

 (1.26)
(1.26)
Relatia (1.26) reprezinta sistemul
normal in cazul masuratorilor indirecte ponderate.
Rezolvarea sistemului normal
se face astfel:
Notam  si (1.26) devine:
si (1.26) devine:
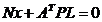
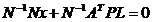
 (1.27)
(1.27)
Relatia (1.27) reprezinta
rezolvarea sistemului normal in cazul masuratorilor indirecte
ponderate.
Corectiile se vor aplica marimilor
determinate indirect, marimilor aproximative rezultand marimile
estimate:
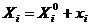 (1.28)
(1.28)
unde:
 - reprezinta valori compensate
- reprezinta valori compensate
 - reprezinta valori aproximative (provizorii)
- reprezinta valori aproximative (provizorii)
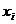 - reprezinta corectiile aplicate valorilor
aproximative.
- reprezinta corectiile aplicate valorilor
aproximative.
Cu ajutorul valorilor determinate in
relatia (1.28) se determina vectorul rezidurilor 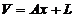 , care se aplica
marimilor masurate
, care se aplica
marimilor masurate 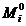 , rezultand marimile estimate ale acestora
, rezultand marimile estimate ale acestora 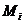 date de relatia:
date de relatia:
 (1.29)
(1.29)
1.6. Calculul preciziilor in cazul masuratorilor indirecte
ponderate
Pentru evaluarea preciziilor se folosesc
urmatoarele relatii:
1. Eroarea medie patratica a
unitatii de pondere
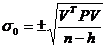 ; (1.30)
; (1.30)
unde:
n -
reprezinta numarul de ecuatii (numarul de masuratori);
h -
reprezinta numarul de necunoscute.
2. Erorile medii patratice ale
necunoscutelor
 ; (1.31)
; (1.31)
unde cu Q s-a notat matricea cofactorilor
 (1.32)
(1.32)
3. Eroarea medie patratica a unei
functii de marimi determinate indirect
Fie functia  , unde parametrii
, unde parametrii  reprezinta
marimi determinate indirect. Eroarea medie patratica a acestei
functii este:
reprezinta
marimi determinate indirect. Eroarea medie patratica a acestei
functii este:
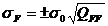 , (1.33)
, (1.33)
unde:
 (1.34)
(1.34)
iar
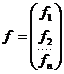 cu
cu 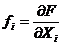 ; (1.35)
; (1.35)
1.7. Tratarea matriceala a masuratorilor indirecte. Cazul
masuratorilor de aceiasi precizie.
In acest caz forma generala a sistemului
de ecuatii de corectii va fi:
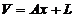 (1.36)
(1.36)
sistemul normal de ecuatii va avea
forma:
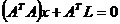 (1.37)
(1.37)
notam,
 (1.38)
(1.38)
-
reprezinta matricea normala a sistemului
cu notatia de mai sus si cu
ajutorul relatiei (1.37) rezulta:
 - vectorul
necunoscutelor (1.39)
- vectorul
necunoscutelor (1.39)
Relatia (1.38) reprezinta
rezolvarea sistemului normal in cazul masuratorilor indirecte de
aceiasi precizie.
Ca si in cazul masuratorilor
indirecte ponderate, corectiile obtinute din relatia (1.38) se
vor aplica marimilor aproximative rezultand marimile estimate. Cu
aceste marimi estimate se va determina vectorul rezidurilor, care se va
aplica marimilor masurate pentru a determina marimile estimate
ale acestora. Relatiile folosite in acest caz sunt similare celor folosite
in cazul masuratorilor indirecte ponderate.
1.8. Calculul preciziilor in cazul masuratorilor indirecte de
aceiasi precizie
Evaluarea preciziilor se va face cu
relatiile:
1. Eroarea medie patratica a unei
singure masuratori
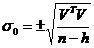 ; (1.40)
; (1.40)
unde:
n - reprezinta numarul de
ecuatii(numarul de masuratori);
h - reprezinta numarul de necunoscute.
2. Erorile medii patratice ale
necunoscutelor
 ; (1.41)
; (1.41)
unde cu Q s-a notat matricea cofactorilor
 (1.42)
(1.42)
1.9. Elipsa erorilor
In lucrarea de fata voi prezenta
consideratii privind doar elipsa
absoluta.
1.9.1.
Generalitati
Abaterea standard a parametrilor este
data de relatia (1.41) sau (1.31):
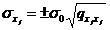 (1.43)
(1.43)
cu observatia ca  - reprezinta elementele de pe diagonala principala
a matricei cofactorilor:
- reprezinta elementele de pe diagonala principala
a matricei cofactorilor:
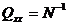 (1.44)
(1.44)
1.9.2.Elipsa
absoluta
Pozitia planimetrica a punctului
(determinat in urma compensarii prin metoda celor mai mici patrate),
depinde de doi parametri: x si y. Deoarece erorile medii patratice 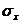 si
si  , isi modifica valorile la o schimbare de reper (o
rotatie a axelor) ceea ce produce o uniformitate in estimarea preciziei,
este necesar a se gasi un invariant care sa depinda numai de
precizia de masurare a elementelor retelei si de
configuratia acesteia. Acest invariant este elipsa erorilor(fig . ..).
, isi modifica valorile la o schimbare de reper (o
rotatie a axelor) ceea ce produce o uniformitate in estimarea preciziei,
este necesar a se gasi un invariant care sa depinda numai de
precizia de masurare a elementelor retelei si de
configuratia acesteia. Acest invariant este elipsa erorilor(fig . ..).
Fie un punct Pj de coordonate (Xj,Yj),
ale carui coordonate au fost obtinute in urma compensarii.
Totodata s-a obtinut si blocul bidimensional:
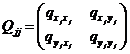 (1.45)
(1.45)
bloc extras din matricea generala a
cofactorilor : 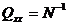 .
.
Elementele elipsei erorilor vor fi :
- semiaxele elipsei:
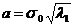 - semiaxa mare
- semiaxa mare
(1.46)
 - semiaxa mica
- semiaxa mica
- unghiul de orientare:
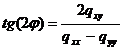 (1.47)
(1.47)
unde:
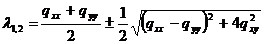 (1.48)
(1.48)
Elipsa erorilor poate fi utilizata
pentru:
- determinarea domeniului de incredere pentru
pozitia planimetrica a coordonatelor punctului
- determinarea directiilor dupa
care eroarea are valori extreme (maxim si minim)
- determinarea erorii pe orice directie
(determinata analitic sau grafic)
- optimizarea
retelei geodezice - masuratori sau a configuratiei
pentru obtinerea unor elipse omogene sau izotrope (fig 5 . . .).


 (1.5)
(1.5)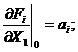

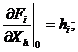 (1.6)
(1.6)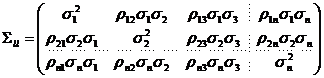
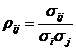 si
si 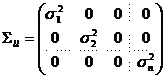


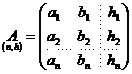 ; matricea coeficientilor sistemului de ecuatii de
corectii,
; matricea coeficientilor sistemului de ecuatii de
corectii,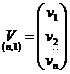 ; vectorul corectiilor sistemului de ecuatii de
corectii,
; vectorul corectiilor sistemului de ecuatii de
corectii,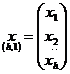 ; vectorul corectiilor aduse parametrilor
determinati indirect,
; vectorul corectiilor aduse parametrilor
determinati indirect,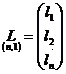 ; vectorul termenilor liberi,
; vectorul termenilor liberi,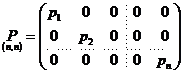 ; matricea ponderilor sistemului de ecuatii de
corectii.
; matricea ponderilor sistemului de ecuatii de
corectii.
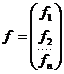 cu
cu