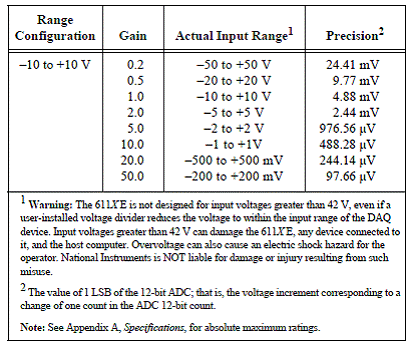Introducere
Conform
titlului, in prezenta lucrare se doreste implementarea in Matlab a unui sistem
de achizitie de date folosind placa de achizitie NI-PCI 6110.
O importanta deosebita
este acordata in zilele noastre utilizarii calculatorului in
prelucrarea numerica a datelor disponibile in urma
masurarii unor parametrii
fizici ai diferitelor procese industriale si nu numai. Calculatorul poate
fi privit acum ca un sistem de prelucrare numerica constituit pe baza
circuitelor integrate.
In majoritatea aplicatiilor de
acest tip se pune problema de a obtine informatii despre aceste
procese fizice in vederea memorarii si redarii pentru
comunicatie sau pentru control. Un astfel de proces este caracterizat prin
marimi fizice care ulterior pot fi transformate in semnale electrice
analogice utilizand traductoare. Pelucrarea acestor semnale se poate face
utilizand tehnici analogice sau numerice. In vederea unei prelucrari
numerice este necesara transformarea semnalelor analogice in semnale
numerice cu un sistem de achizitie date.
Semnalele electrice provenite de la
iesirile traductoarelor sunt supuse initial unor prelucrari
analogice primare si transformate in tensiuni electrice. Aceste
transformari sunt realizate la nivelul blocurilor circuitelor de
conditionare a semnalelor prin executia unor functii analogice
cum ar fi: amplificare, atenuare, filtrare, izolare, conversie tensiune curent,
etc. Semnalele numerice se obtin prin prelevarea la un moment dat a
valorilor semnalelor analogice si conversia acestor esantioane in
secvente numerice.
Componentele principale ale unui sistem de
achizitie (SAD) care executa aceste functii sunt circuitele de
esantionare si memorare si circuitele de conversie analog
numerica. Functiile principale executate de sistemul de prelucrare
numerica pot fi de filtrare numerica, identificare, reprezentare in
domeniul frecventa, analize "wavelet", clasificare, sortare,
identificare etc. In urma acestor operatii numerice de prelucrare se
obtin semnale numerice prelucrate care contin informatii despre
procesul fizic.
Achizitia de date are o
larga utilizare, in prezent fiind folosita in cele mai variate
domenii. Orice marime electrica, avand o forma analogica
trebuie transformata in prealabil,
intr-o
forma numerica pentru a putea fi prelucrata sub o forma sau
alta de un sistem de prelucrare. Monitorizarea unei temperaturi sau a
umiditatii dintr-un anumit mediu, monitorizarea semnalelor provenite
dintr-un mediu indistrial (in diverse aplicatii) sunt doar cateva exemple din
domeniile de aplicatii ce folosesc achizitia de semnal analogic.
Elementele hardware si software necesare:
Hardware
:
Placa
de achizitie PCI 6110 de la National Instruments
care dispune de:
Patru intrari analogice
simultane, cu 5 MS/s pentru fiecare canal;
Intrarea poate sa varieze
in intervalul ±42 V;
Doua iesiri analogice pe 16 biti, cu un canal de 4 MS/s si un canal dual de 2,5 MS/s ;
Opt linii intrare/iesire digitale; doua numaratoare pe 24
de biti;
Software de driver NI-DAQmx ce permite ca achizitia de semnal
sa fie comandata cu Matlab

Figura
1.1. Placa de achizitie NI-PCI 6110
Adaptorul
BNC-2110 care permite conectarea directa intre PC si
placa de achizitie.
Acesta incluce:
15 conectori BNC si un bloc
terminal cu 30 de pini
Are
un conector intrare/iesire pe 68 de pini ce conecteaza placile de achizitie
din seria E (PCI-6110E
Este
perfect pentru a simplifica conexiunile intre aparatura de masurare si
placa de achizitie .
Un
PC performant care sa suporte partea software.
Software
Mediul
de programare si simulare Matlab ce ne permite:
Crearea
aplicatiei de achizitie de semnal;
Depanare
si testare;
Simulare;
Pachetul
software NI-DAQmx ce permite ca
achizitia de semnal sa fie controlata din Matlab;
Software-ul
este disponibil fara costuri suplimentare in toate pachetale hardware
de achizitie de semnal de la National instruments. Acest driver contine o
gama larga de functii de librarie ce pot fi apelate din aplicatia
de programare (Matlab). Aceste functii includ rutine pentru: intrari
analogice (conversie analog-numerica), achizitii de date (conversie
analog-numerica de mare viteza), iesire analogica (conversie numeric-analogica),
generator de forma de unda (conversie numeric-analogica temporizata),
intrari/iesiri digitale, operatii de numarare/temporizare,
auto-calibrare etc.
Windows
XP ca si platforma de instalare a aplicatiilor software.
Instalarea
componentelor necesare:
a.
Instalarea
programului Matlab versiunea 6
Se
introduce CD-ul de instalare in unitatea optica si se ruleaza executabilul
"setup.exe". Este posibil sa se ceara instalarea unei versiuni mai
noi de Java Virtual Machine, asa ca este preferabil ca PC-ul sa fie conectat la
internet pentru instalare, pentru a putea descarca si instala automat update-ul
necasar.
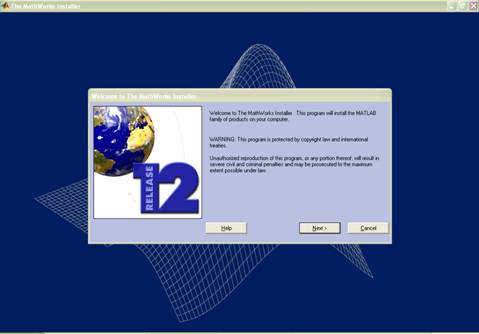
Figura
1.2. Fereastra de instalare pentru Matlab
In
cel de-al doilea dialog se va cere PLP (serialul) pe care il gasim pe
CD-ul de instalare. In lista de produse ce vor fi instalate observam "Data Aquisition Toolbox", un pachet necesar,
dupa cum sugereaza si numele, pentru achizitia de date. In mod normal
acest pachet contine si driverele necesare pentru placa de achizitie
NI-PCI 6110.
Este posibil ca instalarea
propriu-zisa sa dureze cateva minute, odata finalizata instalarea, este
necesara restartarea PC-ului.
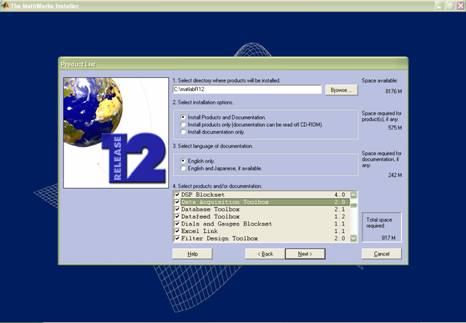
Figura
1.3. Lista de produse ce vor fi instalate
b.
Instalarea
placii de achizitie PCI 6110 si driver-ului NI-DAQ
Instalarea placii presupune instalarea driverelor
primite odatt cu placa si instalarea hardware. Primul pas este instalarea driverelor de pe CD-ul de
instalare, iar ulterior se face instalarea hardware:
Notam numarul
serial al placii 6110 in PCI-6110E/6111E Hardware and Software Configuration
Form in Appendix D, Customer Communication, al manualului de utilizare a placutei.
Se stinge
si se scoate din priza PC-ul.
Se deschide carcasa
PC-ului
Se scoate aparatoarea
slotului
Se
introduce placa 6110 intr-un slot PCI de 5V.
Daca
este necesar se poate insuruba placa de grilajul panoului din spate al
PC-ului
Se inchide carcasa
Se aprinde PC-ul
In
continuare se poate configura din Matlab achizitia de date. Pentru a
verifica instalarea corecta a
placii si recunoasterea acesteia de catre Matlab rulam comanda daqhwinfo('nidaq')in fereastra de comanda, iar rezultatul corect este:
AdaptorDllName:
'C:MATLAB6p6toolboxdaqdaqprivatemwnidaq.dll'
AdaptorDllVersion:
'Version 2.2 (R13) 28-Jun-2002'
AdaptorName: 'nidaq'
BoardNames:
InstalledBoardIds:
ObjectConstructorName:
c.
Instalarea adaptorului BNC-2110
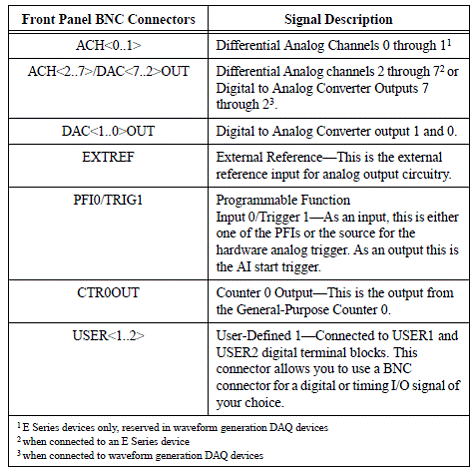
Tabelul 1.4.Descrierea semnalelor adaptorului
BNC-2110
Conectarea
intrarilor analogice
Adaptorul
BNC-21110 poate fi prevazut cu pana la 8 canale diferentiale de intrare
analogica. Conectorii sunt etichetati cu ACH<0..7>. Numarul de conectori
folositi depinde de dispozitivul conectat. BNC-2110 poate fi folosit pentru
masurarea de semnale de intrare flotante sau cu referire la masa. Pentru
masurarea semnalelor surselor flotante, se muta switch-ul localizat sub
conectorul BNC pentru canalul AI folosit. Terminalul negative al
amplificatorului se conecteaza la masa printr-un resistor de 5kW in parallel cu
un condensator de 0,1 uF. Figura
1.5. arata optiunile de configurare a
conectorului BNC.
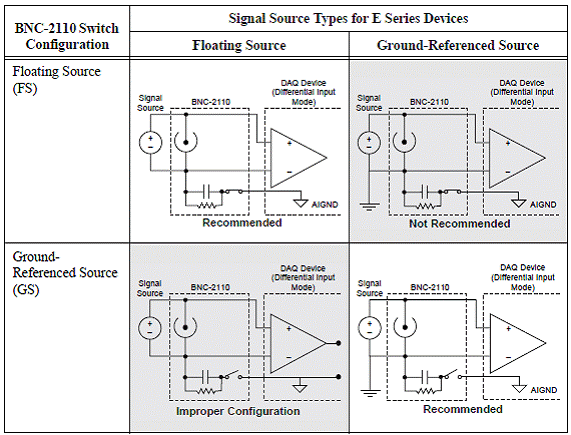
Figura 1.5. Optiunille de configurare a switch-ului
Pentru
masurarea semnalelor de referinta, comutatorul se comuta in pozitia sursa
flotanta sau sursa de referinta. Pentru cea mai buna performanta, se foloseste
pozitia sursa de referinta pentru evitarea buclelor negative.
Conectarea la iesirele analogice
BNC-2110
poate fi pravazut cu pana la 8 canale de conectare pentru iesire diferite.
Acesti conectori sunt etichetati cu DAC<0..7>OUT. Numarul de conectori
folositi depinde de dispozitivul conectat la adaptor. Cand se folosesc
conectorii DAC <7..2>OUT, comutatorul trebuie sa fie in pozitie FS.
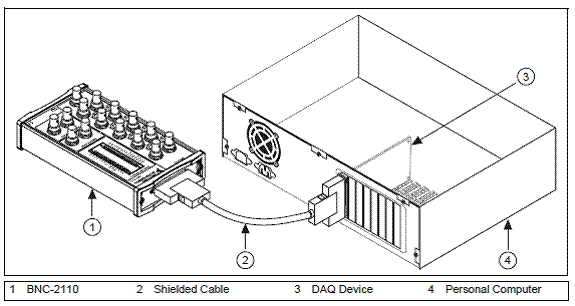
Figura
1.6. Conectarea adaptorului BNC-2110 la placa de achizitie
Placi
de achizitie de date
Introducere
Asocierea
unei placi de achizitie de date cu un calculator il transforma pe acesta din
urma intr-un instrument de masura puternic. In general, din
considerente de pret, placile de achizitie sunt realizate
dupa structura unui sistem de achizitie multicanal cu multiplexarea
semnalelor analogice la intrare (Figura. 2.1).
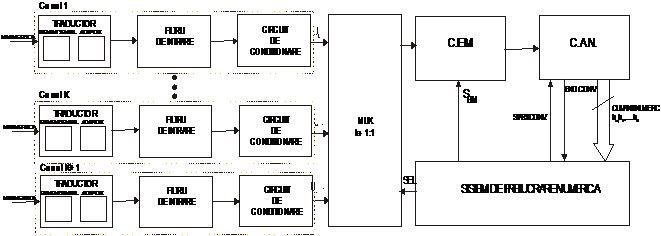
Figura. 2.1 Sistem de
achizitie multicanal
cu multiplexarea semnalelor
analogice la intrare
O
placa de achizitie poate masura pana la 8 semnale analogice bipolare (±5V) sau
unipolare (0 . 10V), provenite dintr-un proces sau dintr-un circuit electronic.
Datorita interferentelor si zgomotelor, in traseele de masurare
se induc tensiuni ce fac ca potentialul acestora sa devieze de la valoarea
de 0 V. Pentru a elimina aceasta eroare de offset, intrarea canalului 0 se
va lega la masa, urmand ca in momentul selectarii acestuia,
potentialul masei sa fie adus la iesire. Acest potential va
fi scazut in permanenta prin soft din potentialele
canalelor selectate.
In urma unei prelucrari analogice (amplificare,
esantionare) semnalele sunt convertite analog-digital si prin
intermediul unei interfete cu calculatorul sunt trimise sub forma unui cod
numeric spre acesta. Calculatorul preia codurile numerice corespunzatoare
marimii urmarite la anumite momente (in functie de
frecventa de esantionare prescrisa) si le prelucreaza
sau le memoreaza pentru o prelucrare ulterioara.
Toate acestea sunt realizate printr-un program
dinainte stabilit in functie de natura parametrilor de proces, de tipul
senzorilor utilizati, sau de gama si forma tensiunilor masurate.
Totodata, calculatorul poate executa si alte operatii, ca de
exemplu operatii intre marimile culese, poate calcula erorile cu care
s-au determinat valorile parametrilor, poate genera pe baza abaterii de la o
valoare prestabilita a acestora, semnale de comanda catre un
sistem de reglare sau semnale de avertizare in cazul depasirii unei
valori limita impuse.
Placa
de achizitie NI-PCI 6110
Acest
subcapitol prezinta functiile de baza ale placii NI-PCI 6110. In figura 2.1
este prezentata schema bloc a acesteia.
Intrari analogice
Sectiunea de intrari analogice pentru placa 611X E
este configurabila prin software. Se pot selecte diferite configuratii de
intrari analogice prin intermediul aplicatiei software. Sectiunile urmatoare
descriu in detaliu fiecare categorie de intrari analogice.
Modul de intare
Placa 611X E
suporta doar intari
diferantiale (DIFF). Configurarea intrarii DIFF ofera pana la patru canale pe
placa PCI-6110E si maxim doua canale pe placa PCI-6111E. Un canal configurat in
modul DIFF utilizeaza doua canale analogice linii de intrare. O linie se
conecteaza la intarea
pozitiva a amplificatorului cu castig al placii
(PGIA), iar cea de-a doua se conecteaza la intrarea negativa a PGIA.
Polaritatea intrarii si gama de intrare
Placa 611X E are doar intrari bipolare. Intrare
bipolara inseamna ca tensiunea de intrare este cuprinsa intre -Vref /2 si + Vref/2. Aceste placi au o gama
de intrare bipolara de 20 V (±10V). Setarile gamei pot fi programate printr-un canal de baza putand
configura fiecare canal de intrare in mod unic. Castigul programabil prin soft
al acestor placi le creste flexibilitatea prin potrivirea gamelor semnalelor de intrare cu
cele suportate de convertorul analog numeric (ADC). Acestea au castig de 0.2,
0.5, 1, 2, 5, 10, 20, si 50 si sunt potrivite pentru gama
larga de niveluri de semnal. Cu
setari corespunzatoare ale castigului, sepoate folosi rezolutia maxima a
convertorului analog-numeric pentru
masurarea semnalului de intrare. In figura 2.2. se
poate vedea gama reala si precizia de masurare in functie de castigul utilizat.
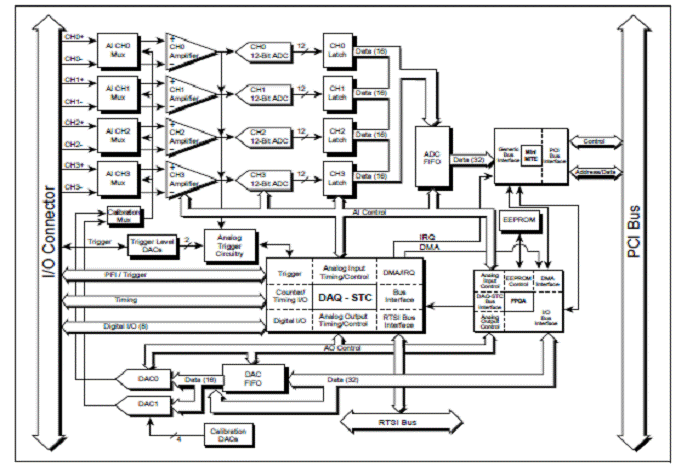
Figura 2.1. Schema bloc a
placii de achizitie NI-PCI 6110.
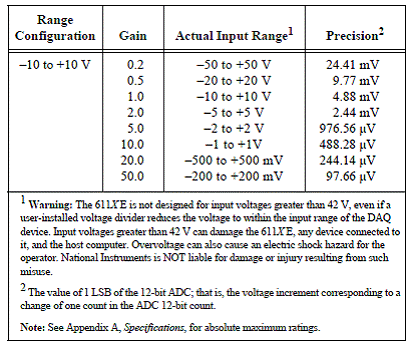
Figura
2.2. Gama reala si precizia de masurare
Consideratii pentru selectarea gamelor de intrare
Gama selectata depinde de gama presupusa a semnalului de
intare. O gama mare de intrare poate cuprinde variatii mari ale semnalului, dar
reduce rezolutia voltajului. Alegand o gama mai mica de intrare se
imbunatateste rezolutia voltajului, dar exista posibilitatea ca semnalul sa
depaseasca gama. Pentru cele mai bune rezultate se incearca alegerea unei game
cat mai apropiata de gama semnalului de intrare.
Cuplarea intrarii
Placa 611X E
poate fi configurata atat pentru intrari
alternative (AC) cat si continue (DC) prin cuplarea la un canal de baza. Se
utilizeaza cuplarea AC cand semnalul AC contine o componenta continua mare. Daca
se activeaza cuplarea AC se elimina offset-ul DC pentru intrarea amplificatorului si se
amplifica doar compoenta alternativa. Astfel
se utilizeaza gama dinamica a convertorului.
Oscilatorul
Oscilatorul adauga aproximativ 0.5 LSBrms de zgomot
alb G semnalului ce va fi convertit de catre ADC. Aceasta adaugare este
folositoare pentru aplicatii ce implica mediatizare pentru cresterea rezolutiei
placii 611X E, cum ar fi calibrarea sau analiza spectrala. In astfelde
aplicatii modulatia zgomotului este decrementata si linearitatea diferentiala
se imbunatateste prin adaugarea oscilatorului. Cand se efectueaza masuratori
DC, cum ar fi verificarea calibrarii placii, sunt necesare o medie de 1000 de
puncte pentru o singura citire Acest proces elimina efectele cuantizarii ai
reduce zgomotul de masurare, rezultand o imbunatatire a rezolutiei.
Iesirea
analogica
Placa
611X E include doua canale analogice de iesire pentru tensiune la
conectorul de intrare/iesire. Gama este fixata bipolar la ±10 V. Aditional pentru sprijinirea declansarilor
sotware-ului intern si a declansarilor digitale externe pentru pornirea
secventei de achizitie de date, aceste placi suporta si declansari analogice.
Circuitul de declansare analogic poae fi configurat sa accepte fie o intrare
analogica directa de la pinul PFI0/TRIG1 al conectorului de intrare/iesire, fie
un semnal postcastig de la iesirea
PGIA la oricare dintre canale. Gama
nivelului declansatorului pentru canalul analogicdirect este ±10 V in pasi de
78 mV pentru placa 611X E. Gama pentru selectia declansatorului
prin post-PGIA este pur si simplu
intreaga gama a a canalului selectat si rezolutia este acea gama impartita la
256.
Intrari/Iesiri
digitale
Placa
611X E contine opt linii de intrari/iesiri digitale pentru orice scop.
Se poate configura individual prin software fiecare linie fie pentru intrare,
fie pentru iesire. La pornirea si resetarea sistemului, toate porturile de
intrare/iesire au impedanta mare.
Controlul
hardware sus/jos pentru numaratoarele 0
si 1 sunt conectate peplaca la DIO6 respectiv DIO7. Astfel DIO6 si DIO7 pot fi utilizate pentru a
controla numaratoarele de scop general Semnalele controlului sus/jos sunt doar
de tipintrare si nu afecteaza operatiile liniilor DIO.
Conectorul
Intrare/Iesire
Figura 2.3 arata asocierea pinilor pentru conectorul
intrare/iesire de 68 de pini al placii 611X E. O descriere a semnalului
urmeaza pentru pinii de iesire ai conectorului.

Figura
2.3.Dispunerea pinilor conectorului de intrare/iesire pe placa NI-PCI 6110
Pentru detalii despre semnalele de
intrare/iesire se poate consulta manualul utilizatorului, tabelul 4-2.
Conexiunile
semnalelor analogice de intrare
Semnalele
de intarare analogice pentru placa 611X
E sunt ACH<0..3>+ si
ACH<0..3>-. Semnalele ACH<0..3>+ sunt rutate la intrarea pozitiva a
PGIA, iar semnalele conectate la ACH<0..3>- sunt rutate la intrarea
negativa a PGIA.
Cu
diversele configuratii, pGIApoate fi utilizat in diverse moduri. Figura 2.4.
arata o diagrama a PGIA continuta de placa 611X E.
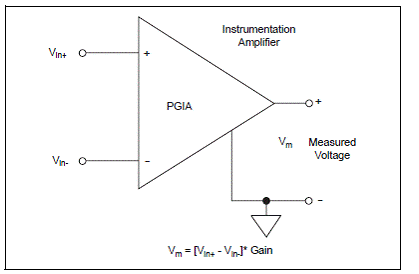
Figura
2.4. Diagrama PGIA
PGIA aplica
castig si rejectia de semnal in mod obisnuit si prezinta impedanta mare de
intrare pentru semnalele analogice de intrare conectate laplaca 611X E.
Semmalele sunt rutate la intrarea pozitiva si la cea negativa a PGIA. PGIA converteste doua semnale de intrare intr-un
singur semnal care este diferenta intre cele doua semnale de intrare inmultita
cu castigul setat al amplificatorului. Tensiunea de iesire a amplificatorului
este conectata la masa pentru placa. Convertorul analog-numeric al placii
masoara aceasta tensiune de iesire cand efectueaza converiile analog-numerice.
Tipuri
de surse de semnal
Cand
se efectueaza conexiunile semnalelor, inprimul rand trebuie determinat daca
sursele de semnal sunt flotante, sau conectate la masa. Sectiunea urmatoare
descrie aceste doua tipuri de semnale.
Surse de semnal flotante
O
sursa flotanta de semnal, nu este conectata la sistemul de impamantare al
cladirii, dar mai de graba are un punct de referinta izolat. Cateva exemple de
surse flotante de semnal ar fi iesirile transformatoarelor, termocuplelor,
dispozitivelor pe baza de baterie, amplificatoare de izolatie. Un instrument
sau dispozitiv care are o iesire izolata este o sursa flotanta de semnal.
Trebuie legata masa unui semnal flotant la placa 611X E masa intrarii analogice pentru a stabili o
referinta locala sau pe placa a semnalului. Semnalul masurat la intrare variaza
atata timp cat sursa depaseste gama modului de intrare setat.
Surse de semnal legate la masa
O
sursa de semnal legata la masa este conectata intr-un fel la sistemul de
impamantare al cladirii si este totodata conectata la masa presupunand ca pc-ul
este conectat la aceasi sursa de curent. Iesirile neizolate a dispozitivelor si
obiectelor sunt introduse in sistemul de alimentare al cladirii intra in
aceasta categorie. Diferenta de potentiall dintre doua dispozitive conectate in
acelasi sistem de alimentare al cladirii este intre 1 si 100mV dar poate fi mai
ridicat daca distributia de current al circuitelor nu este conectata
corespunzator. Daca o sursa de semnal legata la masa este masurata incorect,
aceasta diferenta ar putea da o eroare in masuratori. Instructiunile de
conectare pentru semnale legate la masa sunt gandite pentru a elimina aceasta
diferenta de potential de la semnalul masurat.
Masuratori diferentiale
Se
discuta folosirea masuratorilor diferentiale si consideratiile pentru masurarea
surselor flotante si a celor legate la masa. Figura 2.5. sumarizeaza
conectarile de semnal DIFF si sunt incluse exemple pentru ambele tipuri de
surse.
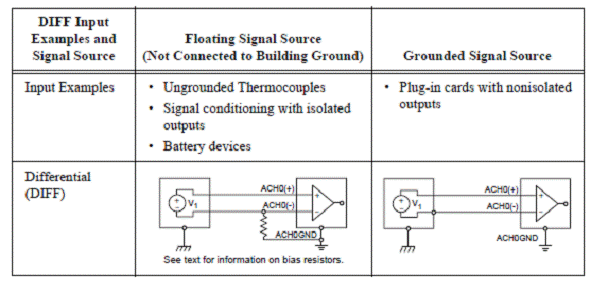
Figura2.5
Tipuri de surse de semnal
Consideratii despre conexiunea
diferentiala
O
conexiune diferentiala este aceea in care semnalul analogic de intrare a placii
611X E are semnalul sau de referinta sau semnalul cale de intoarcere.
Canalele placii 611X E sunt intotdeauna configurate in DIFF mod de
intrare. Semnalul de intrare este legat la semnalul pozitiv a PGIA, care este
un semnal de referinta, sau de intoarcere, este legat la intrarea negativa a
PGIA. Fiecare semnal diferential foloseste doua intrari - una pentru semnal si
una pentru semnalul referinta. Conexiunile de semnal diferential reduc zgomotul
si maresc zgomotul rejectiei de mod comun. Conexiunile de semnal diferential de
asemenea accepta semnale de intrare sa varieze in limitele PGIA.
Conexiuni
diferentiale pentru surse de semnal de referinta legate la masa
Figura
2.6. ne arata cum se conecteaza o sursa de semnal de referinta legata la masa
cu un canal de pe placa 611X E. Cu acest tip de conexiune PGIA rejecta
ambele moduri commune de zgomot din semnal si diferenta de potential dintre
sursa de semnal si masa placii 611X E.
Conexiuni
diferentiale pentru surse de semnal fara referinta sau surse flotante
Figura 2.7. arata cum se conecteaza o sursa de semnal flotanta la un
canal de pe placa 611X E.
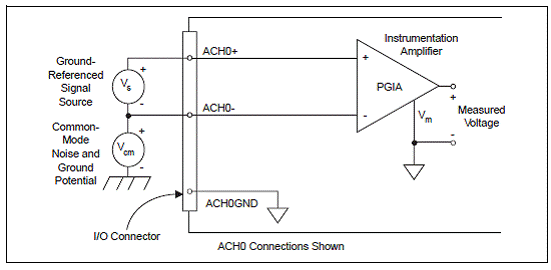
Figura 2.6 Conexiunile
intrarilor diferentiale pentru semnale legate la masa
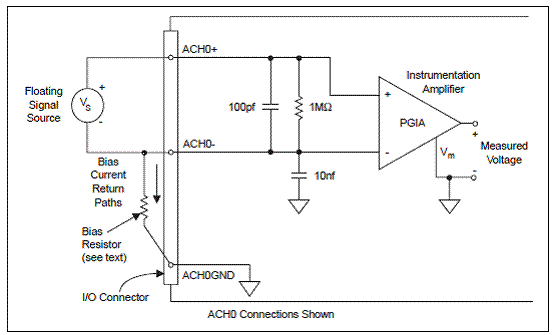
Figura 2.7. Conexiunile
intrarilor diferentiale pentru semnale nelegate la masa
Figura
2.7. ne arata cum se conecteaza un resistor intre ACH0 si sursa de semnal
flotanta legata la masa. Daca rezistorul nu se foloseste si sursa variaza
foarte tare, sursa nu ramane in modul comun a razei de semnal a PGIA, iar PGIA
ajungand la saturatie, creaza erori de citire. Sursa trebuie legata la canalul
corespunzator de masa.
Conexiunile
de temporizare aachizitiei de date
Semnalele
de temporizare a achizitiei de date sunt: SCANCLK, EXTSTROBE*, TRIG1, TRIG2,
STARTSCAN, CONVERT*, AIGATE si SISOURCE. Achizitia de date post-declansata
permite doar vizualizarea datelor achizitionate dupa primirea unui eveniment
declansator. O secvanta de achizitie
post-declansata tipica se poate observa in figura 2.10. Achizitia de date
pre-declansata permite vizualizarea datelor achizitionate inainte de primirea
evenimentului declansator in plus fatade datele achizitionate dupa declansator.
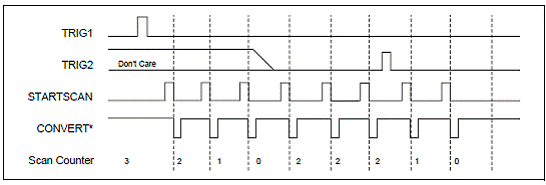
Figura 2.11. prezinta o secventa de
achizitie pre-declansata tipica.
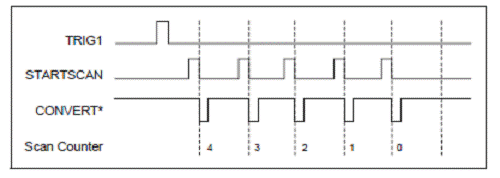
Figura
2.10. Achizitia de date post-declansata tipica
Figura
2.11. Achizitia de date pre-declansata tipica
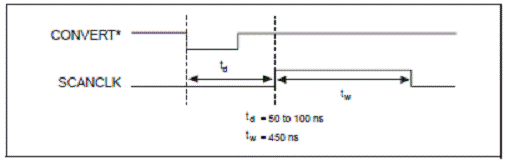
Figura
2.12. Semnalul SCANCLK
Semnalul
SCANCLK
SCANCLK
este un semnal strict de iesire care genereaza un puls cu front crescator la
aproximativ 50 pana la 100 ns dupa ce conversia analog-numerica a inceput.
Polaritatea acestei iesiri este selectabila software, dar in general este
configurata astfel incat un front crescator poate temporiza intrarile analogice
externe multiplexate indicand momentul in care semnalul de intrare a fost
esantionat si poate fi eliminat. Acest semnal are latimea impulsului de 450 ns si este activat software. Figura 2.12.
prrezinta semnalul SCANCLKl.
Semnalul
EXTSTROBE*
EXTSTROBE*
este un semnal strict iesire care genereaza fie un singur impuls sau o secventa
de opt impulsuri in modul hardware-strobe. Un dispozitiv extern poate folosi acest semnal pentru a opri semnale sau declansa
evenimente. In modul un singur impuls, sotware-ul controleaza nivelul
semnalului EXTSTROBE* . Un tact de 10 μs si unul de 1.2 μs sunt
disponibile pentru generarea unei secvente de opt impulsuri in modul
hardware-strobe.

Figura
2.13. Semnalul EXTROBE*
Semnalul
TRIG1
Orice
pin PFI poate primi extern semnalul
TRIG1, care este disponibil ca si iesire la pinul PFI0/TRIG1. Pentru
relationarea semnalului TRIG1 la secventa de achizitie studiati figurile 2.10.
si 2.11. Ca si intrare, semnalul TRIG1
este configurat in modul de detectie a anvelopei. Orice pin PFI poate fi
selectat ca si sursa a semnalului TRIG1 si selectia polaritatii se configureaza
pentru front crescator sau scazator. Frontul selectat pentru semnalul TRIG1 porneste secventa de achizitie de date
atat pentru achizitia post-declansata, cat si pentru cea pre-decalnsata. Placa
611X E accepta declansare analogica prin pinul PFI0/TRIG1. Ca si iesire
TRIG1 reflecta atiunea ce initializeaza secventa de achizitie de date. Aceasta
este valabila chiar daca achizitia este declansata extern prin alt pin PFI.
Iesirea este un impuls activ high cu o latime a pulsului de 25 pana la 50 ns.
Aceasta iesire este setata initial ca si tri-state.
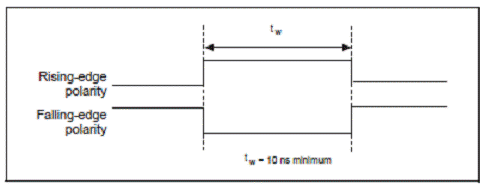
Figura
2.14. Semnalul de intrare TRIG1
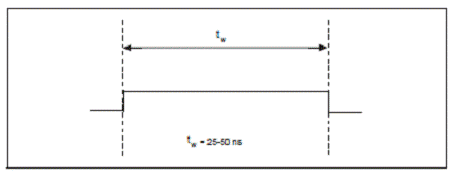
Figura
2.15. Semnalul de iesire TRG1
Placa foloseste semnalul TRIG1 si
pentru a initializa operatiile achizitiei de date pre-declansata. In
majoritatea aplicatiilor pre-declansate, semnalul TRIG1 este generat de un declansator
software.
Semnalul
TRIG2
Orice pin PFI poate primi extern semnalul TRIG2, care
este disponibil ca si iesire la pinul PFI1/TRIG2. Pentru relationarea
semnalului TRIG2 la secventa de achizitie studiati figura 2.11. Ca si intrare,
semnalul TRIG2 este configurat in modul
de detectie a anvelopei. Orice pin PFI poate fi selectat ca si sursa a
semnalului TRIG1 si selectia polaritatii se configureaza pentru front crescator
sau scazator. Frontul selectat pentru semnalul TRIG2 porneste secventa de achizitie de date post-declansata a unei
achizitii pre-decalnsata. In modul pre-declansat, semnalul TRIG1 initializeaza
achizitia de date. Numaratorul de scanare indica numarul minim de scanari
inainte ca TRIG2 sa poata fi recunoscut. Dupa ce numaratorulde scanare ajunge
la zero, este incarcat cu numarulde scanari post-declansate ce trebuiesc
achizitionate cat timp achizitia continua. Placa ignora semnalul TRIG1 daca
este afirmat inainte ca numaratorul de scanare sa ajunga la zero. Dupa
receptionarea frontului selectatalTRIG2, placa va achizitiona un numar fix de
scanari si achizitia se va opri. In acest mod se achizitioneaza date atat
inainte cat si dupa prinirea TRIG2. Ca si iesire, semnalul TRIG2 reflecta
secventa de achizitie post-declansata intr-o secventa deachizitie
pre-declansata. Aceasta este valabila chiar daca achizitia este declansata
extern prin alt pin PFI. Semnalul TRIG2 nu este folosit in achizitia
post-declansata. Iesirea este un impuls activ high cu o latime a pulsului de 25
pana la 50 ns. Aceasta iesire este setata initial ca si tri-state. Figurile
2.16. si 2.17. prezinta semnalul TRIG2.
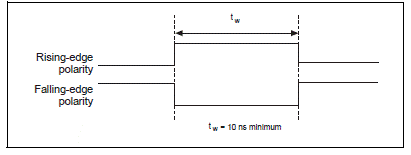
Figura
2.16. Semnalul de intrare TRIG2
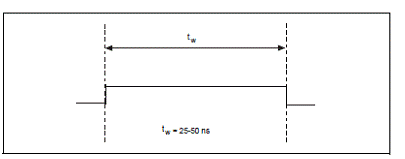
Figura
2.17. Semnalul de iesire TRIG2
Semnalul
STARTSCAN
Orice
pin PFI poate primi extern semnalul STARTSCAN, care este disponibil ca si
iesire la pinul PFI7/ STARTSCAN.
Pentru relationarea semnalului STARTSCAN
la secventa de achizitie studiati figurile 2.10. si 2.11. Ca si intrare,
semnalul STARTSCAN este configurat in modul de detectie a anvelopei. Orice
pin PFI poate fi selectat ca si sursa a semnalului STARTSCAN si selectia polaritatii se configureaza pentru front
crescator sau scazator. Frontul selectat pentru semnalul STARTSCAN initializeaza scanarea. Numaratorul de
intervale de esantionare porneste daca se selecteaza declansarea interna
CONVERT*.
Ca
si iesire semnalul STARTSCAN reflecta impulsul de start al scanarii. Aceasta
este cvalabila chiar daca pornirile sint declansate exterior de catre alt PFI.
Exiata doa optiuni de iesire. Prima este un impuls activ high cu o latime a
pulsului de 25 pana la 50 ns, care indica inceperea scanarii. Cea de-a doua
este un impuls activ high care se
termina la inceputul ultimei conversii in scanare, ceea ce indica o scanare in progres.
Aceasta iesire este setata initial ca si tri-state.
The
AIGATE signal can neither stop a scan in progress nor continue a previously
gated-off scan; in other words, once a scan has started, AIGATE does not gate
off conversions until the beginning of
the next scan and, conversely, if conversions are being gated off, AIGATE does
not
gate them back on until the beginning of the next scan.
SISOURCE
Signal
Any
PFI pin can externally input the SISOURCE signal, which is not available as an
output on the I/O connector. The onboard scan interval counter uses the
SISOURCE signal as a clock to time the generation of the STARTSCAN signal. You
must configure the PFI pin you select as
the
source for the SISOURCE signal in the level-detection mode. You can configure
the polarity selection for the PFI pin for either active high or active low. The
maximum allowed frequency is 20 MHz, with a minimum pulse width of 23 ns high
or low. There is no minimum frequency limitation. Either the 20 MHz or 100 kHz
internal timebase generates the SISOURCE signal unless you select some external
source.
Aplicatie
software pentru achizitia de date si prelucrare
3.1. Introducere despre Matlab
Expresii, Variabile
Intocmai ca majoritatea celorlalte limbaje de programare,
limbajul MATLAB® dispune de expresii matematice, insa, spre deosebire de aceste
limbaje de programare, acestea presupun intregi matrice.
MATLAB nu necesita nici un fel de instructiuni de
declaratii sau de tip.
In momentul in care MATLAB intalneste un nou nume de variabila, va crea in mod
automat variabila si ii va aloca cantitatea adecvata de stocare. Daca variabila
exista deja, MATLAB ii va schimba continutul si, daca este necesar, ii va aloca
un nou spatiu de stocare.
De exemplu:
num_students = 25
Creeaza o matrice de 1ucru numita num_students
si stocheaza valoarea 25 in unicul sau element. Pentru a vizualiza matricea
asignata unei variabile oarecare, introdu pur si simplu numele variabilelor
constau dintr-o litera, urmata de orice numar de litere, cifre, sau
under-score-uri. MATLAB este case sensitive; acesta face distinctia
intre litere majuscule si mici. A si a nu reprezinta aceeasi variabila.
Desi numele de variabile pot avea
orice lungime, MATLAB foloseste numai primele N caractere ale numelui, (acolo
unde N este numarul returnat de catre functia namelengthmax - "lungime
maxima a numelui"), ignorand restul. Prin urmare, este deosebit de important ca
fiecare variabila sa fie unica in intervalul primelor N caractere pentru a-i
permite lui MATLAB sa faca distinctia intre variabile.
N = namelengthmax
N = 63
Functia genvarname poate fi
utila in crearea numelor de variabile care sunt atat valide cat si unice.
Numere
MATLAB foloseste notatii
conventionale in sistem zecimal de numeratie, cu o virgula optionale pentru
zecimale si avand in fata fie semnul plus, fie minus, in cazul numerelor.
Optiunea Scientific notation foloseste litera e pentru a
specifica un factor de scara la puterea a zecea. Numerele complexe - Imaginary
numbers - folosesc fie i, fie j ca sufix. Unele exemple de
numere permise sunt:
3 -99 0.0001
1.60210e-20 6.02252e23
1i -3.14159j 3e5i
Toate numerele sunt stocate intern,
folosind formatul long, specificat de catre standardul de virgula mobila
IEEE®. Numerele cu virgula mobila (flotanta) au o precizie finita de
aproximativ 16 cifre zecimale semnificative si un interval finit de aproximativ
10 la puterea -308 pana la 10 la puterea +308.
Sectiunea "Evitarea problemelor
frecvente care intervin in aritmetica cu virgula mobila" iti prezinta cateva
exemple, aratandu-ti in ce mod afecteaza aritmetica cu virgula mobila IEEE
calculele in MATLAB.
Operatori
Expresiile
folosesc operatori aritmetici cunoscuti si relatii de precedenta.
+ Adunare
- Scadere
* Inmultire
/ Impartire
Impartire la stanga (descrisa in "Algebra liniara", in documentatia MATLAB)
^ Putere
' Transpozitie conjugata complexa
( ) Specifica ordinea de evaluare
Functii
MATLAB furnizeaza un mare numar de
functii matematice elementare, inclusiv abs, sqrt, exp, si sin.
Extragerea radacinii patrate sau logaritmarea unui numar negativ nu sunt
tratate ca erori; rezultatul complex adecvat este returnat automat. MATLAB mai
dispune de numeroase alte functii matematice, inclusiv functiile Bessel
si gamma. Cea mai mare parte a acestor functii accepta argumente
complexe. Pentru o lista a functiilor matematice elementare, apasa
help elfun
help specfun
help elmat.
Unele dintre
functii, precum sqrt si sin, sunt interne - built in.
Functiile interne constituie parte din MATLAB asa ca sunt deosebit de
eficiente, insa detaliile de calcul nu sunt imediat accesibile. Alte functii,
cum ar fi gamma si sinh, sunt implementate in fisiere M.
Exista
anumite diferente intre functiile interne si alte functii. De exemplu, in cazul
functiilor interne, nu poti vizualiza codul. Pentru alte functii, poti vedea
codul si chiar sa il modifici, daca doresti.
Anumite functii speciale furnizeaza valori ale unor
constante utile.
|
pi
|
|
|
i
|
unitate
complexa 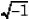
|
|
j
|
la fel ca
i
|
|
eps
|
precizie relativa a virgulei mobile 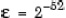
|
|
realmin
|
cel mai mic numar cu virgula mobila
|
|
realmax
|
cel mai mare numar cu virgula mobila 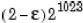
|
|
Inf
|
Infinit
|
|
NaN
|
Not - a -
number (Nu este numar)
|
Valoarea
infinit este generata prin impartira unei valori diferite de 0
la 0, sau de catre evaluarea unor expresii matematice corect definite care sunt
excedentare, adica, care depsesc realmax.
Not-a-number
este generat de incercarea de a evalua expresii cum ar fi 0/0 sau Inf-Inf,
care sunt cazuri de nedeterminare. Numele functiilor nu sunt rezervate. Este
posibila rescrierea oricareia dintre ele cu o noua variabila, cum ar fi si
folosirea apoi a acestei valori in calcule ulterioare. Functia originala poate
fi restaurata cu clear eps
eps = 1.e-6
Exemple de expresii
Deja ai vazut cateva exemple de expresii MATLAB. Iata
inca cateva exemple, precum si valorile rezultante:
rho = (1+sqrt(5))/2
rho = 1.6180
a = abs(3+4i)
a = 5
z = sqrt(besselk(4/3,rho-i))
z = 0.3730+ 0.3214i
huge = exp(log(realmax))
huge =1.7977e+308
toobig = pi*huge
toobig =Inf
Despre matrice
In mediul MATLAB® , o matrice reprezinta
o retea dreptunghiulara de numere. O semnificatie speciala li se atribuie
uneori matricelor 1 la 1, care sunt scalari, si matricelor cu un singura rand
sau coloana, care sunt vectori.
MATLAB dispune si de alte cai de a
stoca atat date numerice cat si nenumerice, insa, la inceput, este cel mai bine
sa gandim totul ca o matrice. Operatiile in MATLAB asunt concepute sa fie cat
mai naturale posibil. Acolo unde alte limbaje de programare lucreaza cu cate un
numar, pe rand, MATLAB iti permite sa lucrezi repede si usor cu intreaga
matrice.
Matrice de intrare
Cel mai potrivit mod de a incepe sa
lucrezi in MATLAB este sa inveti cum sa te manipulezi matricele. Porneste
MATLAB si urmeaza fiecare exemplu.
Poti introduce matrice in MATLAB in mai multe moduri:
. Introdu o lista explicita de elemente.
. Incarca matrice din fisiere extern de date.
. Genereaza matrice folosind functii
interne.
. Creeaza matrice cu propriile tale functii in fisiere M.
Incepe
prin a introduce matricea lui Dürer sub forma unei liste a elementelor sale.
Trebuie doar sa urmezi cateva conventii de baza:
. Separa elementele unui rand prin blank-uri sau prin virgule.
. Foloseste punctul si virgula, ; , pentru a marca sfarsitul
fiecarui rand.
. Incercuieste intreaga lista de elemente cu paranteze
patrate, [ ].
Pentru a introduca matricea lui Dürer, scrie pur si simplu, in fereastra de
comanda,
A = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1]
MATLAB va afisa matricea pe care tocmai
ce ai introdus-o:
A = 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
Odata ce
ai introdus matricea, ea va fi in mod automat memorata in spatiul de lucru al
MATLAB. Poti face referire la ea numind-o pur si simplu A. Acum ca il ai pe A
in spatiul tau de lucru, arunca o privire la ce anume o face atat de
interesanta. De ce este ea magica?
sum, transpose, si diag
Probabil deja incepi sa iti dai seama ca
proprietatile speciale ale unui patrat magic au legatura cu numeroasele moduri
de a-i aduna elementele. Daca iei suma de pe oricare rand sau coloana, sau cea
de pe oricare dintre cele doua diagonale principale. Vei obtine de fiecare data
acelasi numar. Sa verificam acest lucru folosind MATLAB. Prima instructiune pe
care o vom incerca este:
sum(A)
MATLAB raspunde cu:
ans = 34 34 34 34
Atunci cand nu specifici o variabila de
iesire, MATLAB foloseste variabila ans, prescurtare de la answer,
pentru a stoca rezultatele unui calcul. Ai calculat un vector rand, care contine
sumele coloanelor lui A. Este clar ca elementele de pe fiecare coloana
insumeaza aceeasi valoare, suma magica, 34.
Dar
sumele de pe randuri? MATLAB are o preferinta pentru lucrul cu coloanele unei
matrice, asa ca, o modalitate de a obtine sumele de pe randuri este aceea de a
transpune matricea, de a calcula apoi sumele de pe coloane ale transpusei, si,
in cele din urma, transpunerea rezultatului. Pentru a alege o alta cale, prin
care se evita dubla actiune de transpunere, foloseste argumentul dimensiune
pentru functia sum.
MATLAB
are dispune de doi operatori de transpunere. Operatorul apostrof (de
exemplu, A') efectueaza o transpozitie conjugata complexa. Aceasta inverseaza o
matrice dupa diagonala sa principala, si schimba de asemenea si semnul componentei
imaginare a oricarui element complex al matricei. Operatorul punct-apostrof (de
exemplu, A.'), transpune fara a afecta semnul elementelor complexe. Pentru
matricele care nu contin ca elemente decat numere reale, ambii operatori
returneaza acelasi rezultat.
Astfel, A' produce:
ans = 16 5 9 4 3 10 6 15 2 11 7 14 13 8 12 1
,iar
sum(A')'
produce un vector-coloana care contine
sumele de pe fiecare rand
ans = 34 34 34 34
Suma elementelor de pe diagonala
principala se obtine cu ajutorul functiilor sum si diag:
diag(A)
produce rezultatul
ans = 16 10 7 1
iar
sum(diag(A))
produce
ans = 34
Cealalta diagonala, asa-numita antidiagonala,
nu este atat de importanta din punct de vedere matematic, asa ca MATLAB nu
are o functie gata configurata pentru aceasta. Insa exista o functie care a
fost initial destinata utilizarii in programele de grafica, fliplr, care
intoarce o matrice de la stanga spre dreapta:
sum(diag(fliplr(A))) ans = 34
Ai
verificat daca matricea din gravura lui Dürer este intr-adevar un patrat magic,
si, in decursul procesului, ai incercat si cateva operatii MATLAB asupra
matricei. Urmatoarele sectiuni continua sa foloseasca aceasta matrice pentru a
ilustra capacitati suplimentare ale MATLAB.
Subscripturi
Elementul de pe randul i si de pe
coloana j a lui A este denotat prin notatia A(i,j). De exemplu, A(4,2) este
numarul de pe al patrulea rand si de pe a doua coloana. Pentru patratul nostru
magic, A(4,2) este 15. Asa ca, pentru a calcula suma elementelor de pe a patra
coloana a lui A, scrie
A(1,4) + A(2,4) + A(3,4) + A(4,4)
Astfel vei obtine
ans = 34
insa acesta nu reprezinta cea mai
eleganta modalitate de a insuma o coloana. Ne putem referi la elementele unei
matrice cu un singur subscript, A(k). Acesta este modul uzual de a ne
referi la vectorii rand si coloana. Insa, se poate aplica de asemenea si la o
matrice in totalitate bidimensionala, caz in care aranjamentul este considerat
ca fiind un vector-coloana lung, format din coloanele matricei originale. Asa
ca, pentru patratul nostru magic, A(8) reprezinta o alta modalitate de a ne
referi la valoarea 15 stocata in A(4,2).
Daca
incerci sa folosesti valoarea unui element in afara matricei, se va returna o
eroare:
t = A(4,5)
Indicele depaseste dimensiunile
matricei. Pe de alta parte, daca stochezi o valoare intr-un element din afara
matricei, dimensiunea creste pentru a primi noul venit:
X = A; X(4,5) = 17 X = 16 3 2 13 0 5 10 11 8 0 9 6 7 12 0 4 15 14 1 17
Operatorul ":"
Semnul ortografic "doua puncte", :,
constituie unul dintre cei mai importanti operatori MATLAB. El intervine sub
diverse forme. Expresia 1:10 intr-un vector orizontal care contine numere
intregi cuprinse in intervalul1 - 10:
1 2 3 4 5 6 7 8 9 10
Pentru a obtine o un interval nonunitar,
specica un spor de crestere. De exemplu,
este
100 93 86 79 72 65 58 51
si
0:pi/4:pi
este
0 0.7854 1.5708 2.3562 3.1416
Expresiile subscript care implica
coloane se refera la portiuni apartinand unei matrice:
A(1:k,j)
inseamna primele k elemente din coloana
j a lui A. Asa ca
sum(A(1:4,4))
calculeaza suma elementelor din a patra
coloana. Insa exista o cale mai buna. Coloana se refera ea insasi la toateelementele
de pe un rand sau de pe o coloanaa unei matrice, iar cuvantul cheie end se
refera la ultimul rand sau la ultima coloana. Asa ca
sum(A(:,end))
calculeaza suma elementelor de pe ultima
coloana a lui A:
ans = 34
De ce este suma magica a unui patrat
4-cu-4 egala cu 34? Daca numerele intregi de la 1 la 16 sunt sortate in patru
grupuri cu sume egale, acea suma trebuie sa fie
sum(1:16)/4
care, desigur, este
ans = 34
Functia magica
De fapt, MATLAB dispune de o functie
interna care creeaza patrate magice de aproape orice dimensiune. Deloc
surprinzator, aceata functie este denumita magic:
B = magic(4) B = 16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1
Aceasta matrice este aproape identica cu
cea din gravura lui Dürer si are celeasi proprietati "magice"; singura
diferenta este aceea ca cele doua coloane din mijloc sunt interschimbate.
Pentru a face aceasta matrice B sa se transforme in matricea A a lui Dürer,
interschimba cele doua coloane din mijloc:
A = B(:,[1 3 2 4])
Aceasta spune ca, pentru fiecare dintre
randurile matricei B, se reordoneaza elementele in ordinea 1, 3, 2, 4. Va
rezulta:
A = 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1
Crearea unui grafic
Tipul de grafic pe care vrei sa-l creezi
depinde de natura datelor tale si de ceea ce vrei sa evidentiezi prin analiza
lor. Poti alege din mai multe tipuri predefinite de grafice, cum ar fi linie,
bara, histograma, 'placinta', dar si grafice 3-D cum ar fi:
suprafete, planuri sectionate, etc.
Exista 2 metode elementare prin care poti crea grafice in MATLAB:
Interactiv, folosind tool-uri
de trasare a graficelor (plotting);
Prin intermediul
instructiunilor introduse in fereastra de comenzi (Command Window).
E posibil sa consideri utila imbinarea
celor doua abordari. De exemplu, poti scrie o comanda pentru a crea un grafic,
modificandu-l apoi cu ajutorul tool-urilor interactive.
Explorarea datelor
Dupa ce ai creat un grafic, poti extrage
anumite informatii legate de date, cum ar fi valoarea numerica a unui varf din
grafic sau valoarea medie a unei serii de valori, sau poti afisa informatii
suplimentare folosind Data tips si tool-uri Data brushing.
Editarea componentelor
Graficele sunt compuse din obiecte ce au
proprietati pe care le poti schimba. Aceste proprietati afecteaza modul in care
diferitele componente ale graficului arata si se comporta. De exemplu, axele ce
definesc sistemul de coordonare au proprietati ce definesc limitele fiecarei
axe, scara, culoarea, etc. Linia folosita pentru a crea un grafic de tip linie
are proprietati cum ar fi culoarea, tipul de marker pentru a identifica fiecare
valoare, etc.
N.B.
Valorile datelor pe care un grafic de
tip linie le afiseaza sunt copiate si devin proprietati ale obiectului grafic.
Astfel, poti adauga valori sau poti modifica valorile deja existente fara a
crea un nou grafic.
Adnotarea
Adnotarile reprezinta textul, sagetile
si alte etichete adaugate graficelor pentru a scoate in evidenta anumite date
importante pentru utilizatori. De obicei se adauga adnotari atunci cand doresti
sa arati graficele altor persoane sau daca vrei sa le pastrezi pentru a le
utiliza pe viitor.
Printarea si exportarea graficelor
Iti poti lista graficul la orice
imprimanta conectata la PC-ul tau. Cu optiunea print preview poti vedea cum va
arata el cand va fi printat si poti adauga headere, footere, o data s.a.m.d.
Casuta print preview iti permite sa controlezi marimea, asezarea si alte
caracteristici ale graficului (selecteaza Print Preview din meniul File).
Exportarea unui grafic consta in crearea
unei copii intr-un format standard de fisier imagine, cum ar fi TIFF, JPEG sau
EPS. Apoi poti introduce fisierul intr-un procesor word, il poti include
intr-un document HTML sau il poti modifica intr-un program de editare de
imagini (selecteaza Export Setup din meniul File).
Adaugarea si stergerea figurilor
Cand creezi un nou grafic in aceeasi
fereastra, datele sale le inlocuiesc pe cele ale graficului afisat anterior,
daca exista vreunul. Poti sterge toate datele, grafica si adnotarile din
imaginea curenta prin tastarea comenzii CLF in linie de comanda sau prin
selectarea optiunii Clear Figure din meniul Edit.
Salvarea graficelor
Exista 2 metode prin care poti salva un
grafic, astfel incat sa il poti reutiliza pe viitor:
Ca fisier FIG (selectand Save
din meniul File)
Generand codul MATLAB care
poate recrea graficul (selecteaza Generate M-File din meniul File).
Fisierele FIG sunt fisiere in format
binar care salveaza o figura in stadiul ei curent, ceea ce inseamna ca toate
obiectele de tip grafic si setarile lor sunt stocate in fisier atunci cand
acesta este creat. Fisierul poate fi redeschis intr-o alta sesiune MATLAB,
chiar daca il rulezi pe un alt computer. Cand incarci un fisier FIG, o noua
imagine MATLAB se deschide in acelasi stadiu ca si cea pe care ai salvat-o.
N.B.
Setarile tool-urilor din bara de meniu
nu se salveaza in fisierul FIG; doar continutul graficului si adnotarile sale
sunt salvate. Continuturile data tips-urilor (create cu Data Cursor)
sunt si ele salvate. Asta inseamna ca fisierele FIG se deschid intotdeauna in
modul default.
Codul generat
Poti folosi generatorul MATLAB M-code
pentru a crea un cod care reconstruieste graficul. Spre deosebire de fisierul
FIG, codul generat nu contine vreo informatie; in schimb, trebuie sa transmiti
datele corespunzatoare functiei generate atunci cand rulezi codul. Daca
studiezi codul generat pentru un grafic poti invata cum sa programezi folosind
MATLAB.
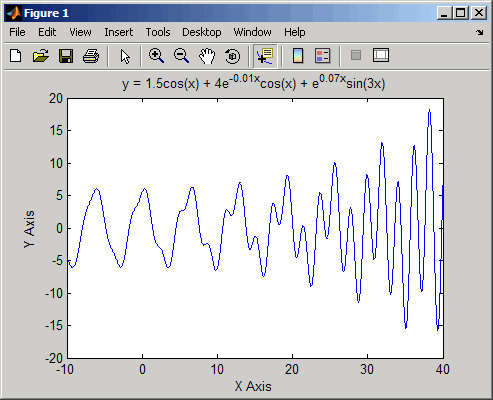
Componentele unui grafic
Graficele MATLAB sunt afisate intr-o
fereastra cu titlul 'Figure 1'. Pentru a crea un grafic trebuie sa
definesti un sistem de coordonate. Astfel, fiecare grafic este plasat in cadrul
unor axe care sunt continute de fereastra.
Poti obtine reprezentarea vizuala a
datelor cu ajutorul unor grafice de tip linie si suprafata. Acestea sunt
desenate in cadrul sistemului de coordonate, definit de axe ce apar automat
pentru a mari intervalul de valori. Datele propriu zise sunt stocate ca
proprietati ale obiectelor de tip grafic. Imaginea urmatoare arata componentele
de baza ale unui grafic tipic.
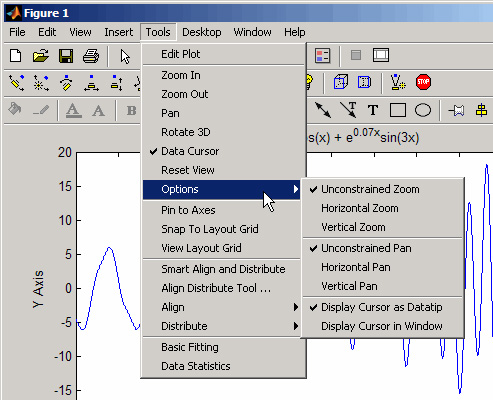
Tool-urile ferestrei
Fereastra contine un set de tool-uri
care opereaza asupra graficelor. Acestea pot fi accesate prin intermediul
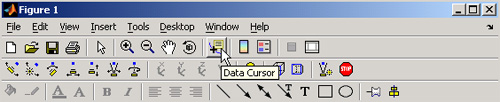
meniului Tools, dupa cum se poate observa din figura de mai jos. Tot in imaginea de mai jos pot fi observate 3 bare de meniu,
ce sunt discutate in sectiunea "Toolbars".
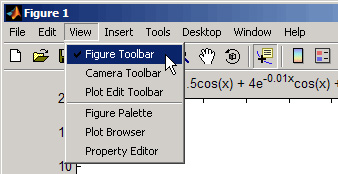
Cum se acceseaza diversele optiuni
Poti accesa sau retrage diferite
toolbar-uri si alte tool-uri din meniul View, de unde poti activa si
dezactiva elementele de care ai nevoie. Un toolbar nou adaugat va fi afisat sub
cel aflat in partea cea mai de jos.
Toolbar-uri pentru figura (Figure Tools)
Aceste toolbar-uri ofera un acces facil
la mai multe optiuni de modificare a graficului. Ceea ce trebuie sa retii este
ca exista 3 bare de meniu de acest tip. Daca asezi cursorul pe un buton anume,
vei vedea un scurt text care iti indica functia butonului respectiv. In
urmatoarea imagine poti vedea cele 3 bare de meniu, avand cursorul plasat pe
functia Data Cursor.
Toolbar-uri pentru trasarea graficelor
(Plotting Tools)
Aceste functii sunt atasate figurilor si
te ajuta la trasarea graficelor. Ele iti permit
sa realizezi urmatoarele sarcini:
Sa selectezi tipul de grafic
(linie, bara, suprafata,etc.)
Sa modifici variabila ce
reprezinta tipul de grafic
Sa vizualizezi si sa setezi
proprietatile obiectelor de tip grafic
Sa adnotezi graficele folosind
texte, sageti, etc.
Sa creezi si sa aranjezi
sub-graficele in figura
Sa stergi si sa introduci noi
valori in setul de date initial
Poti afisa aceste tool-uri din meniul View
sau dand click pe iconita Show PlotTools din bara de meniu,
dupa cum se arata in imaginea urmatoare.
De asemenea, ele pot fi activate si din
linia de comanda, cu ajutorul instructiunii plottools.
Tool-urile de tip plotting sunt
alcatuite din 3 componente GUI independente:
Figure Palette
- specifica si ordoneaza sub-graficele, acceseaza variabilele spatiului de
lucru pentru trasarea graficelor sau editare si adauga adnotari.
Plot Browser
- selecteaza obiectele din ierarhia de grafice, controleaza vizibilitatea si
adauga valori axelor de coordonate
Property Editor
- schimba proprietatile cheie ale obiectului selectat. Da click pe More
Properties pentru a accesa toate proprietatile obiectului cu Property
Inspector
De asemenea, poti controla aceste
componente din linia de comanda prin tastarea urmatoarelor instructiuni:
figurepalette
plotbrowser
propertyeditor.
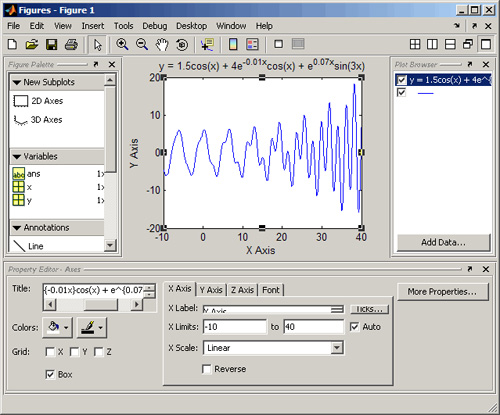
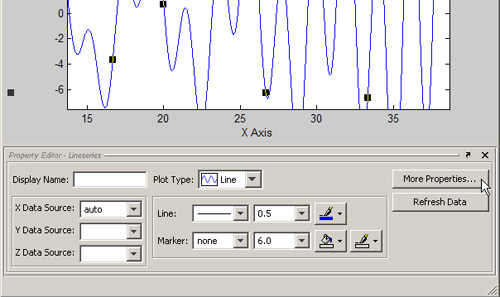
Urmatoarea imagine arata o figura avand
activate toate cele trei ferestre:
Folosirea tool-urilor si a codului
MATLAB
Poti activa tool-urile de tip plotting
pentru orice grafic, chiar si pentru unul creat prin folosirea comenzilor
MATLAB. De exemplu, sa presupunem ca ai tastat urmatorul cod pentru a trasa un
grafic:
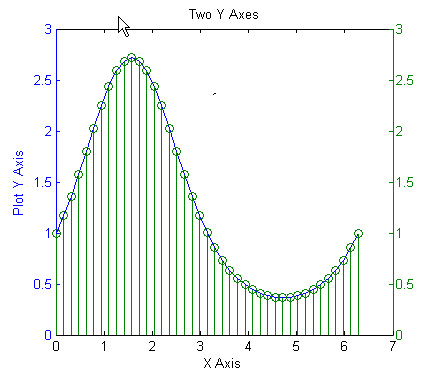
t = 0:pi/20:2*pi; y = exp(sin(t)); plotyy(t,y,t,y,'plot','stem') xlabel('X Axis') ylabel('Plot Y Axis') title('Two Y Axes')
Acest grafic contine 2 axe y, prima pentru
graficul de tip linie (albastru), si cea de-a doua pentru graficul format din
linii verticale (verde). Cu ajutorul tool-urilor de tip plotting poti selecta
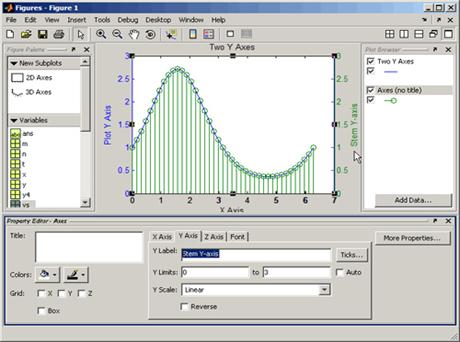
orice obiect din grafic si ii poti edita proprietatile. De exemplu, adaugarea
unei etichete pentru axa y care corespunde graficului trasat cu verde se
realizeaza usor prin selectarea acelei axe din Plot Browser si setarea
proprietatii Y Label in Property Editor (daca nu vezi textul,
mareste fereastra pentru a o face mai inalta).
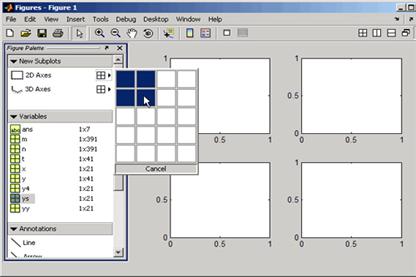
Aranjarea mai multor grafice pe aceeasi
figura
Poti afisa un anumit numar de axe intr-o
figura prin selectarea layout-ului dorit din meniul Figure Palette. De
exemplu, urmatoarea imagine iti arata cum sa afisezi 4 axe 2-D in aceeasi
fereastra.
Selecteaza axele pe care vrei sa le
folosesti pentru trasarea graficului. Ca si alternativa, poti folosi functia subplot
pentru a crea mai multe axe.
Alegerea modului de desenare a
graficului
Diferitele tipuri de grafice 2-D si 3-D
sunt descrise in "Types of MATLAB Plots" din documentatia MATLAB Graphics.
Aproape orice tip de grafice este descris si exemplificat de catre tool-ul Plot
Catalog. Poti folosi aceasta optiune pentru a vizualiza diferitele
modalitati de desenare, pentru a alege una care sa reprezinte cat mai bine
variabilele selectate de tine si, in final, pentru a o aplica figurii curente
sau unei figuri nou create. Plot Catalog poate fi accesat prin
selectarea uneia sau mai multor variabile dupa cum urmeaza:
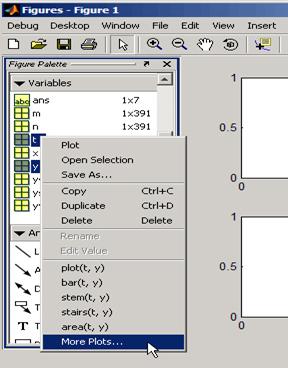
In Figure Palette da
click dreapta pe o variabila selectata si, din meniul care apare, alege
optiunea More Plots;
In browser-ul spatiului de
lucru, da click dreapta pe o variabila selectata si alege More Plots din
meniu, sau apasa butonul Plot selector si alege More Plots
din meniul sau.
In editorul de variabile (Variable
Editor) selecteaza valorile pentru care vrei sa trasezi graficul, da click
pe Plot selector si alege More Plots din meniul sau.
Iconita butonului Plot selector
reprezinta un tip de grafic si se schimba in functie de tipul datei pe care o
selectezi. Ea este dezactivata daca tipul datelor selectate nu este numeric,
sau nu a fost selectata nici o variabila. Urmatoarea imagine iti arata cum poti
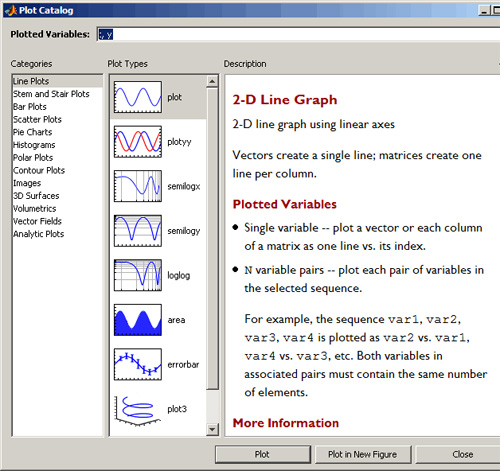
deschide Plot Catalog din Figure Pallette:
Dupa ce selectezi un mod de desenare si
dai click pe Plot sau Plot in New Figure, intr-o fereastra noua
se va deschide Plot Catalog-ul, avand variabilele selectate pregatite
pentru trasarea graficului. Cu ajutorul campului Plotted Variables, poti
inlocui variabilele selectate initial cu alte nume de variabile sau expresii
MATLAB
Modul de editare (Plot Edit Mode)
Modul de editare al unei diagrame in
Matlab iti permite sa selectezi anumite obiecte dintr-un grafic si te ajuta in
modificarea multora dintre ele. Pentru a activa aceasta modalitate de editare,
trebuie sa dai click pe sageata din toolbar.
Ca alternativa, poti selecta si optiunea
Edit Plot din meniul Tools.
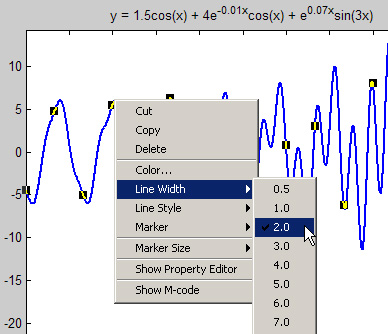
Setarea proprietatilor obiectului
Dupa ce ai activat modul de editare,
poti selecta obiectele din graphic printr-un simplu click. Pentru a selecta mai
multe obiecte, tine apasata tasta Shift. Avand cursorul deasupra
obiectului selectat, da click dreapta pentru a-i afisa meniul context:
Acest meniu iti ofera un acces rapid la
cele mai des folosite operatii si proprietati.
Folosirea editorului de proprietati
Avand activat modul de editare, un dublu
click pe un obiect din diagrama va deschide editorul de proprietati (Property
Editor), cu ajutorul caruia sunt afisate proprietatile importante ale
acelui obiect. Property Editor ofera acces la cele mai uzuale
proprietati ale obiectului. In momentul in care selectezi un obiect, editorul
este actualizat pentru a expune proprietatile obiectului ales.
Accesarea proprietatilor cu Property
Inspector
Property Inspector este o functie care iti permite sa
accesezi majoritatea proprietatilor de manipulare a graficelor (Handle
Graphics) si alte obiecte MATLAB. Daca nu gasesti proprietatea pe care vrei sa o modifici in Property
Editor, da click pe optiunea More Properties pentru a activa Property
Inspector. Poti folosi si comanda inspect pentru a porni aceasta
optiune. De exemplu, pentru a vizualiza proprietatile axelor curente tasteaza: inspect(gca).
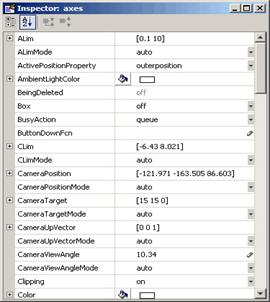
Imaginea urmatoare ilustreaza felul in
care Property Inspector afiseaza proprietatile axelor unui grafic. El
enumera fiecare proprietate si ofera un text sau un alt instrument
corespunzator cu ajutorul caruia poti seta valoarea proprietatii. Pe masura ce
selectezi diferite obiecte, Property Inspector este actualizat pentru a
afisa proprietatile obiectului curent.
In mod implicit, Property Inspector
enumera proprietatile in ordine alfabetica. Cu toate acestea, poti grupa
obiectele de tip Handle Graphics, cum ar fi axele de coordonate, dupa categorii
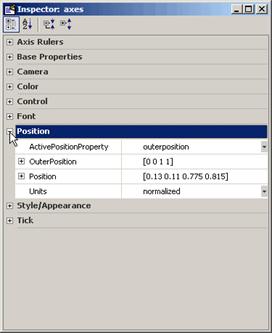
pe care le poti activa sau inchide in Property Inspector. Pentru a face acest lucru, da click pe
iconita din partea de sus stanga, apoi pe semnul + pentru categoria pe
care vrei sa o extinzi. De exemplu, pentru a vedea proprietatile legate de
pozitie, da click pe semnul + din stanga categoriei Position.
Aceasta categorie se va deschide, iar +
se modifica in - pentru a indica ca poti inchide optiunea dand click pe ea.
Folosirea functiilor pentru a edita
graficele
Daca preferi sa lucrezi din linia de
comanda MATLAB, sau daca vrei sa creezi un fisier M, poti folosi comenzile
MATLAB pentru a edita un grafic. Cu ajutorul comenzilor set si get
poti modifica proprietatile obiectelor dintr-un grafic.
3.2.
Achizitia unui semnal folosind placa de achizitie NI PCI-6110
Matlab suporta seria M,
E si hardware USB de la National Instruments prin intermediul Data Acquisition
Toolbox. Urmatorul exemplu de cod demonstreaza cum se pot achizitiona si
analiza date de la hardware-ul National Instruments in 10 comenzi. Comenzi
aditionale care pot fi utile sunt deasemenea ilustrate.
Aceasta comanda se foloseste pentru
determinarea ID-ului placii conectate la
sistem PCI-6110
hw = daqhwinfo('nidaq')
hw.InstalledBoardIds hw.BoardNames
Conform partii introductive a acestui proiect,
inca de la instalarea placii de achizitie PCI-6110, la rularea comenzii: daqhwinfo('nidaq')in fereastra de comanda, rezultatul corect este:
AdaptorDllName: 'C:MATLAB6p6toolboxdaqdaqprivatemwnidaq.dll'
AdaptorDllVersion:
'Version 2.2 (R13) 28-Jun-2002'
AdaptorName:
'nidaq'
BoardNames:
InstalledBoardIds:
ObjectConstructorName:
Deci ID-ul placii va fi: '1'. Crearea unui obiect de intrare analogica folosind ID-ul de placa "Dev6" ai = analoginput('nidaq','Dev6');
Achizitia de date se face de la canalul 3 al placii: addchannel(ai, 3);
Pentru a vizualiza configuratia de baza a achizitiei se tipareste numele variabilei : ai Pentru a vedea proprietatile ce pot fi configurate: set(ai) Pentru a vedea o lista cu toate proprietatile obiectului si setarile lor curente: get(ai) Configurarea intrarilor analogice in mod singular sau diferntial: set(ai,'InputType','SingleEnded');
set(ai,'InputType','Differential');
Configurarea frecventei de esantionare: ai.SampleRate = 10000;
ai.SamplesPerTrigger = 10000;
Incepe achizitia: start(ai);
Asteapta 2 secunde pentru finalizarea achizitiei wait(ai,2);
Achizitioneaza datele in spatiul de lucru al Matlab data = getdata(ai);
Afiseaza grafic rezultatele plot(data); Sterge tot stop(ai);
delete(ai);
Astfel, programul pentru achizitie de
semnal folosind placa de achizitie NI PCI-6110 este:
Program Matlab pentru achizitie de semnal
|
% Folosind placa de achizitie NI PCI-6110
ai = analoginput('nidaq',1);
addchannel(ai, 3);
ai.SampleRate = 10000;
ai.SamplesPerTrigger = 10000;
start(ai);
wait(ai,2);
data = getdata(ai);
plot(data);
stop(ai);
delete(ai);
|
3.3. Simularea unui semnal de alimentare perturbat si filtrarea acestuia
FILTDEM Exemplu de creare a unui filtru si filtrarea semnalului.
Acest exemplu creaza un filtru cu Signal
Processing Toolbox si il aplica unui
semnal alcatuit din componente armonice.
Program Matlab pentru filtrare de semnal
|
% Folosind Signal Processing Toolbox
Fs=100; %
Frecventa
t=(1:100)/Fs;
s1=sin(2*pi*t*5); % Cele
3 componente armonice
s2=sin(2*pi*t*15);
s3=sin(2*pi*t*30);
s=s1+s2+s3; %
Semnalul ce va fi filtrat
plot(t,s); % Se
afiseaza semnalul
xlabel(''Time (seconds)'');
ylabel(''Time waveform'');
[b,a]=ellip(4,0.1,40,[10 20]*2/Fs); % Creaza filtrul
[H,w]=freqz(b,a,512);
plot(w*Fs/(2*pi),abs(H)); % Afiseaza filtrul
xlabel(''Frequency (Hz)'');
ylabel(''Mag. of frequency response'');
sf=filter(b,a,s); % Se
filtreaza semnalul
plot(t,sf); % Se
afiseaza semnalul filtrat
xlabel(''Time (seconds)'');
ylabel(''Time waveform'');
axis([0 1 -1 1]);
|
3.3.1.
Tranformata Fourier discreta
Pentru determinarea transformatei
Fourier discreta Matlab dispune de functia predefinita "fft()" care poate fi aplicata direct asupra
semnalului caruia dorim sa ii aflam transformata Fourier, iar valoarea
returnata de functie este chiar aceasta. Considerand exemplul anterior, pentru
a determina transformatele Fourier pentru semnalul de intrare si pentru cel filtrat, este suficienta
urmatoarea secventa:
S=fft(s,512); % Transformata
Fourier discreta
SF=fft(sf,512); % pentru
semnalul initial si filtrat
Pentru
utilizator este chiar mai complexa afisarea transformatei, decat calculul
acesteia.
Pentru a afisa cele doua semnale rezultate din
secventa de mai sus:
w=(0:255)/256*(Fs/2);
plot(w,abs([S(1:256)'' SF(1:256)'']));
xlabel(''Frequency (Hz)'');
ylabel(''Mag. of Fourier transform'');
3.3.2.
Prezentare program
In aceasta sectiune se incerca
reunirea tuturor secventelor descrise anterior intr-un singur program.
Program care efectueaza achizitia de
semnal prin intermediul placii deachizitie PCI-6110, afiseaza semnalul
achizitionat, il "perturbeaza" adaugandu-i doua componente armonice de 5 si 30
Hz, pe care le eliminam prin aplicarea unui filtru trece-banda si vizualizam
transformata Fourier discreta a semnalului achizitionat, semnalului perturbat
si a semnalului filtrat pentru concluzii.
Programul
rezultat poate fi considerat un demo, fiind obtinut prin reunirea de secvente
de cod descrise in diverse tutoriale de Matlab, unele se regasesc chiar in
help-ul Matlab-ului.
Program Matlab de achizitie, filtrare, transformare Fourier
|
% Folosind placa de achizitie NI PCI-6110
% si Signal Processing Toolbox
ai = analoginput('nidaq',1);
addchannel(ai, 3);
ai.SampleRate = 10000;
ai.SamplesPerTrigger = 10000;
start(ai);
wait(ai,2);
data = getdata(ai);
plot(data);
stop(ai);
delete(ai);
Fs=100;
t=(1:100)/Fs;
s1=sin(2*pi*t*5);
s3=sin(2*pi*t*30);
s=s1+s2+data;
plot(t,s);
xlabel(''Time
(seconds)'');
ylabel(''Time
waveform'');
[b,a]=ellip(4,0.1,40,[10 20]*2/Fs);
[H,w]=freqz(b,a,512);
plot(w*Fs/(2*pi),abs(H));
xlabel(''Frequency
(Hz)'');
ylabel(''Mag. of
frequency response'');
sf=filter(b,a,s);
plot(t,sf);
xlabel(''Time
(seconds)'');
ylabel(''Time
waveform'');
axis([0 1 -1 1]);
S=fft(s,512);
SF=fft(sf,512);
w=(0:255)/256*(Fs/2);
plot(w,abs([S(1:256)'' SF(1:256)'']));
xlabel(''Frequency
(Hz)'');
ylabel(''Mag. of
Fourier transform'');
|
Bibliografie
[1] https://www.e-learn.ro/tutorial_details/APLICATII_DEDICATE/Matlab
[2] PCI-6110 & 6111
Specification Corrections
[3] PCI-6110E and PCI-6111E
User Manual
[4] BNC-2110 Installation Guide
[5] https://www.ni.com/dataacquisition/software/
[6] https://www.ni.com/pdf/products
[7] Matlab - help
[8] https://www.mathworks.com/access/helpdesk/help/toolbox/daq/