MANAGEMENTUL PROIECTELOR - EXCEL
Managementul proiectelor
Multe
din proiectele din viata reala sunt foarte complexe si
costisitoare. Realizarea acestora la timp si in cadrul bugetului alocat nu
este o sarcina usoara. In mod tipic, anumite
activitati nu pot incepe inainte ca altele sa se termine. Iar
daca intr-un proiect apar sute de astfel de dependente, problemele de
planificare se complica foarte mult, iar managerii au nevoie de metode
speciale de analiza.
Cateva
din intrebarile la care vom incerca sa raspundem in continuare
sunt:
Care este termenul de terminare al
proiectului?
Care sunt momentele de inceput
si de terminare ale fiecarei activitati?
Care activitati sunt
critice, in sensul ca ele trebuie sa se termine exact in termenul
planificat, astfel incat sa nu fie depasit termenul final de
realizare al proiectului?
Cat de mult pot fi intarziate
activitatile necritice astfel incat sa nu fie depasit
termenul final de realizare al proiectului?
Cum pot fi alocate resursele
diverselor activitati astfel incat proiectul sa se realizeze
rapid si cu costuri minime?
Metodele PERT si CPM,
acronimele pentru Program Evaluation Review Technique si Critical Path
Method, graficele Gant, sunt metode de analiza utilizate pentru
managemenul proiectelor. Indiferent de metoda primul pas in planificarea
proiectelor este definirea activitatilor si stabilirea
relatilor de precedenta dintre acestea. Aceasta este partea cea
mai importanta a unui proiect si in mod normal in aceasta
etapa ar trebui implicate mai multe persoane, astfel incat sa nu fie
uitata nici o activitate importanta.
Exemplu
In prezent
firma ABC are birouri doar in Bucuresti, si doreste sa
deschida birouri noi in Brasov. In acest scop
o parte din personalul din Bucuresti se va muta in Brasov si se va angaja personal
nou. In timp ce economistii trebuie sa se ocupe de partea
financiara a afacerii, arhitectii trebuie sa se ocupe de
proiectarea interioarelor.
Anumite
parti ale proiectului nu pot incepe pana cand altele nu sunt
terminate. De exemplu, nu pot fi amenajate birourile daca acestea nu au
fost inca proiectate, sau nu se poate angaja personal pana nu se stabileste personalul necesar. In
tabelul II.4.1 sunt prezentate activitatile din care este
alcatuit proiectul.
|
Activitatea
|
Descriere
|
Activitati precedente
|
Durata de realizare
(saptamani)
|
|
A
|
Selectarea birourilor
|
-
|
3
|
|
B
|
Stabilirea planului de organizare si a celui
financiar
|
-
|
5
|
|
C
|
Determinarea personalului necesar
|
B
|
3
|
|
D
|
Proiectarea interioarelor
|
A, C
|
4
|
|
E
|
Amenajarea birourilor
|
D
|
8
|
|
F
|
Selectarea personalului care se va muta
|
C
|
2
|
|
G
|
Angajarea de personal nou
|
F
|
4
|
|
H
|
Mutarea propriu-zisa
|
F
|
2
|
|
I
|
Stabilirea relatiilor cu noii parteneri din Brasov
|
B
|
5
|
|
J
|
Instruirea peronalului
|
H, E, G
|
3
|
Tabelul II.4.1 - Activitatile proiectului
Fiecare activitate este plasata intr-un rand separat,
iar in coloana Activitati precedente sunt trecute
activitatile care trebuie realizate inaintea inceperii activitatii analizate. De
exemplu activitatea C nu poate incepe pana nu se termina activitatea
B. In coloana Durata de realizare este trecut timpul estimat pentru realizarea
activitatilor.
Grafice Gant
Una din
metodele cele mai populare folosite pentru planificarea proiectelor este utilizarea graficelor Gant.
Fiecare activitate este desfasurata pe axa verticala. Pe
axa orizontala este reprezentat timpul. Activitatile sunt
reprezentate prin bare de lungime egala cu timpul de realizare a
activitatii. Graficul indica si termenul cel mai devreme de
incepere a fiecarei activitati. De exemplu, activitatea C nu
poate incepe inainte de sfarsitul saptamanii 5, deoarece
activitatea B trebuie sa se termine inainte ca C sa inceapa. Pe masura
ce o activitate este realizata bara asociata este hasurata.
Astfel, in orice moment de timp este foarte clar ce activitati au
fost realizate la timp si care nu. Graficul din figura II.4.1 arata
ca in saptamana 13 activitatile D, E si H sunt in
urma planului, iar activitatea G este inaintea planului.
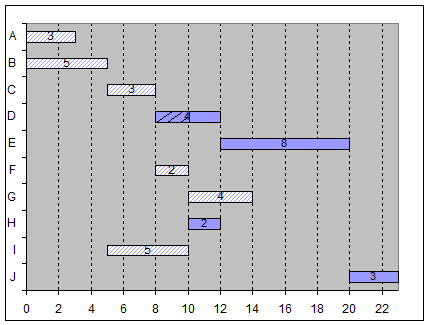
Figura II.4.1 - Graficul Gant
In contextul graficelor Gant "in plan" inseamna ca activitatea nu a fost
finalizata mai tarziu de cel mai devreme termen de terminare a
activitatii. Astfel, in figura II.4.1 putem observa ca
activitatile D si H ar trebui sa se termine cel mai devreme
in saptamana 12. Deoarece nu sunt terminate in saptamana 13
ele sunt in urma planului.
Din graficele Gant nu se pot stabili predecesorii
imediati ai unei activitati. In figura II.4.1 poate parea
ca F si I sunt
activitati precedente ale activitatii G, deoarece G poate incepe
in saptamana 10, iar F si I se pot termina atunci. Dar din
tabelul II.4.1 stim ca doar F este "predecesor imediat" a lui G. O
intarziere a activitatii I nu ar afecta momentul de incepere al
activitatii G. Astfel de informatii sunt importante pentru
manager pentru ca ar putea sa stabileasca ce activitati
ar putea fi intarziate fara a modifica termenul final de realizare al
proiectului. Graficele Gant nu pot fi folosite pentru astfel de analize, in
acest caz fiind recomandata metoda de reprezentare a proiectului printr-un
graf.
Reprezentarea proiectelor prin
grafuri
Fiecare
activitate este reprezentata in graf printr-un arc. Inceputul si
sfarsitul fiecarei activitati sunt indicate printr-un cerc
numit nod. Fiecarui nod i se atribuie un numar. Modul de
atribuire a numerelor este arbitrar. Pe masura ce se
construieste graful nodurile se pot renumerota, dar trebuie pastrate
corect relatiile de precedenta intre activitati.
Fiecare activitate trebuie sa inceapa in nodul in care activitatea
precedenta se termina. De exemplu, in figura II.4.2, activitatea C
incepe in nodul 3, deoarece activitatea precedenta B se termina aici.
Figura II.4.1 - Graful pentru activitatile de la A
la C
Figura II.4.2 - Graful partial
Complicatii
apar in momentul in care incercam sa adaugam activitatea D
in graf. Si A si C sunt
activitati precedente pentru D, si cum vrem ca in graf
activitatea D sa apara o singura data trebuie sa
combinam nodurile 2 si 4 din figura II.4.2 intr-unul singur. Acest
lucru este aratat in figura II.4.3. Nodul 2 (au fost renumerotate
nodurile) reprezinta evenimentul in care activitatile A si
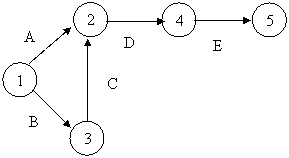
C au fost terminate. Activitatea E, care are ca activitate precedenta doar
pe D poate fi adaugata fara dificultate. Cand incercam
sa adaugam activitatea F apar din nou probleme. Cum F are
activitate precedenta pe C, ar trebui ca activitatea F sa inceapa
in nodul 3. Dar acest lucru ar insemna ca activitatea F are ca activitate
precedenta si pe A, ceea ce este incorect.
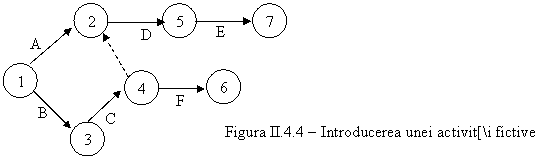
Aceasta dilema poate
fi rezolvata prin introducerea unei activitati fictive,
reprezenta prin linie punctata in figura II.4.4. Aceasta
activitate nu necesita nici timp si nici resurse.
Astfel,
figura II.4.4 arata ca activitatea D poate incepe dupa ce
si A si C s-au terminat. Similar, F poate incepe dupa ce
activitatea C s-a terminat.
Putem
generaliza modul in care introducem o activitate fictiva in modul
urmator: Presupunem ca vrem sa adaugam o activitate A,
in nodul de start N, dar nu toate activitatile care se termina
in nodul N sunt activitati precedente ale acestei activitati.
Pentru aceasta se creeaza un nou nod M, cu o activitate fictiva de la
nodul M la nodul N. Toate activitatile care se termina in N
si sunt predecesoare ale activitatii A se vor termina in nodul
M. Acum activitatea A poate incepe in nodul M.
Figura
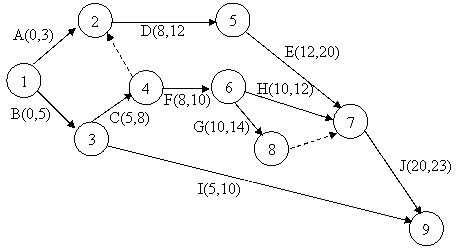
II.4.5 prezinta graful asociat tabelului II.4.1.
Figura II.4.5 - Graful de retea
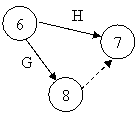
Fiecare activitate este
identificata printr-un nod de start si unul de terminare. In graful
din figura II.4.5 s-ar putea face confuzia ca G si H reprezinta
aceeasi activitate. Pentru a evita confuzia se introduce o noua
activitate fictiva (figura II.4.6).
Figura II.4.6 - Introducerea celei de a doua
activitati fictive
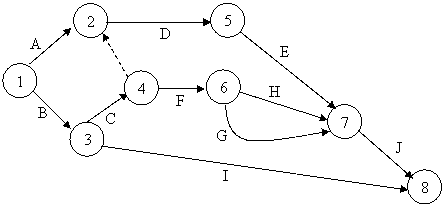
Astfel,
graful final are forma din figura II.4.7.
Figura II.4.7 - Graful final
Din tabelul
4.1. se poate calcula (adunand duratele de realizare ale
activitatilor) ca timpul total de realizare al proiectului este
de 39 de saptamani. Termenul acesta poate fi mai mic deoarece unele
activitati se pot desfasura simultan (de exemplu
activitatile A si B).
Pentru a
afla termenul minim de realizare al proiectului trebuie sa calculam drumul
critic. Un drum intr-un graf este o succesiune de activitati de
la nodul initial (1) la nodul final (9). De exemplu secventa B-I
necesita 10 saptamani pentru a fi realizata secventa
B-C-D-E-J 23 de saptamani. Intr-un graf pot fi identificate mai multe
drumuri de la nodul initial la cel final, cu durate diferite. Se pune
problema determinarii celui mai lung drum de la nodul initial la cel
final. Acest drum, numit drum critic, va determina timpul de realizare al
proiectului, deoarece nici un alt drum nu este mai lung. Daca
activitatile de pe drumul critic sunt intarziate, intregul proiect va
fi intarziat. Din aceasta cauza activitatile care se
gasesc pe drumul critic se numesc activitati critice.
Activitatile critice trebuie realizate "la termen".
Problema se
rezolva in modul urmator:
Se calculeaza pentru fiecare activitate cel mai devreme
termen de incepere si cel mai devreme termen de terminare.
Vom nota cu:
DI - cel mai devreme termen pentru inceperea unei
activitati
DT - cel mai devreme termen pentru terminarea unei
activitati
t - durata estimata a activitatii.
Pentru o activitate, relatia dintre aceste marimi
este: DT=DI+t
Termenul DI pentru o activitate care pleaca dintr-un
nod este cel mai mare DT al activitatilor care se termina in acel nod.
Pentru fiecare activitate din retea se calculeaza DI si DT.
Rezultatul este prezentat in figura II.4.8.
Figura II.4.8 - Termenele DI si DT
Deci, cel mai devreme termen de terminare al proiectului
este de 23 de saptamani.
Se calculeaza cel mai tarziu termen de incepere si
terminare a activitatii. Pentru a identifica activitatile
critice si intervalele de timp cu care activitatile necritice
pot fi intarziate fara a afecta termenul de finalizare al proiectului,
se parcurge graful inapoi de la nodul final la nodul initial. Ideea este
ca odata ce se cunoaste termenul de realizare al proiectului (23
de saptamani), pornind de la aceasta valoare putem calcula cel
mai tarziu termen la care se poate termina o activitate fara a
intarzia intregul proiect. Evaluarea incepe de la nodul final spre nodul
initial.
Vom nota cu:
TI - cel mai tarziu termen de incepere a unei
activitati
TT - cel mai tarziu termen de terminare a unei
activitati
Relatia dintre aceste marimi este: TI = TT - t
Termenul TT pentru o activitate care se termina intr-un
nod este cel mai mic TI al
activitatilor care pleaca din acel nod.
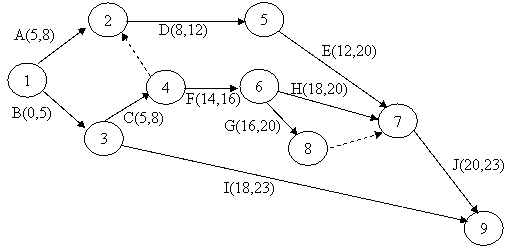
Rezultatele sunt prezentate in figura II.4.9.
Figura II.4.9 - Calcularea TI si TT
Determinarea rezervei de timp asociate fiecarei
activitati.
Rezerva de timp este timpul cu care o activitate
poate fi intarziata fara a afecta termenul de finalizare al
proiectului. Rezerva de timp (RT) se calculeaza cu formula: RT = TI - DI =
TT - DT
De exemplu, pentru activitatea G, rezerva de timp este:
RTG = TIG - DIG = 16 - 10 =
6 sau
RTG = TTG - DTG = 20 - 14 =
6
Aceasta
inseamna ca activitatea G poate intarzia cu 6 saptamani
dupa cel mai devreme termen de incepere a activitatii fara a intarzia proiectul.
Pentru activitatea C:
RTC = TIC - DIC =5 - 5 = 0
Deci activitatea C nu are rezerva de timp si
trebuie sa inceapa in saptamana 5. Cum aceasta
activitate nu poate fi intarziata fara a afecta intregul
proiect, inseamna ca aceasta activitate este o activitate critica.
Activitatile
care au rezerva de timp 0 sunt activitati critice.
Rezolvarea cu Excel
Rezolvarea
problemelor de managementul proiectelor cu Excel se face folosind abordarea
bazata pe grafuri. Foaia de calcul care contine acest model este
prezentata in figura II.4.10.
Datele
si formulele introduse sunt cele rezultate prin dezvoltarea grafului
atasat proiectului. De exemplu, deoarece cel mai tarziu termen de
terminare a activitatii F este cea mai mica valoare dintre cele
mai tarzii termene de incepere ale activitatilor G, F si K,
formula din celula G7 va fi = MIN(F8, F9, F12). Deoarece cel mai devreme termen
pentru inceperea activitatii D
este cea mai mare valoare din cele mai devreme termene de terminare ale
activitatilor A si C,
formula din D5 este = MAX(E2,E4). In
coloana activitate critica este trecut cuvantul DA pentru
activitatile care au abaterea 0.
Figura II.4.10 - Foaia de calcul Excel
Formulele utilizate in foaia de calcul sunt:
|
Celula
|
Formula
|
Se copieaza in
|
|
D4
|
=MAX(E3)
|
-
|
|
D5
|
=MAX(E2,E4)
|
-
|
|
D6
|
=MAX(E5)
|
-
|
|
D7
|
=MAX(E4)
|
-
|
|
D8
|
=MAX(E7)
|
-
|
|
D9
|
=MAX(E7)
|
-
|
|
D10
|
=MAX(E3)
|
-
|
|
D11
|
=MAX(E6,E8,E9)
|
-
|
|
E2
|
=D2+C2
|
E3:E11
|
|
F2
|
=G2-C2
|
F3:F11
|
|
G2
|
=MIN(F5)
|
-
|
|
G3
|
=MIN(F4,F10)
|
-
|
|
G4
|
=MIN(F5,F7)
|
-
|
|
G5
|
=MIN(F6)
|
-
|
|
G6
|
=MIN(F11)
|
-
|
|
G7
|
=MIN(F8,F9)
|
-
|
|
G8
|
=MIN(F11)
|
-
|
|
G9
|
=MIN(F11)
|
-
|
|
G10
|
=E13
|
-
|
|
G11
|
=E13
|
-
|
|
H2
|
=F2-D2
|
H3:H11
|
|
I2
|
=IF(H2=0,"DA","NU")
|
I3:I1
|
|
E13
|
=MAX(E2:E11)
|
-
|
Reprezentarea grafica a
graficelor Gant in Excel
In graficul
Gant activitatile sunt afisate pe axa verticala iar pe axa
orizontala este reprezentat timpul. Graficul indica cel mai devreme
termen de incepere a fiecarei activitati si durata
activitatii. Vom ilustra modul de construire a graficelor Gant pentru
exemplul din figura II.4.10.
Se selecteaza datele care vor fi reprezentate in
grafic: activitatile (A1:A11), durata activitatilor
(C1:C11) si cel mai devreme termen de incepere a activitatilor
(D1:D11).
Se creeaza un grafic de tip Staked Bar.
Se selecteaza seria DI. Se apasa butonul din
dreapta al mouse-ului si se selecteaza comanda Format Series.
Se selecteaza butonul Series Order si se stabileste
pentru afisarea seriilor ordinea DI, Durata. Se selecteaza butonul Patterns,
si in sectiunile Border si Area se selecteaza
optiunile None. Deci barele atasate termenelor de incepere ale
activitatilor vor fi transparente, iar barele care reprezinta
durata activitatilor vor aparea in prelungirea lor.
Se selecteaza seria Durata, se apasa butonul din
dreapta al mouse-ului si se selecteaza comanda Format Series.
Se selecteaza butonul Data Labels, optiunea Show Value.
Astfel in dretul fiecarei bare va fi afisata durata activitatii.
Se selecteaza axa Y, se apasa butonul din dreapta
al mouse-ului si se selecteaza comanda Format Axis. Se
selecteaza butonul Scale, optiunile Categories in reverse
order si Value (Y) axis crosses at maximum category. Astfel
activitatile vor fi afisate incepand din partea de sus a axei y.
Modelul de analiza a drumului
critic/cost
Pentru
reducerea timpului de realizare a unui proiect, analistul poate incerca
reducerea duratei in care se efectueaza anumite activitati de pe
drumul critic prin alocarea de resurse suplimentare. De exemplu, o activitate
care dureaza in mod normal 2 saptamani daca se
lucreaza 8 ore pe zi, poate fi terminata mai repede daca se
lucreaza peste program sau daca se mareste numarul de
muncitori. Acest lucru, bineinteles, se realizeaza cu pretul
unor costuri crescute. Problema care se pune este: "Ce activitati ar
trebui urgentate astfel incat reducerea termenului final de realizare al
proiectului sa se faca cu costuri minime?".
Acest model presupune ca
costul este o functie liniara de timp, descrescatoare, deoarece
orice efort de urgentare este insotit de cresterea cheltuielilor
(figura II.4.11).
Figura II.4.11 - Functia cost - durata
Pentru
fiecare activitate se cunosc urmatoarele date:
Timpul
normal - timpul maxim de realizare a activitatii
Costul
normal - costul
necesar pentru realizarea activitatii in timpul normal de lucru
Timpul
minim - timpul minim in care se poate realiza activitatea
Cost maxim - costul
necesar pentru realizarea lucrarii in timpul minim
Pentru
prezentarea metodei vom folosi urmatorul exemplu:
Un proiect,
cu graful asociat prezentat in figura II.4.13, este alcatuit din 5
activitati. Pentru fiecare activitate se cunosc timpul normal, timpul
minim, costul normal si costul maxim (prezentate in tabelul II.4.2).
|
Activitate
|
Timp normal (ore)
|
Cost normal ($)
|
Timp minim (ore)
|
Cost maxim ($)
|
Costul urgentarii/ora
|
|
A
|
32
|
640
|
20
|
800
|
13.3
|
|
B
|
40
|
480
|
30
|
720
|
24
|
|
C
|
50
|
1000
|
30
|
1200
|
10
|
|
D
|
24
|
288
|
15
|
360
|
8
|
|
E
|
120
|
4800
|
70
|
5600
|
16
|
|
Total
|
|
7208
|
|
|
|
Tabelul II.4.2 - Activitatile proiectului
In ultima coloana din
tabel s-a calculat pentru fiecare activitate costul urgentarii pe ora
egal cu (Costul maxim-Costul normal)/(Timpul normal-Timpul minim) .
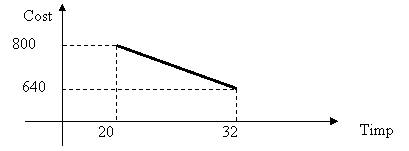
Figura II.4.12 ilustreaza functia cost -
durata pentru activitatea A.
Figura II.4.12 - Functia cost - durata pentru
activitatea A
Graful asociat problemei este prezentat in figura II.4.13.
Figura II.4.13 - Graful asociat problemei
Utilizand
duratele normale pentru fiecare activitate, cel mai devreme termen pentru
finalizarea proiectului este 194 ore (pe drumul critic C-D-E).
Pentru a
reduce termenul de finalizare al proiectului la 193 de ore o activitate de
pe drumul critic trebuie urgentata
cu o ora. Cum costul urgentarii pe ora pentru activitatea D este
mai mic decat costurile urgentarii pe ora pentru
activitatile C si E (8<10 si 8<16), se va urgenta
activitatea D cu o ora. Astfel, proiectul se va termina in 193 de ore,
drumul critic va fi C-D-E si costul total 7208+8=7216.
Daca
termenul de finalizare mai trebuie redus cu o inca ora la 192 ore,
aplicand un rationament asemanator se urgenteaza
activitatea D cu inca o ora si costul marginal va creste cu
8$.
Daca termenul de finalizare trebuie redus mai mult, la
191 ore, problema se complica. Situatia este ilustrata in figura
II.4.4. Acum exista doua drumuri critce A-B-E si C-D-E, ambele
de 192 ore.
Figura II.4.4 - Graful pentru timpul de finalizare de 191
ore
Urgentarea
uneia dintre activitatile A, B, C, D cu o ora va reduce un drum
cu o ora dar drumul critic va ramane tot de 192 ore. Un drum critic
de 191 de ore se poate obtine daca se urgenteaza
activitati de pe ambele drumuri, sau daca se urgenteaza
doar activitatea E. Deci exista mai multe alternative, iar dintre acestea
trebuie gasita solutia care are costul minim. Pentru grafuri
complexe rezolvarea in acest mod ar fi foarte greoaie. Problema poate fi
rezolvata simplu cu ajutorul programarii liniare. Figura II.4.5
contine modelul atasat problemei.
Figura II.4.5 - Foaia de calcul utilizata pentru rezolvarea
problemei
Formulele utilizate in foaia de calcul sunt:
|
Celula
|
Formula
|
Se copieaza in
|
|
F2
|
=B2-D2
|
F3:F6
|
|
G2
|
=(E2-C2)/(B2-D2)
|
G3:G6
|
|
D9
|
0
|
-
|
|
D10
|
=E9
|
-
|
|
D11
|
0
|
-
|
|
D12
|
=E11
|
-
|
|
D13
|
=MAX(E10,E12)
|
-
|
|
E9
|
=D9+C9
|
E10:E13
|
|
F9
|
=G9-C9
|
F10:F13
|
|
G9
|
=F10
|
-
|
|
G10
|
=F13
|
-
|
|
G11
|
=F12
|
-
|
|
G1
|
=F13
|
-
|
|
G13
|
=E13
|
-
|
|
H9
|
=F9-D9
|
H10:H13
|
|
I9
|
=IF(H9=0,"***","")
|
I10:I13
|
|
D14
|
=E13
|
-
|
|
C15
|
=SUMPRODUCT(B9,B13,G2:G6)
|
-
|
In prima
parte a foii de calcul se introduc timpul normal, costul normal, timpul minim
si costul maxim de realizare a fiecarei ativitati. Pe baza
acestor date, se calculeaza in coloana Durata maxima a
urgentarii durata maxima cu care poate fi urgentata fiecare
activitate (diferenta dintre timpul normal si timpul minim), iar in
coloana urmatoare costul urgentarii pe ora (diferenta
dintre costul maxim si costul normal raportata la durata maxima
a urgentarii).
Al doilea
tabel din foaia de calcul contine variabilele de decizie ale problemei -
duratele cu care poate fi urgentata fiecare activitate (in domeniul
B9:B13). Initial toate valorile vor avea valoarea 0.
In coloana
Durata activitatii se calculeaza durata activitatii in
cazul in care aceasta va fi urgentata cu valoarea din coloana Durata
urgentarii (diferenta dintre durata normala si durata
urgentarii).
In coloanele
urmatoare se calculeaza cele mai devreme si cele mai tarzii
termene de incepere si terminare al fiecarei activitati,
respectand succesiunea activitatilor (la fel ca in exemplul
anterior). Apoi, se calculeaza pentru fiecare activitate abaterile si
se introduc formulele pentru determinarea activitatilor critice.
Functia
obiectiv (celula C15) este minimizarea costului total de urgentare, calculat ca
suma produselor dintre duratele cu care se urgenteaza fiecare activitate
si costul urgentarii activitatii pe unitatea de timp - min(C15).
Restrictiile
problemei sunt:
Durata in care trebuie realizat proiectul
(continuta in celula D14). De exemplu daca proiectul ar trebui
terminat in 184 de ore, restrictia ar fi D14=184
Durata cu care poate fi urgentata fiecare activitate nu
poate depasi durata maxima de urgentare, iar aceste durate sunt
numere pozitive. Deci,
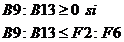
Se
rezolva problema cu ajutorul Solver-ului, iar rezultatele
obtinute arata ca pentru ca proiectul sa se termine cu
costuri minime in 184 de ore, trebuie urgentate lucrarile D cu 2 ore
si E cu 8 ore. Costul suplimentar al urgentarii ar fi in acest caz de
144$.