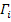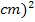Determinarea coordonatelor unui punct prin metoda intersectiei
multiple inapoi
Metoda intersectiei inapoi
reprezinta o metoda topo-geodezica utilizata in vederea
indesirii retelei de sprijin necesara executarii
ridicarilor topografice de detaliu.
Pozitia unui punct in plan se poate determina prin intersectie
inapoi daca se cunosc unghiurile formate de directiile spre punctele vechi
si coordonatele acestora.Asadar, pe teren se stationeaza
doar in punctual nou si se masoara unghiurile formate de directiile
spre cel putin patru puncte cunoscute din reteaua geodezica de
sprijin.
Metoda este avantajosa sub raportul
lucrarilor de teren dar calulele au constituit in teren o
problema.Din acest motiv in rezolvarea interesectiei inapoi
-cunoscuta in literatura sub numele de Pothénot sau
retrointersectie- s-au cautat mereu solutii si se cunosc
doua rezolvari si anume Procedeul Delamber si Procedeul
Collins.
Coordonatele rectangulare ale punctului de
retrointersectie se pot determina semiriguros prin metode analitice de
calcul sau riguros prin metoda celor mai mici patrate.
Lipsa vizibilitatii catre orice
punct din reteaua de sprijin de pe suprafata de lucru din tema de
proiect a impus alegerea amplasamentului unui punct din imediata vecinatate a corpului
de proprietate,astfel incat sq fie vizibilitate catre cat mai multe
puncte.
Alegerea amplasamentului punctului de lucru
din retrointersectie s-a facut astfel incat sa se poata efectua
masuratori unghiulare in conditii optime de lucru si de
semenea sa poata fi asigurata transmiterea coordonatelor acestui
punct de pe suprafata corpului de proprietate.
Dupa materializarea punctului de
retrointersectie s-au efectuat masuratori unghiulare catre cinci
puncte din reteaua geodezica si anume:punctele
1002,1004,1007,1010,1012.
In tabelul 2.1 sunt inregistrate
directiile azimutale din punctul nou si coordonatele rectangulare ale
punctelor retelei geodezice.
Determinarea coordonatelor punctui de
intersectie notat cu 2007 s-a facut prin metode riguroase,metoda
retrointersectiei facandu-se un numar de patru
combinatii.In continuare se face prezentarea modelului de lucru.
Pentru inceput se prezinta datele
necesare procesului de lucru:
1.Schita cu punctele retelei de
triangulatie(figura 2.1);
2.Coordonatele rectangulare absolute ale
punctelor vechi din reteaua de triangulatie(tabelul 1.1)
3. Valorile numerice ale
masuratorilor unghiulare(tabelul 1.1)
Date
cunoscute:
Tabel 1.1
|
Punct statie
|
Nr. Punct vizat
|
Directii
orizontale
|
Coordonate
rectangulare plane
|
|
X
|
Y
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.1 Calculul
coordonatelor provizorii ale punctului nou
Observatiile geodezice efectuate pe
suprafata terestra (reala) sunt raportate la verticala locului,
in functie de care se orienteaza axa principala (verticala)
a instrumentului si care este perpendiculara pe suprafata de
nivel ce trece prin punctul de statie. Deoarece prin calcul, determinarea
punctului se face fata de alte suprafete de referinta
(elipsoidul de referinta, sfera de raza medie sau planul de
proiectie) pozitia verticala trebuie raportata la normalele
duse la aceste suprafete, rezultand diverse unghiuri de deviatie a
verticalei, asa cum s-a prezentat la cursurile de Cartografie matematica
si de Geodezie elipsoidala. In retelele de triangulatie de
indesire, ca in cazul de fata, calculele se executa in raport cu o
suprafata plana, corespunzatoare proiectiei "stereo
"70". Din aceasta cauza, inainte de a fi folosite in compensarea
riguroasa, observatiile azimutale efectuate pe teren, prin metoda
seriilor complete, se compenseaza in statie, dupa care se reduc mai
intai la elipsoidul de referinta prin aplicarea a trei corectii
(corectia de linie geodezica, corectia datorata altitudinii
punctului vizat si corectia datorata deviatiei verticalei), la
care se adauga corectiile de centrare si de reducere. Pentru
prelucrarea directiilor azimutale in planul de proiectie se aplica
si corectiile de reducere la coarda. Pentru calculul acestor
corectii este necesar calculul coordonatelor preliminare ale tuturor
punctelor noi.
Coordonatele preliminare se determina
prin intersectii inainte sau inapoi, utilizand directiile medii
masurate si coordonatele punctelor vechi.
Calculul coordonatelor provizorii ale
punctului nou se face prin intersectie inapoi Procedeul Collins, din mai
multe puncte vechi (unele din aceste vize sunt catre turle de biserici,
care sunt insa deosebit de utile deoarece sunt usor vizibile , chiar
de la distante mari) din reteaua de triangulatie, se
efectueaza observatii azimutale.
In vederea determinarii coordonatelor
rectangulare plane X,Y ale punctului 2007 s-a folosit ca procedeu de lucru
metoda retrointersectiei facandu-se un numar de patru
combinatii.
Varianta I : 1002-1010-1012
Inventarul de coordonate
al punctelor de sprijin
Tabel 1.2
|
Nr. pct.
|
Nume
punct
|
Coordonate
rectangulare plane
|
|
X(m)
|
Y(m)
|
|
|
|
|
|
|
|
|
|
|
|
|
Schita din teren

Figura:1.2
Schita variantei I 1002-1010-1012
3.Elementele
masurate pe teren
Tabel 1.3
|
Unghi
|
Valoare
numerica
(goni)
|
|
|
|
|
Calculul va cuprinde
urmatoarele etape:
Calculul distanelor orizontale intre punctele
vechi si al orientarilor
directiilor dintre punctele vechi;

Calculul unghiului
 ;
;

Calculul constantei unghiulare A;

Calculul unghiului
 ;
;

Calculul valorilor (A-
 ) si al
unghiurilor
) si al
unghiurilor
 si
si
 ;
;

Calculul orientarilor de la punctele 1002,1010,1012 catre punctul 2007;

Calculul distantelor de la punctele 1002,1010,1012 catre punctul 2007;

Calculul coordonatelor relative ale punctului
nou in raport cu punctele vechi;

Calculul coordonatelor rectangular ale punctului
nou;

Varianta II :
1002-1007-1012
Inventarul de coordonate
al punctelor de sprijin
Tabel 1.4
|
Nr. pct.
|
Nume
punct
|
Coordonate
rectangulare plane
|
|
X(m)
|
Y(m)
|
|
|
|
|
|
|
|
|
|
|
|
|
Schita din teren

Figura:1.2
Schita variantei II 1002-1007-1012
3.Elementele
masurate pe teren
Tabel 1.5
|
Unghi
|
Valoare
numerica
(goni)
|
|
|
|
|
Calculul va cuprinde
urmatoarele etape:
Calculul distanelor orizontale intre punctele
vechi si al orientarilor
directiilor dintre punctele vechi;

Calculul unghiului
 ;
;

Calculul constantei unghiulare A;

Calculul unghiului
 ;
;

Calculul valorilor (A-
 ) si al
unghiurilor
) si al
unghiurilor
 si
si
 ;
;

Calculul orientarilor de la punctele 1002,1007,1012 catre punctul 2007;

Calculul distantelor de la punctele 1002,1007,1012 catre punctul 2007;

Calculul coordonatelor relative ale punctului
nou in raport cu punctele vechi;

Calculul coordonatelor rectangular ale punctului
nou;

Varianta III :
1004-1010-1012
Inventarul de coordonate
al punctelor de sprijin
Tabel 1.6
|
Nr. pct.
|
Nume
punct
|
Coordonate
rectangulare plane
|
|
X(m)
|
Y(m)
|
|
|
|
|
|
|
|
|
|
|
|
|
Schita din teren

Figura:1.2
Schita variantei III 1004-1010-1012
3.Elementele
masurate pe teren
Tabel
1.7
|
Unghi
|
Valoare
numerica
(goni)
|
|
|
|
|
Calculul va cuprinde
urmatoarele etape:
Calculul distanelor orizontale intre punctele
vechi si al orientarilor
directiilor dintre punctele vechi;

Calculul unghiului
 ;
;

Calculul constantei unghiulare A;

Calculul unghiului
 ;
;

Calculul valorilor (A-
 ) si al
unghiurilor
) si al
unghiurilor
 si
si
 ;
;

Calculul orientarilor de la punctele 1004,1010,1012 catre punctul 2007;

Calculul distantelor de la punctele 1004,1010,1012 catre punctul 2007;

Calculul coordonatelor relative ale punctului
nou in raport cu punctele vechi;

Calculul coordonatelor rectangular ale punctului
nou;

Varianta IV :
1007-1010-1012
Inventarul de coordonate
al punctelor de sprijin
Tabel 1.8
|
Nr. pct.
|
Nume
punct
|
Coordonate
rectangulare plane
|
|
X(m)
|
Y(m)
|
|
|
|
|
|
|
|
|
|
|
|
|
Schita din teren

Figura:1.2
Schita variantei IV1007-1010-1012
3.Elementele
masurate pe teren
Tabel 1.9
|
Unghi
|
Valoare
numerica
(goni)
|
|
|
|
|
Calculul va cuprinde
urmatoarele etape:
Calculul distanelor orizontale intre punctele
vechi si al orientarilor
directiilor dintre punctele vechi;

Calculul unghiului
 ;
;

Calculul constantei unghiulare A;

Calculul unghiului
 ;
;

Calculul valorilor (A-
 ) si al
unghiurilor
) si al
unghiurilor
 si
si
 ;
;

Calculul orientarilor de la punctele 1007,1010,1012 catre punctul 2007;

Calculul distantelor de la punctele 1007,1010,1012 catre punctul 2007;

Calculul coordonatelor relative ale punctului
nou in raport cu punctele vechi;

Calculul coordonatelor rectangular ale punctului
nou;

Calculul preciziei de determinare ale
coordonatelor punctului nou 2007;




|
Pct.
|
Coord. rectangulare
plane
|
Abateri pe
abscisa
|
Abateri pe
ordonata
|
Raza de
indecizie
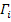
|
|
X
(m)
|
Y
(m)
|
dx
(cm)
|

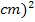
|
dy
(cm)
|

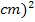
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
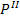
|
|
|
|
|
|
|
|
|
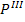
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|

|
|
|
Raza medie de indecizie =0.0016
|
2.2 Compensarea coordonatelor punctului 2700, determinat
prin intersectie multipla inapoi.
Datele
initiale:
Schita cu punctele retelei
de triangulatie si vizele azimutale ;
Coordonatele rectangulare plane ale
punctelor vechi (cunoscute) ale
retelei geodezice de triangulatie - tabelul 1.11;
Directiile azimutale
masurate in retea, centrate si reduse in planul de
proiectie - tabelul 1.11.
Tabel 1.11
|
Punct statie
|
Nr. Punct vizat
|
Directii
reduse
|
Coordonate
rectangulare plane
|
|
X
|
Y
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Succesiunea operatiilor de calcul este urmatoarea:
Calculul
coordonatelor provizorii ale punctului nou;
Calculul
orientarilor si distantelor provizorii dintre punctul nou si
cele vechi;
Calculul coeficientilor
de directie si verificarea lor
Calculul termenilor liberi
Scrierea
sistemului initial al ecuatiilor de corectii
Scrierea sistemului final al ecuatiilor de
corectii
Intocmirea sistemului
ecuatiilor normale al necunoscutelor
Rezolvarea
sistemului ecuatiilor normale si verificarea solutiilor
Calculul
coordonatelor compensate ale punctului nou
Calculul corectiei unghiului de orientare al
statiei si a valorii compensate a unghiului
Calculul
corectiilor si a sumei patratelor corectiilor
Calculul valorilor compensate ale directiilor azimutale si ale orientarilor
directiilor, inclusiv controlul compensarii
Calculul erorii medii patratice a unei singure masuratori directe
Calculul erorilor medii patratice ale
marimilor compensate ale necunoscutelor si erorii totale in pozitia punctului pe plan
Calculul elementelor elipsei erorilor si ale
podarei elipsei erorilor pentru punctul
nou
Constructia grafica a podarei elipsei erorilor la scara 3:1
Calculul erorilor medii patratice ale
marimilor compensate ale orientarilor si
distantelor dintre punctul nou si punctele vechi.
S-au folosit urmatoarele notatii:
r - numarul de directii masurate;
n - numarul de necunoscute;
i - punct vechi de coordonate cunoscute;
 ,
,
 - coordonatele rectangulare ale punctelor vechi;
- coordonatele rectangulare ale punctelor vechi;
 ,
,
 - coordonatele
rectangulare compensate ale punctului nou;
- coordonatele
rectangulare compensate ale punctului nou;
 ,
,
 - coordonatele
provizorii ale punctulului nou;
- coordonatele
provizorii ale punctulului nou;
Dxo, Dyo - coordonate relative provizorii;
 - distante provizorii;
- distante provizorii;
q
 orientarea provizorie a fiecarei
directii masurate;
orientarea provizorie a fiecarei
directii masurate;
Zio - unghi de orientare individual pe fiecare
directie masurata;
a
 - directie azimutala provizorie
centrata si redusa la plan;
- directie azimutala provizorie
centrata si redusa la plan;
Z
 - unghi mediu de orientare provizoriu;
- unghi mediu de orientare provizoriu;
li - termenul liber pentru directia
masurata din statia i
ai, bi - coeficientii de
directie;
dx, dy, dz - necunoscute;
vi - corectii rezultate din
compensare;
Z2007 - unghi mediu de orientare compensat;
a2007-i -
directie azimutala compensata;
q2007-i -
orientarea compensata a fiecarei directii masurate
Calculul
va cuprinde urmatoarele etape:
Calculul coordonatelor
provizorii ale punctului nou.
Pentru compensarea
riguroasa, indiferent de metoda de compensare folosita (metoda
observatiilor indirecte sau conditionate) sunt necesare coordonatele
provizorii ale punctelor noi ale retelei geodezice de triangulatie.
Avand coordonatele
punctelor vechi si directiile azimutale centrate si reduse la
planul de proiectie, se calculeaza pentru punctele noi, o noua
serie de coordonate, denumite coordonate
provizorii, aproximarea de calcul a acestora fiind
imbunatatita in raport cu coordonatele preliminare.
S-a efectuat calculul coordonatelor provizorii
ale punctului nou 2007 prin intersectie
multipla
inapoi folosind metoda variatiei coordonatelor.

Calculul
orientarilor si distantelor provizorii dintre punctul nou si
cele vechi.
Pe baza coordonatelor
cunoscute ale punctelor vechi Xi ,Yi , i=
 (tabelul 1.11)
si ale coordonatelor provizorii ale punctului nou 2007, se calculeaza
mai intai orientarile provizorii ale directiilor, folosind
relatia
(tabelul 1.11)
si ale coordonatelor provizorii ale punctului nou 2007, se calculeaza
mai intai orientarile provizorii ale directiilor, folosind
relatia
 =
=

unde i - punctul vechi .
Distantele
provizorii se calculeaza cu formulele :
 =
=
 =
=

Operatiile de calcul se conduc in tabelul 1.12, coloanele 1-6.
Tabel 1.12
|
Nr
pct
|
Coordonate absolute
|

|

|

|
a
|
Control

| |
|

(m)
|

(m)
| |
|

|

|
b
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
Calculul
coeficientilor de directie si verificarea lor
Coeficientii de directie reprezinta coeficientii
necunoscutelor din ecuatiile de corectii si exprima
variatia orientarii pe unitatea de lungime considerata
(coeficientul a pe axa X si coeficientul b pe axa Y). Din motive practice,
in triangulatia de stat corectiile unghiulare se exprima in
secunde, iar necunoscutele (corectiile coordonatelor), in decimetri. De
asemenea, distantele intre puncte, ca si coordonatele relative, se
exprima in kilometri.Din aceasta cauza, formulele folosite in
practica calcularii coeficientilor de directie pentru cazul gradatiei centezimale sunt :


Pe baza acestor
formule se calculeaza coeficientii de directie a2007-i si
b2007-i (2007 - punct nou, i - punct vechi), in acelasi tabel
cu calculul orientarilor si distantelor provizorii, coloana 7.
Controlul calcularii coeficientilor de
directie se face cu formula :
a/b = - tg θo, in coloana 8 a
tabelului 1.12.
Calculul termenilor
liberi
Unghiul de orientare al statiei
Z2007 , este unghiul facut de directia nordului cu
directia de referinta in raport cu care s-au masurat pe teren
valorile unghiulare ale directiilor orizontale.(Figura 1.6).

Modificat!!!

Figura 1.6
Marimea acestui unghi se obtine pe baza valorilor unghiulare al
directiilor θ
 , trecute in tabelul 1.13, coloanele 3 si 4, cu
formula:
, trecute in tabelul 1.13, coloanele 3 si 4, cu
formula:
Zi2007=
θo2007-i - αo2007-i
unde: Zi2007 - unghi de orientare
individual pe fiecare directie masurata;
θo2007-i
- orientarea provizorie a
fiecarei directii masurate;
αo2007-i
- directie azimutala provizorie centrata si redusa la
plan;
i - punct
vizat.
Din cauza erorilor de masurare a directiilor orizontale , precum
si a erorilor coordonatelor punctelor vechi, unghiurile de orientare in
statie nu vor fi egale intre ele,decat in mod intamplator. Pentru a
orienta statia se calculeaza un unghi de orientare mediu, cu formula
:
Zo2007
=

unde:
Zo2007 - unghi mediu de
orientare provizoriu;
r - numarul de directii masurate
din statia 2007.
Termenii liberi ai ecuatiilor
de corectii se calculeaza cu relatia
lcc2007-i = Zi2007-
Zo2007
unde: l2007-i - termenul liber pentru directia
masurata din statia 2007 i;
Zi2007 - unghi de
orientare provizoriu individual pe fiecare directie masurata;
Zo2007- unghi mediu de
orientare provizoriu.
ale caror valori, exprimate in
secunde centezimale, se trec in coloana 6. Se face suma algebrica a
termenilor liberi, verificandu-se conditia [l] = 0.
Tabel
1.13
|
Punct
Statie
|
Punct
vizat
|
Directii centr.
si red. in
pl. Pr.

|
Orientari provizorii

|
Unghi de
orientare statie

|
Termeni
liberi

|
Pond.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z
 =
=
|
|
|
|
Scrierea sistemului initial al ecuatiilor
de corectii
Deoarece pentru fiecare directie azimutala masurata
direct pe teren, va corespunde cate o ecuatie de corectii, pentru
compensarea coordonatelor provizorii ale punctului nou 2007, se va scrie
sistemul initial al ecuatiilor de corectii, de forma
generala:
Ei : -dz + ai dx + bi dy + li
= vi , cu pj =1
unde pentru simplificre, s-au introdus notatiile
a2007-i = ai ; b2007-i = bi; l2007-i = li;
v2007-i = vi ; p2007-i= pj.
Numarul initial al ecuatiilor corectiilor, scrise
pentru directiile masurate, este egal cu numarul directiilor
in cadrul retelei (r = 5).
Scrierea sistemului final al ecuatiilor de
corectii
Deoarece in sistemul
initial al sistemului de corectii necunoscuta dz are
coeficientul egal cu -1, aceasta se va
putea elimina prin aplicarea regulei intai a lui Schreiber sau
situatia 1 de echivalenta. Acest lucru se realizeaza prin introducerea conditiilor [v] = 0 si [l]
= 0.
Sistemul final al ecuatiilor
de corectii se obtine direct din sistemul initial dar
fara necunoscuta dz si avand corectiile vi, la
care se adauga o ecuatie suplimentara, a (r+1)-a. Noul sistem
este ponderat, primele r = 6 ecuatii avand
ponderile egale cu unitatea, iar ultima, a sasea, numita ecuatia
suma, avand ponderea -
 . In acest fel,
sistemul final al ecuatiilor de corectii se va prezenta sub forma
. In acest fel,
sistemul final al ecuatiilor de corectii se va prezenta sub forma
- a1 dx - b1 dy +
l1 = v'1 , cu p1 = 1
- a2 dx - b2 dy + l2
= v'2 , cu p2 = 1
- a3 dx - b3 dy + l3
= v'3 , cu p3 = 1
- a4 dx - b4 dy + l4
= v'4 , cu p4 = 1
- a5 dx - b5 dy + l5
= v'5 , cu p5 = 1
- [a]dx - [b]dy +[l] =
[v'], cu p5 =

Sistemul final al
ecuatiilor de corectii contine un numar de (r+1)=(5+1)=6
ecuatii, cu 7 necunoscute (dx,dy,v1,v2, . ,v4,
v5) astfel ca nu se poate rezolva.
Intocmirea sistemului ecuatiilor normale al necunoscutelor
In sistemul final al ecuatiilor de corectii transformate,
marimile corectiilor v' fiind mici, asemanatoare erorilor,
li se pot aplica principiul de minim :
[pv'v'] → minim
Deoarece suma considerata este o
functie de marimile necunoscutelor ramase dx si dy, prin
anularea derivatei intaia se ajunge la conditiile de minimum
[pav'] = 0 ; [pbv'] = 0 ,
reprezentand lema lui Gauss. Prin inlocuirea corectiilor v' cu expresiile lor din ecuatiile
de corectii finale, se ajunge la un sistem de doua ecuatii cu doua necunoscute, avand
forma:
[paa]dx + [pab]dy + [pal] = 0
[pab]dx + [pbb]dy + [pbl] = 0
si care reprezinta sistemul
ecuatiilor normale al necunoscutelor. In acest sistem, coeficientii
de pe diagonala principala sunt totdeauna patratici iar
coeficientii dreptunghiulari, pozitivi sau negativi, sunt simetrici in
raport cu diagonala principala. In acest caz, determinantul sistemului
este intotdeauna diferit de zero (D ≠ 0), sistemul admitand solutii
unice.
Calculul coeficientilor,
termenilor liberi si termenilor suma ai ecuatiilor normale se
efectueaza in tabelul 1.14.
Pentru controlul
inscrierii corecte ,ca si al calculelor ulterioare, se fac sumele pe
orizontala:
-ai - bi + li
= si , i =

-[a] - [b] +0 = S'
Controlul inscrierii
datelor in tabelul ecuatiilor de corectii finale (ecuatii
fictive echivalente), se face cu ajutorul expresiei evidente
S' = [s], respectiv -2.423= -2.423
Controlul
calcularii coeficientilor, termenilor liberi si ai termenilor
suma, se face cu relatiile

In tabelul 1.15 sunt
trecuti numai coeficientii si termenii liberi ai ecuatiilor
normale scrise sub forma prescurtata. Din aceasta cauza,
incepand cu linia a doua la insumare se vor lua si termenii situati
deasupra termenilor patratici.
Tabel 1.14
|
Nr.
ec.
fictive
|
Pond.
pi
pi+1
|
Coeficienti
|
Termeni liberi
|
Sume
| |
|
-ai
-[a]
|
-bi
-[b]
|
l

[l]
|
si
[s]
| |
|
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
S
|
|
|
|
|
| |
Tabel
1.15
Rezolvarea sistemului ecuatiilor normale
si verificarea solutiilor
Fiind un sistem de
doua ecuatii cu doua necunoscute, rezolvarea lor se face cu
ajutorul metodei Cramer,folosind relatiile
dx
 =0.017 dm= 0.002 m ;
=0.017 dm= 0.002 m ;
dy
 = -0.026 dm= -0.003 m ;
= -0.026 dm= -0.003 m ;
Verificarea
solutiilor se face cu relatia
([pas] - [pal])dx + ([pbs] -
[pbl])dy = -([pls] - [pll])
rezultand:
-0.089= -0.089
Calculul coordonatelor compensate ale punctului nou
Coordonatele rectangulare plane compensate ale punctului nou se obtin
prin insumarea algebrica a coordonatelor provizorii cu marimile
necunoscutelor (corectiilor) :
X = Xo2007 + dx = 5383.213+0.002
=5383.215 m ;
Y = Yo2007 +
dy = 14144.694-0.003 = 14144.6917m;
unde: Xj,
Yj - valorile marimilor coordonatelor compensate;
Xo2007,
Yo2007 - valorile provizorii ale coordonatelor punctelor
noi;
dx, dy - valorile
corectiilor.
Calculul
corectiei unghiului de orientare al statiei si a valorii
compensate a unghiului
Pentru punctul de statie 2007, se
calculeaza necunoscuta dz , reprezentand corectia unghiului de
orientare al statiei :
dz =
 = - 0cc,0030
= - 0cc,0030
unde: [a], [b]
- coeficientii ecuatiilor suma pentru fiecare statie.
Pe baza ei, se calculeaza
unghiul de orientare compensata a directiei de origine :
Z2007 = Zo2007 + dz =
327g 51c 11cc,224 - 0cc,0030/10000
= 327g 51c 11cc,221
Calculul corectiilor si a sumei
patratelor corectiilor
Prin inlocuirea valorilor necunoscutelor dx, dy, dz, in sistemul
initial (netransformat) al ecuatiilor de corectii, se obtin
marimile corectiilor :
Ei : -dz + ai dx + bi
dy - ai dx - bi dy + li = vi (i =
 )
)
Calculul corectiilor se conduce in tabelul 2.16. Se face
verificarea [vj] = 0. In
acelasi tabel se calculeaza suma patratelor corectiilor,
functie directa de marimile acestora, (coloana 8) :
[vv] = v12 + v22
+ . + v52 = 0.069
iar pentru
control, ca suma ale produselor corectiilor cu termenii liberi, (coloana 9)
[vv] = [vl] = v1 l1 + v2 l2+ . +
v4 l4+ v5 l5 = 0.069
Tabel 1.16
|
Nr.ec.
|
Direct.
|
-dzcc
|
-aidx
|
-bidy
|
licc
|
 vi
vi
|
Vivi
|
vili
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
Calculul valorilor compensate ale
directiilor azimutale si ale orientarilor
directiilor, inclusiv controlul compensarii
Pe baza valorilor provizorii ale
directiilor azimutale (centrate si reduse la planul de
proiectie) si ale corectiilor rezultate prin compensare, se
obtin valorile compensate ale directiilor azimutale, folosind
expresia :
α 2007-i= αo2007-i+
vi ; i =

unde: a2007-i - directie azimutala
compensata;
a2007-io - directie
azimutala provizorie centrata si redusa la plan;
vi
- corectii rezultate din compensare.
Cu ajutorul acestora si a unghiului de orientare compensat al
statiei, se calculeaza orientarile compensate ale
directiilor :
Θ2007-i = α2007-i + Z2007-i; i =

unde:
q2007-i - orientarea
compensata a fiecarei directii masurate;
a2007-i - directie
azimutala compensata ;
Z2007-i - unghi mediu de orientare
compensat.
Calculele se conduc in tabelul 1.17.
|
Tabel 1.17
|
|
Directie
|

(g
c cc )
|

(cc)
|

(g c cc )
|
Z100
(g
c cc )
|

(g
c cc )
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pentru controlul final al compensarii se calculeaza
orientarile si distantele dintre punctul nou compensat si
punctele vechi, cu relatiile cunoscute (tabelul 1.18) :
θ
2007-i = arctg

D
 =
=
 =
=
 =
=

|
Tabel 1.18
| |
|
Nr.
Pct.
|
Coordonate absolute
|
tgq/ctgq
|
sinq
|
D = Dx / cosq
D = Dy / sinq
D =

| |
|
Xi/X
(m)
|
Yi/Y
(m)
|
q
( g c cc )
| |
|
cosq
| |
|
|
1
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
Verificarea compensarii se face prin
diferentele dintre orientarile calculate pe baza directiilor
azimutale compensate si a unghiului de orientare compensat al
statiei(tabelul 1.12 ,coloana 4) si orientarile directiilor
calculate din coordonatele compensate ale punctului nou si coordonatele
punctelor vechi (tabelul 1.18, coloana 4). Comparatia dintre cele
doua siruri de valori releva egalitatea marimilor si
deci, corectitudinea calculului.
(2007-1002) θ 2007-i-
θc 2007-i = 327g 51c 11cc,23
- 327g 51c 11cc,23
= 0cc,00
(2007-1004) θ 2007-i- θc
2007-i = 346g 37c 64cc,96 - 346g
37c 64cc,96 = 0cc,00
(2007-1007) θ 2007-i- θc
2007-i = 356g 19c 86cc,32 - 356g
19c 86cc,32 = 0cc,00
(2007-1010) θ 2007-i- θc
2007-i = 71g 11c 49cc,13 - 71g
11c 49cc,13 = 0cc,00
(2007-1012) θ 2007-i- θc
2007-i = 196g 21c 42cc,20 - 196g
21c 42cc,20 = 0cc,00
Cu operatia de verificare, procesul compensarii
coordonatelor punctelor noi, determinate prin metoda masuratorilor
indirecte este incheiat.
Calculul erorii medii patratice a unei singure
masuratori directe
Pentru evaluarea preciziei in pozitia pe plan
a punctului nou 100, se calculeaza mai intai eroarea medie
patratica a unei singure masuratori directe de aceeasi
precizie, cu relatia:
s0
= ±
 = ±
= ±
 = ± 0cc,19
= ± 0cc,19
Valoarea obtinuta reprezinta eroarea post-compensare a unei
directii masurata pe teren cu aceeasi precizie. La
numitor r = 5 numarul
ecuatiilor initiale de corectii (numarul directiilor
masurate) iar n = 3 numarul necunoscutelor dx,dy,dz.
Calculul erorilor medii patratice ale
marimilor compensate ale necunoscutelor si erorii totale in pozitia punctului pe plan
Erorile medii patratice ale masuratorilor compensate ale
necunoscutelor dx si dy, reprezinta erorile de determinare a celor
mai probabile valori ale coordonatelor punctului nou, numite coordonate
compensate X100 si Y100. Astfel, erorile medii ale
abscisei si ale ordonatei
punctului noi sunt calculate cu relatiile
sx = ± s0
 ; sy = ± s0
; sy = ± s0

unde :
s0 - eroarea medie
patratica a unei singure masuratori directe de aceeasi
precizie;
Q11, Q22 -
coeficietii de pondere patratici ale celor doua necunoscute (dx,
dy).
Se calculeaza coeficietii de pondere
patratici cu formulele
Q11 =
 = 1.25
= 1.25
Q22 =
 = 0.45
= 0.45
dupa
care, erorile medii patratice sunt
sx = ± s0
 = ± 0cc,19
= ± 0cc,19
 = ± 0.20 075dm.
= ± 20 .75mm.
= ± 0.20 075dm.
= ± 20 .75mm.
sy = ± s0
 = ± 0cc,19
= ± 0cc,19
 = ± 0.12742dm. = ± 12.42 mm.
= ± 0.12742dm. = ± 12.42 mm.
Ele reprezinta erorile in pozitia punctului de-a lungul axelor de
coordonate. Pe baza lor se calculeaza eroarea totala in pozitia punctului cu formula :
S2007 =
 = 24.19 mm.
= 24.19 mm.
Daca erorile sx si sy pot fi pozitive
si negative, eroarea totala este esential pozitiva.
Dezavantajul erorilor medii patratice consta in faptul ca, ele
nu permit cunoasterea directiilor de-a lungul carora erorile
sunt maxime si minime, respectiv marimile acestora. Acest lucru se
poate cunoaste cu ajutorul elipsei erorilor si a podarei elipsei
erorilor.
Calculul
elementelor elipsei erorilor si ale podarei elipsei erorilor pentru punctul nou
Se calculeaza orientarile directiilor reciproc
perpendiculare de-a lungul carora erorile vor fi maxime si minime, cu
ajutorul ecuatiei trigonometrice :
2θ = arctg

Coeficientul de pondere dreptunghiular este:
Q12 =
 = -0.47
= -0.47
Se introduce in ecuatia de mai sus, rezultand
2θ
= arctg
 =
=
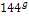
Unghiul de
orientare se considera de la sistemul de axe in care a fost determinat
punctul nou, mai precis de la axa X.
In continuare,
se calculeaza marimile semiaxelor elipselor de eroare. Mai intai se
calculeaza coeficientul :
q =
 = 0.94
= 0.94
iar pe baza lui, marimile
semiaxelor elipsei :
A = ± s0
 = ± 0.2131 dm.
= ± 21.31mm
= ± 0.2131 dm.
= ± 21.31mm
B = ± μ
 = ± 0.1143 = ± 11.43
mm
= ± 0.1143 = ± 11.43
mm
Pentru desenarea podarei (curba
pedala) generata de elipsa erorilor, se calculeaza razele -
vector ale podarei, cu ajutorul semiaxelor elipsei si pentru diferite
valori ale unghiului ψ, facut de semiaxa mare cu raza - vector, cu
formula :
Sψ
=
 , ψ
, ψ
 [ 0g , 400g ]
[ 0g , 400g ]
Calculele se conduc in tabelul IV.14, pentu valori ale unghiului ψ din
10g in 10g . Podara fiind simetrica fata
de axele elipsei erorilor, calculul razelor - vector se executa numai
pentru unghiurile primului cadran si sunt exprimate in milimetri.
Tabelul 1.19
|
Pct.
|
Unghi
Ψg
|
Semiaxe -elipsa
|
Raza-vector
SΨ
(mm)
|
|
A
(mm)
|
B
(mm)
|
|
|
|
|
|
|
a
|
|
|
|
|
|
c
|
|
|
|
d
|
|
|
|
e
|
|
|
|
f
|
|
|
|
g
|
|
|
|
h
|
|
|
|
i
|
|
|
|
j
|
|
|
|
k
|
|
|
|
b
|
|
|
Constructia grafica a
podarei elipsei erorilor la scara 3:1
Constructia grafica a
podarei elipsei erorilor, numita si curba pedala sau curba
erorilor medii patratice, se face la o scara supraunitara, in
cazul de fata 3:1, pe baza orientarilor semiaxelor elipsei de
eroare si ale datelor tabelului 1.19, in urmatoarea succesiune :
se
considera pe plan punctul nou determinat si se duc axele sistemului
initial
X,Y in care a
fost determinat punctul ;
cu
ajutorul unghiurilor de orientare θ si θ + 100g,
masurate fata de axa X, se
duc axele XA
si YA, care corespund directiilor de-a lungul carora
erorile sunt maxime si minime. De-a lungul acestor axe, incepand din
origine, se iau la scara 3:1 segmentele care corespund semiaxelor elipsei
erorilor A = 21.31mm si B = 11.43 mm, obtinandu-se punctele a, pe axa
XA, si b, pe axa YA ;
se
aplica fata de axa XA, unghiurile ψ (10g,
20g, 30g, . , 100g) iar pe directiile
obtinute
se aplica la scara lungimile razelor - vector (tabelul 1.19),
obtinandu-se punctele c,d . ,k ;
se
unesc punctele principale a si b cu punctele intermediare c,d, . ,k printr-o
curba
plana, obtinandu-se curba podara pentru primul cadran.
In
celelalte cadrane, constructia grafica a podarei se face pe baza
simetriei,
in raport cu
axele XA si YA ;
Reprezentarea grafica a podarei elipsei erorilor a fost realizata
in programul de grafica pe calculator, AutoCAD 2008.(figura 1.7 pentru
punctul 2007).
Configuratia podarei elipsei erorilor este in functie de
configuratia elipsei erorilor, de raportul celor doua semiaxe. Cand
raportul este egal cu unitatea (A/B = 3),
elipsa si podara degenereaza intr-un cerc de eroare. Pe
masura ce raportul creste, aria podarei difera tot mai mult
de aria elipsei. De asemenea, pentru elipse de aceeasi arie, dar de
configuratie diferita, din cauza raportului semaixelor, ariile podarelor
difera sensibil.
Prin masurare grafica, in progranul de grafica, se pot
determina sau doar verifica, marimile erorilor medii ale coordonatelor
compensate ale punctului, de-a lungul
axelor de coordonate. Astfel, pentru eroarea sx se masoara
segmentul intre origine si punctul unde podara intersecteaza axa X;
la fel, pentru eroarea sy se masoara segmentul dintre
punctul 2100 si punctul unde podara intersecteaza axa Y. Se
obtin :
sx = ± 0.06 mm.
sy
= ± 0.12 mm.
Valorile obtinute pe cale grafica, cu ajutorul podarelor sunt
egale cu cele rezultate prin calcul la punctul , respectiv :
sx
=
 = 0.18 / 3
= ± 0.9 mm.
= 0.18 / 3
= ± 0.9 mm.
sy
=
 = 0.36 / 3 = ±
1.7 mm.
= 0.36 / 3 = ±
1.7 mm.
Raportul dintre erorile maxime si minime fiind A / B 2,90
Aria podarei elipsei erorilor caracterizeaza domeniul de situare a
pozitiei probabile a punctului nou cu o probabilitate mai mare decat in
cazul in care se considera aria elipsei erorilor.
Astfel, aria elipsei erorilor este de:
Ae = πAB =0.034mm
pe cand aria podarei generata
de elipsa este de
Ap =
 = 0.056mm
= 0.056mm
Calculul
erorilor medii patratice ale marimilor compensate ale
orientarilor si
distantelor dintre punctul
nou si punctele vechi.
In practica compensarii retelelor geodezice de triangulatie
prin metoda masuratorilor indirecte, variatia coordonatelor, la
calculul erorilor medii patratice ale functiilor de valorile
compensate ale coordonatelor punctelor noi se foloseste expresia erorii
unei functii de marimile compensate ale coordonatelor punctelor noi,
sau chiar expresia erorii functiei de functii. Este cazul
aflarii erorilor medii patratice ale orientarilor si
distantelor dintre puncte.
a. Eroarea medie patratica a
marimii compensate a orientarii a unei directii. Orientarea compensata a unei directii se
exprima prin orientarea provizorie si corectiile coordonatelor
(necunoscutele). Pentru orientarea directiei dintre un punct nou si
un punct vechi, se considera relatia :
θ2007-i = θo2007-i + dθ2007-i = θo2007-i
- ai dx - bi dy
Aceasta relatie corespunde
formulei generale a unei functii de marimile compensate ale
necunoscutelor :
F =
fo + f1 dx +f2 dy ,
unde coeficientii vor fi : fo = θo2007-i
, f1 = - ai , f2 = - bi
Se calculeaza, mai intai, coeficientul de pondere al functiei
(inversa ponderei) cu relatia folosind coeficientii de pondere ai
necunoscutelor :
Qθ
 = f12
Q11 + 2 f1f2 Q12 + f22
Q22 = ai2 Q11 + 2 aibi
Q12 + bi2 Q22
= f12
Q11 + 2 f1f2 Q12 + f22
Q22 = ai2 Q11 + 2 aibi
Q12 + bi2 Q22
dupa care,
se calculeaza eroarea medie patratica a orientarii
compensate (a functiei) :
sθ
 = ± s0
= ± s0

Pentru toate directiile intre punctul
nou si punctele vechi s-au calculat erorile medii patratice ale
marimilor compensate ale orientarilor, rezultatele fiind cuprinse in
tabelul 1. 20
|
Tabel 2.20
|
|
Directia
|
Orientarea
Compensata
|
Coeficient
de pondere
Qθ
|
Er.med.
Patratica
s

|
Er. med.
patratica
s

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eroarea medie patratica a
orientarii compensate a directiei se poate determina mult mai simplu,
prin masurare grafica cu ajutorul curbei podare (Figura 1.7). Pentru
aceeasi directie, din punctul 2007 ridica o perpendiculara
pe directia 2007-1002 , care va intalni curba podara intr-un punct n,
si se masoara grafic, in programul de grafica , segmentul 2007-n
. Cunoscandu-se lungimea laturei (distanta provizorie) Do2007-1002, din
tabelul 1.12, eroarea medie patratica a orientarii se va calcula
cu formula :
sθ
 = ± ρcc
= ± ρcc

Valoarea obtinuta este egala cu cea calculata analitic
(tabelul 1.12), precizia determinarilor grafice fiind aceeasi cu cea din calculul analitic.
b.
Eroarea medie patratica a marimii
unei distante compensate Distanta
compensata dintre un punct nou si un punct vechi, se poate exprima
prin distanta provizorie si corectiile coordonatelor, sub forma
functiei :
 =D2007-i
= Do2007-i + f '1 dx + f '2 dy = f
'o + f '1 dx + f '2 dy
=D2007-i
= Do2007-i + f '1 dx + f '2 dy = f
'o + f '1 dx + f '2 dy
unde : i= punct vechi, f 'o = Do2007-i
- distanta provizorie, calculata in tabelul 2.11, iar ceilalti
coeficienti constanti sunt dati de marimile derivatelor
partiale in jurul valorii provizorii a distantei :
f'1 =
 = - cos θo2007-i
; f '2 =
= - cos θo2007-i
; f '2 =
 = - sin θo2007-i
= - sin θo2007-i
Se calculeaza coeficientul de pondere al distantei considerate
(al functiei), folosindu-se relatia cu coeficientii de pondere
ai necunoscutelor :
QD
 = f '12
Q11 + 2 f '1f '2 Q12 + f '22
Q22
= f '12
Q11 + 2 f '1f '2 Q12 + f '22
Q22
QD
 = cos2
θo2007-i Q11 + 2 cos θo2007-i
sin θo2007-i Q12 + sin2 θo2007-i
Q22
= cos2
θo2007-i Q11 + 2 cos θo2007-i
sin θo2007-i Q12 + sin2 θo2007-i
Q22
Eroarea medie patratica a distantei compensate (a
functiei), va fi :
sD
 = ± s0
= ± s0

In acest mod s-a procedat pentru calculul erorilor medii ale tuturor distantelor
compensate, rezultatele fiind prezentate in tabelul 1.21.
|
Tabel 1.21
|
|
Directia
|
Distanta
compensata
D(m)
|
Coeficient
de pondere

|
Er.med.
patratica

|
Er. Med.
Patratica
 (mm)
(mm)
|
Erori
Relative
1: R
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Erorile medii patratice ale distantelor compensate se pot
obtine mult mai simplu, prin masurare grafica. Astfel, pentru
distanta D2007-1002, se masoara in programul de
grafica, distanta de la origine (punctul 2007) la punctul o, unde
podara intersecteaza directia spre punctul 1002. Astfel, se
obtine :
sD
 =
=
 / 3
/ 3
valoare
egala cu cea obtinuta prin calcul (s
 ), dar mai rapid.
), dar mai rapid.
In final, pentru distantele
compensate, s-au calculat si erorile relative, cu relatia
cunoscuta :
Er
=
 =
=
 =
=
 = 1 : R ,
= 1 : R ,
valorile obtinute fiind trecute in tabelul 1.21,
coloana 6