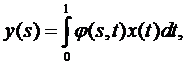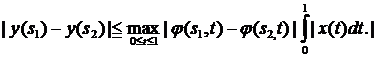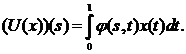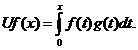Matematica aplicata, Anul I
Analiza functionala
OPERATORI COMPACTI
DEFINITIA SI PROPRIETATILE
OPERATORILOR COMPACTI
Fie 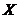 si
si  spatii liniare
normate.
spatii liniare
normate.
Definitia 1.1 Un operator liniar  se numeste compact (complet continuu), daca pentru orice
multime marginita
se numeste compact (complet continuu), daca pentru orice
multime marginita 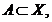 multimea
multimea 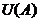 este relativ compacta in
este relativ compacta in 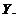
Daca un operator liniar 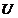 este compact, atunci el este si continuu.
este compact, atunci el este si continuu.
Intr-adevar,
daca 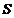 este sfera unitate
inchisa in
este sfera unitate
inchisa in 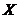 , atunci
, atunci 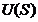 este marginita
si
este marginita
si 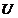 este continuu.
este continuu.
Vom nota cu 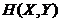 multimea
operatorilor liniar compacti care aplica
multimea
operatorilor liniar compacti care aplica 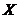 in
in  .
.
Teorema 1.1 Daca 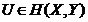 , iar
, iar 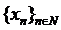 este un sir de
elemente din
este un sir de
elemente din 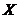 care converge slab
catre
care converge slab
catre  , atunci
, atunci 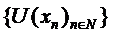 converge in norma
catre
converge in norma
catre 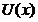 .
.
Demonstratie. Notam 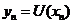 si
si 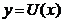 . Sa presupunem ca sirul
. Sa presupunem ca sirul 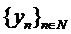 nu converge in
norma catre
nu converge in
norma catre 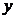 . Exista atunci un numar
. Exista atunci un numar 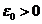 si un sir
crescator
si un sir
crescator 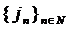 de numere naturale
asa ca
de numere naturale
asa ca
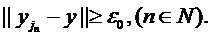
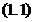
Pe de alta parte,
sirul 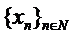 fiind slab convergent
este marginit. Deci si subsirul
fiind slab convergent
este marginit. Deci si subsirul 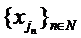 este marginit. Dar atunci
este marginit. Dar atunci 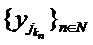 care converge in norma
si deci si slab catre un element
care converge in norma
si deci si slab catre un element 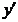 . Deci
. Deci 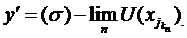 Cum insa
Cum insa 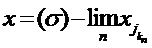 rezulta
rezulta 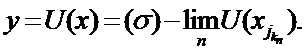
Rezulta 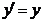 , adica
, adica 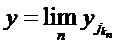 in norma) ceea ce este in contradictie cu
in norma) ceea ce este in contradictie cu
Teorema 1.2 Multimea 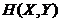 este un subspatiu
liniar al spatiului
este un subspatiu
liniar al spatiului 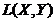 .
.
Demonstratie.
Fie
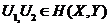 si
si 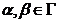 . Notam
. Notam 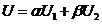 . Fie
. Fie 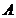 o submultime
marginita a lui
o submultime
marginita a lui 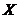 si
si 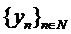 un sir de
elemente din
un sir de
elemente din 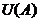 . Fie
. Fie 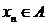 asa ca
asa ca 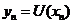 si sa
notam
si sa
notam 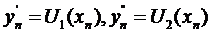 . Operatorul
. Operatorul 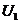 fiind compact,
sirul
fiind compact,
sirul 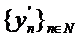 contine un subsir
convergent
contine un subsir
convergent 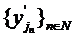 ; operatorul
; operatorul 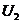 fiind compact,
sirul
fiind compact,
sirul 
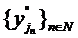 contine un
subsir convergent
contine un
subsir convergent 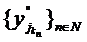 . Deoarece
. Deoarece
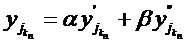
sirul 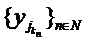 este convergent.
Multimea
este convergent.
Multimea 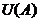
 este deci relativ compacta si in concluzie
este deci relativ compacta si in concluzie 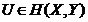 .■
.■
Teorema 1.3 Daca  este un spatiu
Banach, atunci
este un spatiu
Banach, atunci 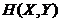 este un subspatiu liniar inchis al spatiului
este un subspatiu liniar inchis al spatiului 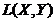 .
.
Demonstratie. Fie 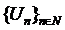 un sir de
elemente din
un sir de
elemente din 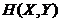 si
si 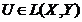 asfel ca
asfel ca  in
in 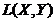 . Sa aratam ca
. Sa aratam ca 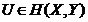 .
.
Pentru aceasta este
suficient sa demonstram ca daca 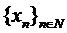
 este un sir marginit de elemente din
este un sir marginit de elemente din 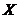 , atunci
, atunci 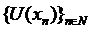 contine un
subsir convergent.
contine un
subsir convergent.
Consideram deci
sirul marginit 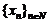 . Exista un subsir
. Exista un subsir 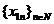 al sirului
al sirului 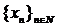 asfel incat
asfel incat 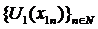 sa fie
convergent. Din
sa fie
convergent. Din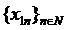 se poate extrage un subsir
se poate extrage un subsir 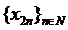 astfel incat
astfel incat 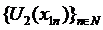 sa fie
convergent. Continuand procedeul si notand
sa fie
convergent. Continuand procedeul si notand 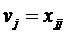 , sirul
, sirul 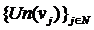 este convergent,
este convergent,  .
.
Avem apoi
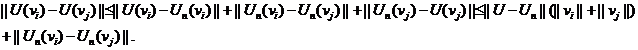 Sirul
Sirul 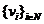 fiind
marginit exista
fiind
marginit exista 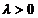 astfel incat
astfel incat 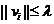 , deci
, deci
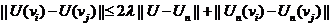
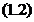
Deoarece  , pentru orice
, pentru orice 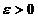 exista
exista 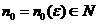 astfel incat
astfel incat
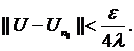
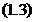
Pe de alta parte, sirul 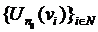 fiind convergent, este
un sir Cauchy, deci exista
fiind convergent, este
un sir Cauchy, deci exista 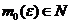 asfel incat
asfel incat
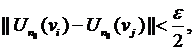
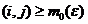
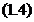
Daca in 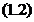 inlocuim
inlocuim 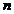 cu
cu  si tinand
seama de
si tinand
seama de 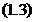 si
si 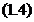 obtinem
obtinem
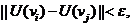
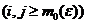
Deci 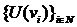 este un sir
Cauchy. Spatiul
este un sir
Cauchy. Spatiul  fiind complet, exista
fiind complet, exista 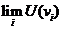 , deci
, deci 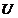 este compact. ■
este compact. ■
Fie 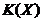 multimea tuturor
operatorilor compacti care aplica
multimea tuturor
operatorilor compacti care aplica 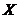 in
in 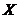 si
si 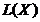 , multimea tuturor operatorilor liniari si continui
care aplica
, multimea tuturor operatorilor liniari si continui
care aplica 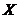 in
in 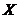 .
.
Teorema
1.4 Daca 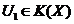 si
si 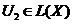 , atunci
, atunci 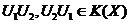 .
.
Demonstratie. Deoarece 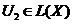 rezulta ca
multimea
rezulta ca
multimea 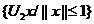 este marginita si atunci, intrucat
este marginita si atunci, intrucat 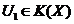 rezulta
ca multimea
rezulta
ca multimea 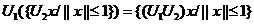 este relativ
compacta. Deci
este relativ
compacta. Deci 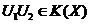 .
.
Fie acum un sir
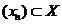 astfel incat
astfel incat  ,
,  . Cum
. Cum 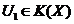 rezulta ca exista un subsir
rezulta ca exista un subsir 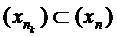 astfel incat
sirul
astfel incat
sirul 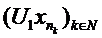 este convergent.
este convergent.
Deoarece 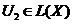 rezulta ca
sirul
rezulta ca
sirul 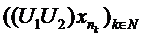 este convergent. Prin
urmare,
este convergent. Prin
urmare, 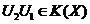 .
.
2. ADJUNCTUL UNUI OPERATOR COMPACT
Fie 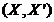 si
si 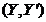 doua perechi
duale de spatii liniare si un operator liniar
doua perechi
duale de spatii liniare si un operator liniar  .
.
Definitia 2.1 Se numeste adjunctul (sau dualul) lui 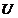 , operatorul
, operatorul 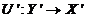 dat de formula:
dat de formula:
 ,
, 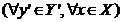 .
.
Operatorul U este evident liniar.
In teorema
urmatoare, pentru doua spattii liniare normate 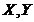 vom considera
perechile duale
vom considera
perechile duale 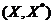 ,
,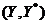 .
.
Teorema 2.1 Pentru ca un operator liniar si continuu 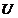 , care aplica un spatiu liniar normat
, care aplica un spatiu liniar normat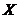 intr un spatiu
Banach
intr un spatiu
Banach  , sa fie un operator compact, este necesar si suficient ca adjunctul sau
, sa fie un operator compact, este necesar si suficient ca adjunctul sau 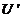 sa fie un
operator compact.
sa fie un
operator compact.
Demonstratie. 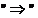 Sa notam cu
Sa notam cu 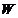 bila unitate
inchisa in spatiul
bila unitate
inchisa in spatiul  si fie
si fie 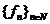 un sir de
elemente din
un sir de
elemente din 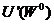 , deci
, deci 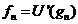 cu
cu 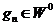 . Multimea
. Multimea 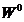 fiind slab
compacta,
fiind slab
compacta, 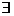 un subsir
un subsir 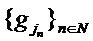 al sirului
al sirului 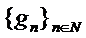 slab convergent
catre un element
slab convergent
catre un element 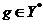 . Multimea
. Multimea 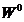 fiind egal
continua, sirul
fiind egal
continua, sirul 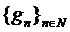 converge catre
converge catre 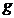 si in topologia
convergentei total marginite. Pe de alta parte, notand cu
si in topologia
convergentei total marginite. Pe de alta parte, notand cu 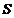 bila unitate
inchisa din saptiul
bila unitate
inchisa din saptiul 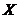 , multimea
, multimea 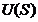 este relativ
compacta. Pentru orice numar
este relativ
compacta. Pentru orice numar 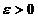 exista deci
exista deci 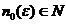 astfel ca
astfel ca
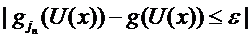 ,
, 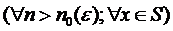 .
.
Rezulta 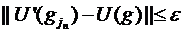
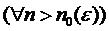 .
.
Punand acum 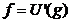 avem deci
avem deci
 ,
, 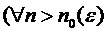 .
.
Prin urmare, 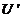 este operator
compact.
este operator
compact.
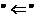 Suficienta
rezulta din faptul ca
Suficienta
rezulta din faptul ca 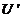 fiind operator
compact, adjunctul sau
fiind operator
compact, adjunctul sau 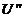 este de asemenea
operator compact si deci operatorul
este de asemenea
operator compact si deci operatorul 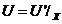 este compact.
este compact.
EXEMPLE DE OPERATORI COMPACTI
Spatiile considerate vor fi spatii
Banach reale.
3.1 Operatorul
matricial. Consideram spatiul 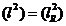 si operatorul
matricial
si operatorul
matricial
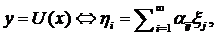
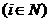
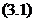
(unde 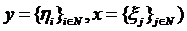 ) cu conditia ca seria dubla
) cu conditia ca seria dubla 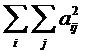 sa fie
convergenta.
sa fie
convergenta.
Acest operator este
compact.
3.2 Operatorul
integral. Notam 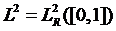 si
si 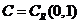 . Fie
. Fie  o functie
reala continua pe
o functie
reala continua pe 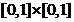 . Daca
. Daca 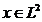 , atunci functia
, atunci functia
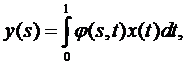
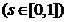
este continua,
deoarece
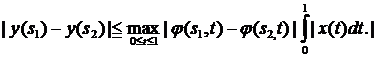
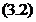
Sa consideram
operatorul 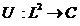 definit prin
definit prin
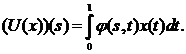
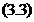
Acest operator este compact.
Observatii.
(1)
Daca prin (3.3) se considera operatorul 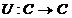 , atunci acest operator liniar este de asemenea compact.
, atunci acest operator liniar este de asemenea compact.
(2) Daca prin (3.3) se considera operatorul 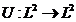 , atunci acest operator liniar este de asemenea compact.
, atunci acest operator liniar este de asemenea compact.
3.3 Pentru 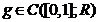 , definim operatorul liniar
, definim operatorul liniar 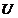 prin
prin
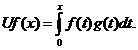
Operatorul 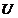 este operator compact.
este operator compact.
3.4 Operatorul
identitate este operator compact daca si numai daca spatiul
este finit dimensional.
BIBLIOGRAFIE
Analiza functionala, Romulus CRISTESCU, Editura didactica si
pedagogica, Bucuresti, 1983.
Analiza functionala, Danut RUSU.
https://en.wikipedia.org/wiki/Compact_operator


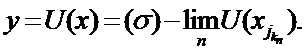
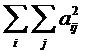 sa fie
convergenta.
sa fie
convergenta.