Divizibilitatea
in inele
Fie A un inel comutativ cu
element unitate. Se spune ca un element a A divide un element b
A divide un element b A (sau b este un multiplu al lui a) si se scrie a|b daca exista un elemnt c
A (sau b este un multiplu al lui a) si se scrie a|b daca exista un elemnt c A astfel ca b= ac. Daca a|b se mai spune ca a este
divizor al lui b, denumire care nu va fi folosita daca b=0.
A astfel ca b= ac. Daca a|b se mai spune ca a este
divizor al lui b, denumire care nu va fi folosita daca b=0.
Este clar ca
relatia de divizibilitate in A este o relatie binara care este
reflexiva, caci a|a , a=a·1 si tranzitiva caci din
a|b
si b|c rezulta b=ac, c= bc',
deci c=acc', adica a|c. Asadar,relatia de dvizibilitate este o relatie de
cuasiordine pe inelul A. Ea nu este insa in general o relatie de
ordine. In adevar, chiar in inelul 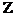 al intregilor
avem ca 1|-1 si -1|1,
insa 1
al intregilor
avem ca 1|-1 si -1|1,
insa 1 -1.
-1.
Direct din definitie
rezulta ca daca a,b,c 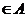 si a|b,
atunci a|bc, si daca in plus a divide si pe c, atunci a|(b+c).
De asemenea, daca a|(b+c) si a divide unul dintre termenii sumei el
divide si pe celalalt.
si a|b,
atunci a|bc, si daca in plus a divide si pe c, atunci a|(b+c).
De asemenea, daca a|(b+c) si a divide unul dintre termenii sumei el
divide si pe celalalt.
Daca a si b sunt elemente
in A astfel incat a divide b si b divide a, se spune ca a este
asociat cu b si vom scrie a~b. Relatia de asociere este o
relatie de echivalenta caci a~a, iar daca a~b, atunci
evident b~a. De asemenea, se verifica imediat ca relatia de
asociere este tranzitiva. In fapt aceasta relatie de
echivalenta este relatia de echivalenta asociata
relatiei de divizibilitate considarata ca o relatie de
cuasiordine (cap. I,2). Daca considram multimea factor in raport
cu aceasta relatie de echivalenta, atunci relatia de
divizibilitate introduce pe aceasta multime o relatie de ordine.
Mai mult daca a~b si c~d,
rezulta ac~bd si atunci se constata ca pe multimea
factor putem introduce o operatie dedusa din operatia de
inmultire in A si cu care aceasta multime factor devine
semigrup. Multe dintre proprietatile divizibilitatii in
inelul A se reduc la studiul divizibilitatii in acest semigrup,
dupa cum se va vedea mai departe, caci aproape toate notiunile
si afimatiile raman adevarate pentru elemente asociate.
Acest fapt este o generalizare a aceluia ca studiul aritmeticii in 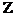 se reduce la
studiul acesteia in
se reduce la
studiul acesteia in 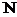 .
.
Lema
1.1. Fie A un inel si a, b doua elemente din A. Atunci A divide
pe b daca si numai daca aA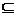 bA. In particular, a si b sunt asociate daca
si numai daca aA= bA.
bA. In particular, a si b sunt asociate daca
si numai daca aA= bA.
Demonstratie. Daca a
divide pe b , rezulta b=aa' cu a' A, deci b
A, deci b aA, de unde rezulta bA
aA, de unde rezulta bA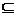 aA. Atunci in particular b
aA. Atunci in particular b aA, adica b=aa', cu a'
aA, adica b=aa', cu a' A
A
Propozitia
1.2 . Fie A un inel si a A. Atunci urmatoarele afirmatii sunt
echivalente:
A. Atunci urmatoarele afirmatii sunt
echivalente:
a)
a~1;
b)
a este element ireversibil in A;
c)
aA=A;
d)
a divide orice element al inelului A.
Demonstratie. a)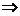 b). Din faptul ca a rezulta ca a divide pe 1,
adica exista a'
b). Din faptul ca a rezulta ca a divide pe 1,
adica exista a' A astfel ca 1=aa' si deci a este ireversabil in
A.
A astfel ca 1=aa' si deci a este ireversabil in
A.
Implicatia b) 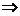 c) rezulta din propozitia III.c)
c) rezulta din propozitia III.c) 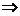 d) din lema precedenta, iar d)
d) din lema precedenta, iar d) 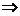 a) este evidenta.
a) este evidenta.
Propozitia precedenta
da o caracterizare a elementelor ireversabile dintr-un inel in
legatura cu divizibilitatea. Ea arata ca elementele
ireversabile ale inelului se comporta in raport cu divizibilitatea lafel
ca si elementul unitate al inelului; de aici provine denumirea lor de
unitati.
Propozitia
1.3. Fie A un inel integru. Atunci doua elemente a,b din A sunt
asociate daca si numai daca a=ub, unde u este elemnt ireversabil
in A.
Demonstratie. Daca a=ub,
unde u este element ireversabil in A, atunci este clar ca a si b sunt
asociate. Reciproc, sa presupunem ca a si b sunt asociate.
Atunci rezulta ca exista a', b'  A astfel ca b=ab' si a=ba', adica b=ba'b',
deci b(1-a'b')=0. Daca b=0, atunci evident si a=0 si totul este
demonstrat. In caz contrar, rezulta 1-a'b'=0 (caci A este integru),
deci a' si b' sunt elemente ireversabile in A.
A astfel ca b=ab' si a=ba', adica b=ba'b',
deci b(1-a'b')=0. Daca b=0, atunci evident si a=0 si totul este
demonstrat. In caz contrar, rezulta 1-a'b'=0 (caci A este integru),
deci a' si b' sunt elemente ireversabile in A.
Definitia
1.4. Fie A un inel si a,b elemente din A. Un element c A se numeste divizor comun al lui a si
daca c divide pe a si c divide pe b. Elementul d
A se numeste divizor comun al lui a si
daca c divide pe a si c divide pe b. Elementul d A se numeste cel mai mare divizor comun
(c.m.m.d.c) al elementelor a si b si se mai noteaza cu (a,b),
daca d este un divizor comun al elementelor a si b si pentru orice alt divizor comun d' al
elementelor a si b avem d' divide pe d.
A se numeste cel mai mare divizor comun
(c.m.m.d.c) al elementelor a si b si se mai noteaza cu (a,b),
daca d este un divizor comun al elementelor a si b si pentru orice alt divizor comun d' al
elementelor a si b avem d' divide pe d.
Un element n A se numeste multiplu comun al elementelor a,b
daca a divide pe n si b divide pe n. Elementul m
A se numeste multiplu comun al elementelor a,b
daca a divide pe n si b divide pe n. Elementul m A se numeste cel mai mic multiplu comun
(c.m.m.m.c) al elementelor a si b si se mai noteaza cu a,b] daca m este
multiplu comun al elementelor a si b si pentru orice multiplu comun m' al
elementelor a si b avem ca m divide pe m'.
A se numeste cel mai mic multiplu comun
(c.m.m.m.c) al elementelor a si b si se mai noteaza cu a,b] daca m este
multiplu comun al elementelor a si b si pentru orice multiplu comun m' al
elementelor a si b avem ca m divide pe m'.
Se spune ca doua elemente
a,b ale inelului A sunt relativ prime (sau prime intre ele) daca 1 este cel mai mare divizor comun
al lor.
Evident, definitiile date mai
sus pentru c.m.m.d.c si c.m.m.m.c. a doua elemente din inelul A ca
si definitia data elementelor relativ prime se
generalizeaza cu usurinta la un numar finit sau chiar
infinit de elemente ale inelului A si vor avea proprietati
analoage celor din cazul a doua elemente. Mentionam ca
pentru doua elemente arbitrare dintr-un inel oarecare se poate ca
c.m.m.d.c si c.m.m.m.c. sa nu existe, dupa cum vedea in cele ce
urmeaza. Insa daca c.m.m.d.c si c.m.m.m.c. a doua elemente
exista, atunci exista c.m.m.d.c si c.m.m.m.c. pentru un
numar finit de elemente.
Se observa ca daca
consideram relatia de divizibilitate ca o relatie de preordine,
atunci c.m.m.d.c al unei multimi de elemente este o margine
inferioara a acestei multimi si c.m.m.m.c. este o margine
superioara a acesteia.
Propozitia care urmeaza
exprima proprietati generale ale marginilor inferioare si
superioare pentru o multime cuasiordonata .
Propozitia
1.5. Fie A un inel
si a,b doua elemente din A.
i)
Daca
d A este cel mare divizor comun al elementelor a si
b , atunci un element d'
A este cel mare divizor comun al elementelor a si
b , atunci un element d' A este cel mai mare divizor comun al elementelor a
si b daca si numai daca este asociat cu d.
A este cel mai mare divizor comun al elementelor a
si b daca si numai daca este asociat cu d.
ii)
Daca
m este cel mai mic multiplu comun al elementelor a si b , atunci un elemet
m' A este cel mai mic multiplu comun al elemetelor a
si b daca si numai daca este asociat cu m.
A este cel mai mic multiplu comun al elemetelor a
si b daca si numai daca este asociat cu m.
Demonstratie. Vom demonstra doar afirmatia i),
caci ii) se demonstreaza analog. Din faptul ca d este cel mai
mare divizor comun al elementelor a si b , iar d' este cel mai mare
divizor al elementelor a si b rezulta ca d' divide pe d (pentru
ca d' este in particular divizor comun al elementelor a si b) si
divide d' (pentru ca in particular d este divizor comun al elementelor a
si b), adica d si d' sunt asociate. Reciproc, daca
presupunem d' asociat cu d, atunci din faptul ca d|a, d|b,d|d'
rezulta ca d' este divizor comun al elementelor a si b.
Fie acum c un divizor comun arbitrar
al elementelor a si b; atunci c|d (caci d este cel mai mare divizor
comun al elementelor a si b) si doarece d|d' rezulta c|d',
adica d' este cel mai mare divizor comun al elemntelor a si b.
Din aceasta propozitie
rezulta ca cel mai mare divizor comun si cel mai mic multiplu
comun a doua (sau mai multe) elemente dintr-un inel A sunt determinate
pana la o asociere.
Lema
1.6. Fie A un inel inegru si a,b doua elemente nenule. Daca
d este cel mai mare divizor comun al elementelor a si b si a=da',
b=db', atunci a', b' sunt relativ prime.
Demonstratie. Va fi suficient
sa aratam ca orice divizor comun al elementelor a' si
b' este ireversabil. Fie u un astfel de divizor; atunci du este divizor comun
al lui a si b , deci du divide pe d, adica d=duu', u' A. Deoarece d
A. Deoarece d 0, rezulta 1=uu', deci u este ireversabil.
0, rezulta 1=uu', deci u este ireversabil.
Lema
1.7. Fie A un inel
integru, a,b doua elemente nenule din A si d cel mai mare divizor
comun al a elementelor a si b. Daca pentru un element c  A, c
A, c 0, exista cel mai mare divizor comun al
elementelor ca si cb, atunci acesta este asociat cu cd (deci si cd
este cel mai mare divizor comun al elementelor ca si cb).
0, exista cel mai mare divizor comun al
elementelor ca si cb, atunci acesta este asociat cu cd (deci si cd
este cel mai mare divizor comun al elementelor ca si cb).
Demonstratie. Fie d' cel mai
mare divizor comun al elementelor ca si cb. Atunci din faptul ca cd
divide pe ca si cb divide pe d', deci d'=cdu, cu u A. Din ipoteza rezulta ca exista
A. Din ipoteza rezulta ca exista 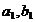 , a', b'
, a', b'  A astfel ca:
A astfel ca:
ca=d'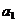 , a=da'
, a=da'
cb=d' , b=db'
, b=db'
din care
deduce relatiile:
cdu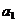 =cda'
=cda'
cdu =cdb'
=cdb'
si, deoarece cd  0
,rezulta:
0
,rezulta:
u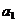 =a'
=a'
u =b'
=b'
deci u este divizor comun al elementelor a' si b', iar din lema
precedenta rezulta u element ireversabil in A.
Corolarul 1.8. Fie A un inel integru in care orice doua
elemente au c.m.m.d.c .
Daca a, b, c  A sunt astfel
incat a|bc si a este prim cu b rezulta ca a divide pe c.
A sunt astfel
incat a|bc si a este prim cu b rezulta ca a divide pe c.
In adevar, din (a,b)=1 si
din lema precendenta rezulta ca (ac,bc)=c. Cum a|ac si a|bc
rezulta ca a divide pe c.
Propozitia
1.9. Fie A un inel integru. Daca oricare doua elemente din A au
cel mai mare divizor comun , atunci oricare doua elemente din A au cel mai
mic multiplu cmun si produsul (a,b) [a,b] este asociat cu ab, pentru a,b  A, a
A, a 0, b
0, b 0.
0.
Demonstratie. Ne putem limita
la cazul in care a si b sunt elemente nenule. Fie d un cel mai mare
divizor comun al elementelor a si b si a=da', b=db', a',b'  A. Atunci
relatiile da'b'=ab'=a' arata ca m=da'b' este multiplu comun al
lui a si b. Fie m' un alt multipli comun al elementelor a,b.Deci m'=a
A. Atunci
relatiile da'b'=ab'=a' arata ca m=da'b' este multiplu comun al
lui a si b. Fie m' un alt multipli comun al elementelor a,b.Deci m'=a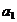 =da'
=da'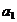 ,m'=d
,m'=d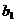 =db'
=db'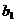 , cu
, cu 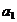 ,
,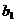
 A. De aici rezulta ca m este divizor comun al
elementelor m'a' si m'b', deci divide pe cel mai mare divizor comun al
acestor elemente, care este, conform lemei, egal cu m' (caci (a',b')=1).
Asadar, am aratat ca m este cel mai mic multiplu comun al
elementelor a si b si avem evident relatia md=ab.
A. De aici rezulta ca m este divizor comun al
elementelor m'a' si m'b', deci divide pe cel mai mare divizor comun al
acestor elemente, care este, conform lemei, egal cu m' (caci (a',b')=1).
Asadar, am aratat ca m este cel mai mic multiplu comun al
elementelor a si b si avem evident relatia md=ab.
Definitia
1.10. Fie a un element nenul si neireversabil ditr+un inel integru A. Se
spune ca a este ireductibil daca orice divizor al lui a este
sau asociat cu a sau este ireversabil (adica asociat cu 1) si reductibil in caz contrar.
Din aceasta definitie
rezulta ca daca a este un element ireductibil din inelul A si b
un element oarecare, atunci e'cel mai mare divizor comun al elementelor a
si b exista si este asociat cu a sau un element inversabil.
Propozitia
1.11. Intr-un inel integru A un element asociat cu un element ireductibil
este ireductibil.
Demonstratie.
Fie a un element ireductibil din A si b A un element asociat cu a. Atunci este clar ca b
A un element asociat cu a. Atunci este clar ca b 0 si b nu este ireversabil. Fie c un divizor al
lui b. Atunci c divide pe a, deci este sau asociat cu a, deci si cu b, sau
c este ireversabil, ceea ce demonstreaza afirmatia propozitiei.
0 si b nu este ireversabil. Fie c un divizor al
lui b. Atunci c divide pe a, deci este sau asociat cu a, deci si cu b, sau
c este ireversabil, ceea ce demonstreaza afirmatia propozitiei.
Propozitia 1.12. Fie A un inel integru si a A un element nenul si neinversabil in A. Atunci
urmatoarele afirmatii sunt echivalente:
A un element nenul si neinversabil in A. Atunci
urmatoarele afirmatii sunt echivalente:
a)
A
este ireductibil in a;
b)
daca
a=bc, atunci a este asocia cu cel putin unul dintre elementele b sau c;
c)
daca
a=bc, atunci a este asociat cu cel putin unul dintre elementele b sau c,
iar celalalt este inversabil.
Demonstratie. a)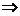 b). Din a=bc rezulta ca b este sau inversabil
sau asociat cu a; lafel c este sau inversabil sau asociat cu a. Insa nu se
poate ca ambele sa fie inversabile caci ar rezulta a inversabil.
b). Din a=bc rezulta ca b este sau inversabil
sau asociat cu a; lafel c este sau inversabil sau asociat cu a. Insa nu se
poate ca ambele sa fie inversabile caci ar rezulta a inversabil.
b) 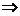 c). Fie a=bc. Din b) rezulta ca unul dintre
elementele b sau c, sa zicem b, este asociat cu a. Deci conform propozitiei 1.3, b=au cu u inversabil in A.
Atunci din a=auc si din faptul ca a
c). Fie a=bc. Din b) rezulta ca unul dintre
elementele b sau c, sa zicem b, este asociat cu a. Deci conform propozitiei 1.3, b=au cu u inversabil in A.
Atunci din a=auc si din faptul ca a 0 rezulta 1=uc, deci c este element inversabil.
Implicatia c)
0 rezulta 1=uc, deci c este element inversabil.
Implicatia c) 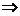 a) este evidenta.
a) este evidenta.
Datorita
proprietatilor b) si c) din propozitia precedenta,
uneori elementele ireductibile sunt numite nedecompozabile.
Definitia 1.13. Un element neinversabil si nenul p
din inelul integru A se numeste prim daca din faptul ca p|ab cu a,b A rezulta sau p|a sau p|b.
A rezulta sau p|a sau p|b.
Este clar ca orice element asociat cu un
element prim este si el prim.
Propozitia 1.14. Daca A este un inel integru ,
orice element prim din A este ireductibil.
Demonstratie. Fie p un element
prim in A. Atunci, daca p=ab, rezulta p|ab, deci p|a sau p|b. In
primu caz rezulta, evident, p asociat cu a, iar in cel de-al doilea p
asociat cu b. Reciproca acestei teoreme nu este intotdeauna
adevarata, insa propozitia urmatoare da o
conditie in care acest fapt are loc.
Propozitia 1.15. Fie A un inel integru in care orice
doua elemente au un cel mai mare divizor comun . Atunci in A orice element
ireductibil este prim.
Demonstratie. Fie q un elemnt
ireductibil si sa presupunem ca q|ab. Daca q|a totul s-a
terminat altfel, (q,a)=1 si din 1.8 rezulta q|b.
In inelul 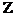 al intregilor
rationali numarul 2 este prim, deci si ireductibil. In
adevar, daca 2|ab, atunci trebuie ca cel putin unul dintre
numerele a sau b sa se divida cu 2, altfel produsul lor nu se divide
cu 2, caci daca a=2a'+1, b=2b'+1, atunci ab=4a'b'+2(b'+a')+1, care se
observa ca nu se divide cu 2. Analog se arata ca 3,5,7
etc. sunt numere prime, deci si
ireductibile. In acelasi timp se obtine ca -2,-3,-5 sunt si
ele ireductibile, fiind asociate cu cele precedente.
al intregilor
rationali numarul 2 este prim, deci si ireductibil. In
adevar, daca 2|ab, atunci trebuie ca cel putin unul dintre
numerele a sau b sa se divida cu 2, altfel produsul lor nu se divide
cu 2, caci daca a=2a'+1, b=2b'+1, atunci ab=4a'b'+2(b'+a')+1, care se
observa ca nu se divide cu 2. Analog se arata ca 3,5,7
etc. sunt numere prime, deci si
ireductibile. In acelasi timp se obtine ca -2,-3,-5 sunt si
ele ireductibile, fiind asociate cu cele precedente.
Fie k un corp. Atunci in inelul k[X] orice
polinom de gradul 1 este ireductibil. In adevar, daca f este un astfel de polinom, atunci din f=gh
rezulta g 0, h
0, h 0 si grad
0 si grad
(f)=grad(g)+grad(h)=1.
De aici rezulta ca sau grad (g)=1 si grad (h)=0, sau invers,
si afirmatia rezulta din faptul ca in k[X] un polinom de
gradul 0 este inversabil.
Elementul X din k[X] este prim in
k[X], caci daca X|fg, atunci este clar ca cel putin unul
dintre polinoamele f sau g se divide cu X.
Fie A un domeniu de
integritate a si a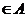 un element ireductibil. Atunci a este ireductibil si
in inelul A[X] caci
el este acolo, de asemenea, neinversabil si
un element ireductibil. Atunci a este ireductibil si
in inelul A[X] caci
el este acolo, de asemenea, neinversabil si  0 (elementele inversabile din A[X] fiind cele
inversabile in A[X]), iar daca a se descompune in produsul a doua
polinoame, acestea vor fi de grad 0, deci elemente din A.
0 (elementele inversabile din A[X] fiind cele
inversabile in A[X]), iar daca a se descompune in produsul a doua
polinoame, acestea vor fi de grad 0, deci elemente din A.
Sa consideram
acum inelul intregilor lui Gauss 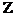 [i].
[i].
Pentru a studia in
continuare mai usor divizibilitatea in 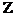 [i],
consideram functia N:C
[i],
consideram functia N:C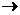 R, definita prin N(a+bi)=(a+bi)(a-bi)=
R, definita prin N(a+bi)=(a+bi)(a-bi)=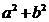 (N este numita functia norma, iar N(a) norma numarului
complex a).
(N este numita functia norma, iar N(a) norma numarului
complex a).
Daca,  atunci avem relatia:
atunci avem relatia:

In adevar, fie  =a+a'i,
=a+a'i,  =b+b'i; atunci:
=b+b'i; atunci:
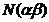 =N(ab-a'b'+(ab'+a'b)i)=(ab-a'b')
=N(ab-a'b'+(ab'+a'b)i)=(ab-a'b') +(ab'+a'b)
+(ab'+a'b) 
Iar
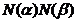
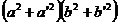
Si se verifica imediat egalitatea
ceruta. Evident, restictia lui N la 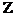 [i] are imaginea
cuprinsa in
[i] are imaginea
cuprinsa in 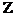 (chiar in N) si o vom nota tot cu N.
(chiar in N) si o vom nota tot cu N.
Sa vedem mai intai
care sunt elementele inversabile in 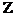 [i]. Fie
[i]. Fie  une element
inversabil. Atunci exista
une element
inversabil. Atunci exista  astfel ca
astfel ca 
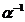 =1, de unde rezulta 1=N(1)=N(
=1, de unde rezulta 1=N(1)=N( )N(
)N(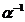 ) si deoarece N(
) si deoarece N( ) si N(
) si N(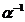 ) sunt numere naturale
) sunt numere naturale  1 rezulta ca N(
1 rezulta ca N( )=1. Reciproc, daca
)=1. Reciproc, daca 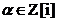 este un element astfel incat N(
este un element astfel incat N( )=1, atunci
)=1, atunci  este inversabil in
este inversabil in
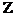 [i] caci avem
1= N(
[i] caci avem
1= N(

 unde
unde 
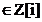 este conjugatul
lui
este conjugatul
lui  , deci
, deci  este inversul lui
este inversul lui  . Fie
. Fie  =a+bi,
a,b
=a+bi,
a,b 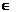 Z. Din cele de mai sus rezulta ca
Z. Din cele de mai sus rezulta ca  este element inversabil in
este element inversabil in 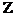 [i] daca
si numai daca N(
[i] daca
si numai daca N(
 , de unde rezulta ca elemente inversabile din
, de unde rezulta ca elemente inversabile din 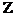 [i] sunt 1, -1,
i,-i.
[i] sunt 1, -1,
i,-i.
Din propozitia 1.3
rezulta ca daca  si
si  sunt elemente
asociate in
sunt elemente
asociate in 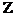 [i], atunci N(
[i], atunci N(
 . Sa mai observam ca daca
. Sa mai observam ca daca 
 , atunci N(
, atunci N(
 . Reciproc, este adevarata urmatoarea
lema.
. Reciproc, este adevarata urmatoarea
lema.
Lema 1.16.
Daca  si
si 
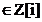 sunt astfel incat
sunt astfel incat 
 si N(
si N(
 , atunci
, atunci  este asociat cu
este asociat cu 
Demonstratie. Daca =0,afirmatia este evidenta. Pentru
=0,afirmatia este evidenta. Pentru 
 0 , din faptul ca
0 , din faptul ca |
| rezulta
rezulta  '
' 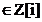 astfel incat
astfel incat =
=
 '. Avem atunci
'. Avem atunci  ,
deci
,
deci  =1, adica
=1, adica  ' este inversabil in
' este inversabil in 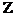 [i] si lema
este demonstrata.
[i] si lema
este demonstrata.
In 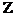 [i] numarul 2
este reductibil caci el se scrie sub forma 2=(1+i)(1-i), iar 1+i si
1-i nu sunt inversabile caci N(1+i)= N(1-i)=2.
[i] numarul 2
este reductibil caci el se scrie sub forma 2=(1+i)(1-i), iar 1+i si
1-i nu sunt inversabile caci N(1+i)= N(1-i)=2.
Sa aratam acum ca 1+i si 1-i
sunt elemente ireductibile in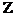 [i] . Fie 1+i=
[i] . Fie 1+i=
 . Atunci 2= N(1+i)=
. Atunci 2= N(1+i)= 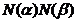 si avem deci
o descompunere in Z a lui 2,de unde
rezulta sau N(
si avem deci
o descompunere in Z a lui 2,de unde
rezulta sau N( )=2 si N
)=2 si N =1, sau invers. Deci, conform lemei de mai sus sau
=1, sau invers. Deci, conform lemei de mai sus sau este asociat cu 1+i in
este asociat cu 1+i in ,sau
,sau  este asociat cu 1+i. Asadar 1+i este element ireductibil in
este asociat cu 1+i. Asadar 1+i este element ireductibil in  . Pentru 1-i rationamentul este analog.
. Pentru 1-i rationamentul este analog.
Numarul 3 in  este ireductibil.
In adevar, daca ar fi ireductibil ar exista o descompunere a sa de
forma 3=
este ireductibil.
In adevar, daca ar fi ireductibil ar exista o descompunere a sa de
forma 3=
 , in care
, in care  si
si  sunt
neinversabile. Atunci obtinem ca 9=N(3)=
sunt
neinversabile. Atunci obtinem ca 9=N(3)= 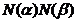 , de unde rezulta
, de unde rezulta 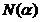 =3 si
=3 si  =3, deoarece am presupus ca
=3, deoarece am presupus ca  si
si  sunt
neinversabile. Fie
sunt
neinversabile. Fie  =a+bi.
Atunci:
=a+bi.
Atunci:
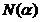 =
=
Deci  a si se observa ca nu exista numere
intregi a,b care sa verifice aceasta egalitate, deci un astfel de
a si se observa ca nu exista numere
intregi a,b care sa verifice aceasta egalitate, deci un astfel de  nu exista
si prin urmare 3 este ireductibil in
nu exista
si prin urmare 3 este ireductibil in  .
.
Consideram inelul  ;acesta este format din toate elementele
;acesta este format din toate elementele 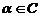 care se scriu sub forma a+bi
care se scriu sub forma a+bi , unde a, b
, unde a, b Z. Definim si aici functia N:
Z. Definim si aici functia N: 
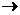 N (numita functie norma) prin
N (numita functie norma) prin 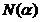 =
=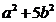 , unde
, unde  = a+bi
= a+bi .Se verifica imediat acesta functie este
multiplicativa, adica pentru
.Se verifica imediat acesta functie este
multiplicativa, adica pentru  ,
, 

 avem
avem

de unde
rezulta ca daca 
 , atunci
, atunci 
Ca si pentru
inelul intregilor lui Gauss, avem ca un element

 este
inversabil daca si numai daca
este
inversabil daca si numai daca 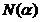 , rationamentul fiind intrutotul analog. Fie
, rationamentul fiind intrutotul analog. Fie  = a+bi
= a+bi
 este inversabil daca si numai daca
este inversabil daca si numai daca 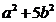 =1, de unde rezulta ca in acest inel elementele
inversabile sunt 1 si -1. Se observa, de asemenea, ca si
pentru acest inel ramane valabila lema.
=1, de unde rezulta ca in acest inel elementele
inversabile sunt 1 si -1. Se observa, de asemenea, ca si
pentru acest inel ramane valabila lema.
Sa consideram
acum elemental 3 din acest inel . 3 este ireductibil,
caci daca 3=
 si
si  si
si neinversabile rezulta ca 9=
neinversabile rezulta ca 9=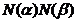 , adica
, adica 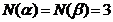 . Daca
. Daca  = a+bi
= a+bi , atunci avem 3=
, atunci avem 3=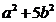 , ceea ce nu este posibil. Insa 3 nu este un
numar prim in acest inel caci
, ceea ce nu este posibil. Insa 3 nu este un
numar prim in acest inel caci  , iar 3 nu divide nici unul dintre factori. Daca ar
divide de exemplu pe
, iar 3 nu divide nici unul dintre factori. Daca ar
divide de exemplu pe 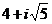 , ar rezulta ca N(3)=9 ar divide pe N
, ar rezulta ca N(3)=9 ar divide pe N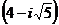 =21. Acest exemplu arata ca reciproca
propozitiei 1.14 nu este intotdeauna adevarata, adica nu in
orice inel integru un element ireductibil este prim. Deducem, de asemenea, ca in
=21. Acest exemplu arata ca reciproca
propozitiei 1.14 nu este intotdeauna adevarata, adica nu in
orice inel integru un element ireductibil este prim. Deducem, de asemenea, ca in  nu oricare
doua elemente au un c.m.m.d.c.
nu oricare
doua elemente au un c.m.m.d.c.

