Inelul claselor
de resturi modulo n
Operatiile
de adunare si inmultire confera multimii Z a numerelor
intregi o structura de inel comutativ unitar si fara divizori ai lui zero .(pe scurt inel integru
) .In acest inel multimea nZ a multiplilor numarului natural n
(fixat) formeaza un ideal (bilateral) . Pe de alta parte daca I
este un ideal al inelului (Z, +, ) atunci I este un
subgrup al grupului (Z, +) deci exista un numar natural n astfel
incat I = nZ . Daca I = nZ si
J = mZ sunt doua ideale ale lui Z atunci I + J este de asemenea un ideal
al lui Z si exista d I Z astfel incat I + J =
dZ sau nZ + mZ = dZ (putem presupune d I N) . Din relatia n
m I dZ rezulta d n si d m , iar din relatia d I nZ + mZ rezulta ca
exista a, b I Z astfel incat d = an +
bm . Din urma relatiei deducem ca orice divizor comun al lui m
si n este si un divizor al lui d . Prin urmare d este cel mai mare
divizor comun al numerelor intregi n
si m . Analog se demonstreaza ca daca nZ mZ = qZ atunci q este cel mai
mic multiplu comun al lui n si m . De asemenea are loc relatia (nZ)(mZ) = (nm)Z .
Inelele
factor ale inelului Z se construiesc prin factorizare cu ideale care au forma
nZ , n I N . Reamintim ca
pornind de la structura de grup aditiv a lui Z si considerand un subgrup
nZ al acestuia , relatia
x y x - y I nZ
este o relatie de echivalenta (numita
si relatie de congruenta modulo n ) si notata in
teoria numerelor prin x s z (mod n) ale carei
clase de echivalenta au forma
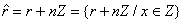
Clasele de
echivalenta se mai numesc si clase de resturi modulo n , in
rolul reprezentantului r putand fi ales totdeauna un numar natural cuprins
intre 0 si n - 1 . Multimea acestor clase Zn = capata o structura de grup comutativ in raport cu
operatia 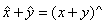 Constructia amintita tine
seama numai de operatia de adunare pe Z . Tinand
cont si de operatia de inmultire din Z , deci de structura de
inel , se poate completa si structura lui Zn . Astfel operatia
Constructia amintita tine
seama numai de operatia de adunare pe Z . Tinand
cont si de operatia de inmultire din Z , deci de structura de
inel , se poate completa si structura lui Zn . Astfel operatia
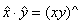
impreuna cu operatia de adunare induc pe Zn o
structura de inel comutativ si unitar Acest inel poarta numele
de inelul claselor de resturi modulo n . Elementele remarcabile ale acestui
inel sunt urmatoarele : 0 - elementul neutru (al operatiei de adunare
) , 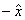 - opusul clasei
- opusul clasei 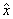 ,
, 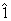 - elementul unitate (al
operatiei de inmultire ) .
- elementul unitate (al
operatiei de inmultire ) .
Aplicatia jn : Z Zn definita prin jn (x) = 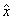 este un morfism unitar de inele deoarece :
este un morfism unitar de inele deoarece :
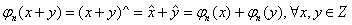
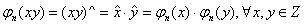
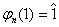
Morfismul jn se numeste surjectia
canonica a lui Z pe inelul sau
factor Zn . Daca n = 0 atunci
fiecare clasa de resturi in Z0 este
de forma 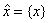 . Surjectia
canonica j0 = Z Z0 este si injectiva ,
deci inelele Z si Z0 sunt canonic izomorfe .
. Surjectia
canonica j0 = Z Z0 este si injectiva ,
deci inelele Z si Z0 sunt canonic izomorfe .
Daca n
= 1 atunci 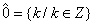 = Z , deci toate numerele intregi fac parte
dintr-o singura clasa de resturi , iar inelul Z1 este inelul nul , Z1
=
= Z , deci toate numerele intregi fac parte
dintr-o singura clasa de resturi , iar inelul Z1 este inelul nul , Z1
= 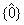 .
.
Inelul Zn are mai multe aplicatii in teoria numerelor
. In continuare , pe baza proprietatilor grupurilor finite vom deduce
cateva astfel de rezultate . Pentru aceasta vom stabilii mai intai care sunt
unitatile (elementele inversabile ) inelului Zn .
Teorema
6.1. In inelul Zn , n > 1, elementul 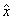 este inversabil daca si numai
daca x si n sunt relativ prime .
este inversabil daca si numai
daca x si n sunt relativ prime .
Demonstratie. Observam mai intai ca daca x
si n sunt relativ prime si y =
x + kn , k I Zn , atunci z si n
sunt de asemenea relativ prime. Daca 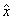 este inversabila in Z n atunci
exista
este inversabila in Z n atunci
exista 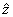 I Z n astfel incat
I Z n astfel incat 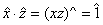 , de unde xz = 1 + kn , pentru un anumit k I Z . Din relatia
, de unde xz = 1 + kn , pentru un anumit k I Z . Din relatia
xz - kn = 1
rezulta ca divizorii comuni ai lui x si n
sunt 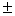 1 , deci x si n sunt relativ prime .
Reciproc , daca x si n sunt relativ prime , atunci exista
numerele intregi a si b astfel incat ax + bn = 1 .Luand imaginile acestor elemente prin surjectia
canonica jn si tinand
seama ca jn (n) = 0 rezulta
1 , deci x si n sunt relativ prime .
Reciproc , daca x si n sunt relativ prime , atunci exista
numerele intregi a si b astfel incat ax + bn = 1 .Luand imaginile acestor elemente prin surjectia
canonica jn si tinand
seama ca jn (n) = 0 rezulta 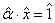 , adica
, adica 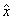 este inversabila in Zn .
este inversabila in Zn .
Conform teoremei precedente , de
exemplu , in Z15 , 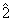 si
si 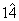 sunt inversabile , dar
sunt inversabile , dar 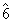 nu este inversabila .
nu este inversabila .
Consecinta . Daca n este numar prim , atunci Zn este corp .
Intr-adevar daca n este numar prim , atunci 1, 2, . . n - 1 sunt relativ prime cu n si deci toate elementele
inelului Zn diferite de elementul neutru al adunarii (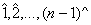 ) sunt inversabile .
) sunt inversabile .
2. Consecinta . Inelul Zn (n > 1) contine atatea
elemente inversabile cate numere naturale mai mici ca n si prime cu n
exista , adica j (n) elemente , unde j : N N este functia lui Euler .
3. Observatie . Legatura dintre elementele inversabile
din Zn si j (n) ne permite sa
dam o noua demonstratie faptului ca indicatorul lui Euler
este o functie multiplicativa . Pentru aceasta vom demonstra lema
care urmeaza .
1.
Lema . Daca m1 si m2 ,
sunt numere intregi relativ prime , atunci 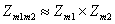 .
.
Demonstratie .
Consideram functia f : Z Zm1 x Zm2 , definita prin f (x) = (j1(x ) , j2 (x)) , unde j j2 sunt surjectiile canonice ale lui Z pe Zm1 , Zm2 . Se
verifica imediat ca f este morfism de inele . Daca x I Ker f , atunci m1 x , m2 x , si deoarece m1 , m2 sunt relativ prime , deducem m1m2 x . Daca m1m2 x , atunci x I Ker f . Deci Ker f = m1m2
Z . Conform teoremei fundamentale de izomorfism Im f Z Ker f = Zm1m2 . Deoarece
Im f are m1m2 elemente rezulta
ca Im f = Zm1 x Zm2 , de unde izomorfismul din enunt .
Aplicand propozitiile din 5. pentru izomorfismul din lema precedenta
se obtine U(Zm1m2) u (Zm1) x U (Zm2) din
care deducem ca j( m1m2 ) = j(m1) j(m2)

