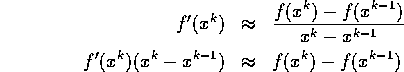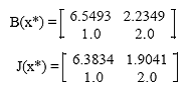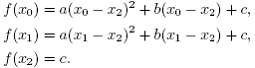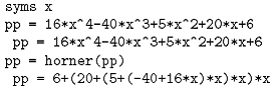Ecuatii neliniare Metoda Broyden Cand derivatele nu pot fi folosite sau sunt prea complicate de calculate, matricea Bk poate fi o aproximare finite a matricii Jacobiane sau o matrice generate de metoda Broyden.
Metoda Broyden
este o generalizare a metodei secantei folosita la rezolvarea sistemelor non-lineare. Metoda secantei inlocuieste derivate cu o diferenta finite:
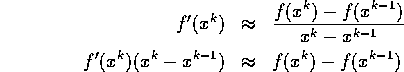 In timp ce metoda Broyden generalizeaza sistemul astfel:
In timp ce metoda Broyden generalizeaza sistemul astfel:  In loc sa foloseasca matricea Jacobiana, Broyden foloseste matricea
In loc sa foloseasca matricea Jacobiana, Broyden foloseste matricea  ce satisface aceasi formula. Observam ca sistemul ne da doar N ecuatii pentru a determina o matrice de forma NXN. Cea mai buna solutie pentru
ce satisface aceasi formula. Observam ca sistemul ne da doar N ecuatii pentru a determina o matrice de forma NXN. Cea mai buna solutie pentru  este o modificare minimala pentru
este o modificare minimala pentru 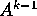 ,
, 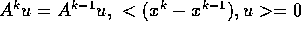 Astfel ajungem la o matrice unic definita.
Astfel ajungem la o matrice unic definita. 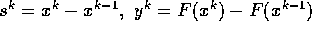 Atunci:
Atunci: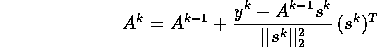 Metoda Broyden ne spune:
Metoda Broyden ne spune: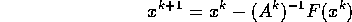 Ar trebui sa calculam din nou matricea inversa, dar pentru a evita calcule inutile putem rezolva
Ar trebui sa calculam din nou matricea inversa, dar pentru a evita calcule inutile putem rezolva 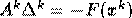 iar apoi inlocuim in
iar apoi inlocuim in 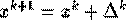 Broyden a sugerat folosirea formulei Sherman-Morrison care ne ajuta sa calcum inversa intr-o maniera eficienta. Din formula aflam: pentru o matrice nonsingulara A si vectorii u,v (astfel incat
Broyden a sugerat folosirea formulei Sherman-Morrison care ne ajuta sa calcum inversa intr-o maniera eficienta. Din formula aflam: pentru o matrice nonsingulara A si vectorii u,v (astfel incat 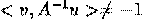 ) atunci:
) atunci: 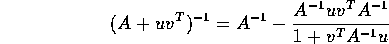 Pentru a implementa formula Sherman-Morrison in Broyden atunci folosim :
Pentru a implementa formula Sherman-Morrison in Broyden atunci folosim :  . Metoda lui Broyden nu este la fel de rapida ca Metoda Newton dar sunt necesare mai putine operatii pe repetitie.
. Metoda lui Broyden nu este la fel de rapida ca Metoda Newton dar sunt necesare mai putine operatii pe repetitie.
Folositi metoda broyden pentru a calcula urmatorul sistem de
ecuatii:
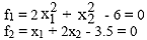
Repetitiile Newton si Broyden sunt date de:
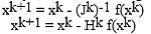
iar matricea Jacobiana si inversa
sunt date de:

Incepand de la 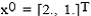 obtinem
urmatoarele valori pentru
obtinem
urmatoarele valori pentru 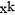 .
Probelma converge dupa trei repetitii cu solutiile x1=1.59586 si x2=0.95206. Deoarece pornim destul de aproape de solutie,
.
Probelma converge dupa trei repetitii cu solutiile x1=1.59586 si x2=0.95206. Deoarece pornim destul de aproape de solutie, 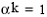 pentru toate repetitiile.
pentru toate repetitiile.

Dar folosind metoda Broyden incepand cu 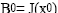 avem:
avem:
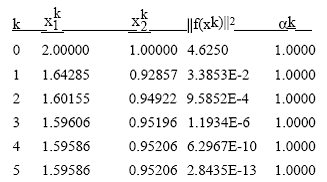
In timp ce ecuatiile sunt rezolvate
exact, matricea Broyden este cam diferita:
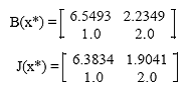 Codul Matlab: function [x] = Broyden(x0,f,dx,n,tol,I) x = zeros(n,1); fx = zeros(n,1); x(:,1) = x0; A = feval(dx,x(:,1)); fx(:,1) = feval(f,x(:,1)); B = inv(A); for i=1:I x(:,i+1) = x(:,i)-B*fx(:,i); fx(:,i+1) = feval(f,(x(:,i+1))); if norm(fx(:,i+1)-fx(:,i))<tol end; y=fx(:,i+1)-fx(:,i); s=x(:,i+1)-x(:,i); oldB=B; B = oldB + (1/(s'*oldB*y))*(s-oldB*y)*s'*oldB; end Metoda Muller
Codul Matlab: function [x] = Broyden(x0,f,dx,n,tol,I) x = zeros(n,1); fx = zeros(n,1); x(:,1) = x0; A = feval(dx,x(:,1)); fx(:,1) = feval(f,x(:,1)); B = inv(A); for i=1:I x(:,i+1) = x(:,i)-B*fx(:,i); fx(:,i+1) = feval(f,(x(:,i+1))); if norm(fx(:,i+1)-fx(:,i))<tol end; y=fx(:,i+1)-fx(:,i); s=x(:,i+1)-x(:,i); oldB=B; B = oldB + (1/(s'*oldB*y))*(s-oldB*y)*s'*oldB; end Metoda Muller
Metoda Muller
foloseste trei puncte la fiecare pas. Aceasa metoda este
folosita pentru a determina polinomul quadric care trece prin aceste trei
puncte si apoi calculeaza radacinile acestui polinom (una din radacini este
folosita pentru a inlocui unul din punctele initiale).
f(x)=0

Metoda este
rapida dar poate genera erori. Daca puntele initiale sunt
foarte apropiate (sau se afla pe o linie dreapta) coeficientii polinomului
determinat pot fi gresiti (si desigur si radacinile vor fi gresite). Iar codul pentru metoda Muller poate fi si el destul de complicat.
O
caracteristica ciudata a acestei metode este
posibilitatea ca polinomul sa nu aiba nicio o radacina reala. Dar in acest caz
poate fi acceptabil sa calculam una din radacinile
complexe.
Coeficientii
a,b si c ce definesc parabola sunt obtinuti calculand
sistemul liniar:
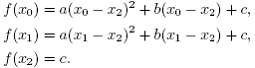
Obtinem imediat :

Obtinem a,b din sistemul liniar:
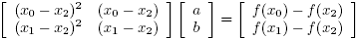
Apoi punem:

si calculam x3-x2:

Pentru a gasi un x3 mai aproape de x2 :

Metoda Muller converge aproximativ catre o radacina simpla
sau dubla. Nu poate converge catre o radacina tripla.
Exemplu:
Gasiti cele patru radacini ale polinomului:

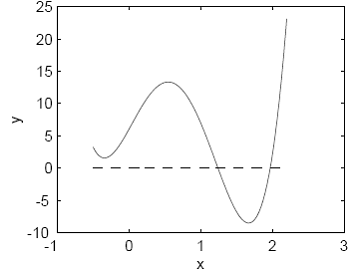
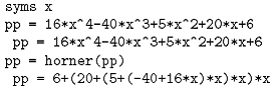
Polinomul este evaluat de functia
Matlab:
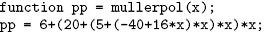
Metoda Muller obtine x3 in functie de valorile date:

Metoda este repetata pana cand
converge. Cele patru radacini sunt:

Cele doua radacini reale pot fi obtinute folosing Metoda
Muller cu valorile initiale [0.5 ,.5] si
[2.5,2.0,2.25].
Programul Principal % Gasirea radacinilor folosind metoda MULLER . function Muller (Poly, x1,x2,x3,A, B,Tol,itmax) fprintf(' Metoda MULLER.n'); format short e % Introducerea datelor disp( Introducerea datelor ');
disp( x1 x2 x3 Tol itmax');
disp( [x1,x2,x3,Tol, itmax] ); % Graficul functiei pentru care se cauta radacini step=(B-A)/100; x=A:step:B; y=feval(Poly,x); plot(x,y) xlabel('x'); ylabel('f(x)'); grid on % ** ** ************ Programul principal ** ** ******* it=0; while it < itmax
it = it + 1;
h1=x1-x2; h2=x2-x3; h3=x1-x3; Px1=feval(Poly,x1); Px2=feval(Poly,x2); Px3=feval(Poly,x3); delta2=Px2-Px3; delta3=Px1-Px3; den=h3*h2*h1; a h2*delta3-h3*delta2)/den; b h3^2*delta2-h2^2*delta3)/den; c=Px3; % disp( ' a b c'); % disp([a,b,c]); D=sqrt(b^2-4*a*c); if abs(b-D)<abs(b+D),
E=b+D;
else E=b-D;
end h=-2*Px3/E;
root=x3+h; disp( ' Iter Aprox-root Error P(root)') disp([it,root,abs(h),feval(Poly,root)]); if abs(h)==0 | feval(Poly,root)==0 disp('Solutia exacta'); disp([it,root]); return end if abs(h) <Tol disp('Solutia aproximativa');
disp([it, root]); return end x1=x2; x2=x3; x3=root; end disp(' Sunt necesare mai multe date(sau repetitii)' );
Program Auxiliar
% TestMuller clear all; A= -10; B=10; x1 x2 x3 Tol=10.^(-10); itmax= Muller('Poly', x1,x2,x3,A, B,Tol,itmax);
Functiile
folosite:
function y=Poly(x) %y= 16*x.^4-40*x.^3+5*x.^2+20*x+6; %y = x.^3 - 4.*x.^2 + 5.*x -2; %y=x.^3 - 4.*x.^2 + 5.*x -2; %y=x^2-3*x-1; %y = x.^3 - 5.*x.^2 + 100.* x - 500.; %y = x.^3 - 5.*x.^2 + x - 5.; %y = x.^3 - 7.*x.^2 + 11.*x - 5; %y=x.^5 + 11.*x.^4 - 21.*x.^3 - 10.*x.^2 -21.*x - 5;
Metoda Atiken Am observat ca metoda lui
Newton converge spre mai multe radacini. Pentru a accelera procesul de convergenta putem folosi metoda
Atiken 
.
Se da secventa

si se defineste diferenta
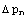
astfel:
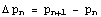 pt n=1,2,3.. Puterile majore ale
pt n=1,2,3.. Puterile majore ale  sunt definite recursiv de:
sunt definite recursiv de: 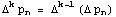 pentru
pentru 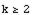 Cand k=2 avem formula
Cand k=2 avem formula 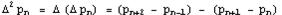 . Care poate fi simplificata:
. Care poate fi simplificata: 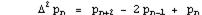 Accelerarea Steffenson Cand metoda Atiken este combinata cu metoda Newton rezulta accelerarea Steffenson. Pornind cu
Accelerarea Steffenson Cand metoda Atiken este combinata cu metoda Newton rezulta accelerarea Steffenson. Pornind cu 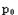 , doi pasi ai metodei sunt folositi pentru a calcula:
, doi pasi ai metodei sunt folositi pentru a calcula: 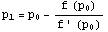 si
si 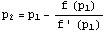 atunci Metoda Atiken
atunci Metoda Atiken 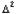 este folosita pentru a calcula
este folosita pentru a calcula 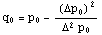 . Pentru a continua setul recursiv punem
. Pentru a continua setul recursiv punem 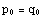 si repetam pasii.
si repetam pasii.
Codul Matlab
(Steffenson)
clear % Generarea unei secvente dintr-o functie repetitiva itmax=input('itmax='); p1=input('p1='); p2=feval('gnn',p1); p3=feval('gnn',p2); % Generarea unei secvente Steffensen for l=1:itmax pa(l)=p1-(p2-p1)^2/(p3-2*p2+p1);
p1=
pa(l);
p2=feval('gnn',p1); p3=
feval('gnn',p2);
end disp(pa'); Functiile folosite: function y=gnn(x) %y=2.^(-x); y= (10/(x+4)).^(1/2); Metoda Newton: Pentru a calcula radacinile F(x 0 putem generaliza metoda lui
Newton scriind:
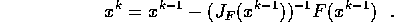
In loc
sa calculam inversa Jacobiana a formulei de mai sus putem parcurge urmatorii pasi:
Definim 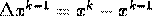 .Apoi:
.Apoi:  Exista doua posibile dificultati cu metoda expusa mai devreme.
Exista doua posibile dificultati cu metoda expusa mai devreme. In primul rand avem de calculat sau evaluat o Jacobiana la fiecare repetitie dar si
un sistem liniar de rezolvat. In al doilea rand stim din experienta ca uneori metoda
Newton e prea mare pentru controlarea erorilor.
Sunt cateva mici modificari
ce pot fi facute sistemului expus.
In primul rand putem evalua valorile fct Jacobiene dupa mai multe repetari. Asa putem reduce numarul de calcule. In al doilea rand putem folosi:
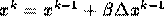
unde
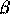 este
este folosit pentru a minimaliza
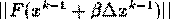
Program Principal:
% Metoda Newton folosita intr-o subrutina. % Folositi acest program impreuna cu cel auxiliar % numit TestNewt . % Also, the functions 'fn' and 'fnprima' are on my website. function Newt (ft,fnprima,Tol,itmax, A, B,p0) format short e % ** ** ******** Introducerea datelor ** ** **********. disp( Introduceti datele ');
disp( A B TOL itmax po ');
disp( [A,B,Tol, itmax,p0] ); %********Graficul functiei pentru care se cauta radacini ** ** % Partition of the interval x used to obtain the graph of f(x). step=(B-A)/100; x1=A:step:B; y1=feval(ft,x1); plot(x1,y1) xlabel('x'); ylabel('f(x)'); grid on % ** ** **Aproximarea Matlab a radaciniilor ** ** ***** MATLABApprox=fzero(ft,p0); format long e; disp('MATLAB Approx.'); disp(MATLABApprox); %***** Se verifica daca exista radacini in intervalul selectat ******* format short e; flag=0; if feval(ft,A)*feval(ft,B)>0 disp('Nu exista radacini in intervalul selectat'); disp(' Alegeti valori noi pentru primele doua aproximari');
return end if feval(ft,A)==0 disp('Punctul terminal din stanga este radacina exacta');
fprintf('Exact root = %fn',A); flag=1;
elseif feval(ft,B)==0 disp(' Punctul terminal din dreapta este radacina exacta'); fprintf('Exact root = %fn',B); flag=1; end % ** ** **********Programul Principal ** ** ********** disp(' it approx. ErrBound f(pn) AbsErr '); it= while it<itmax it=it+1;
pn = p0 - feval(ft,p0)/feval(fnprima,p0); ErrBound=abs(pn-p0); AbsErr=abs(MATLABApprox-pn); disp([it,pn,ErrBound,feval(ft,pn),AbsErr]); if feval(ft,pn)==0 disp('pn este o radacina exacta');
disp('radacina exact si numarul repetitiilor'); format long e; disp([pn,it]); return end % STOP CRITERIA (Se compara doua aproximari consecutive) if ErrBound < Tol disp('radacina aproximata si numarul repetitiilor'); format long e; disp([pn,it]); return else p0=pn;
end end disp('este nevoie de mai multe repetitii');
Programul Auxiliar
% Metoda Newton clear % Toleranta Tol=10^(-20); %Numarul maxim de repetitii itmax= % Intervalul pentru care se creaza graficul A=1; B=3; % Estimarea initiala a radacinii p0=2.; %folosirea subrutinelor Newt('fn','fnprima',Tol,itmax, A, B,p0); % NewtProbl7('fn','fnprima',Tol,itmax, A, B,p0); % NewtProbl26('fn','fnprima',Tol,itmax, A, B,p0); % NewtProbl26b('fn','fnprima',Tol,itmax, A, B,p0); % NewtProbl26c('fn','fnprima',Tol,itmax, A, B,p0);
Functiile
folosite:
function y=fn(x) %y= x.*(x.*x + 4.*x) - 10; %y= x.*(x.*(230.*x.*x + 18.*x+9)-221) -9; %y = exp(x) - x - 1; %y = exp(6*x) + 3*log(2)^2*exp(2*x)-exp(4*x)*log(8) -log(2)^3; %y=x.^2-3.*x+9/4; %y = exp(x) - 3*x.^2; %y = cos(x) - x; %y= x.^2-6; %y = tan(pi*x)-6; y= x.*(1. + x.*(-2.+x)) - 3;
Exemplu:
Considerarti problema gasirii x*,
solutia ecuatiei: f(x 0 pentru x in [a,b]. Presupunem
ca f'(x) este continuu si f'(x 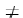 0
pentru x in (a,b).
0
pentru x in (a,b).
Metoda lui Newton:
Algoritm:
Derivare: Fie x0 in [a,b]. Ne
aducem aminte ca liniarizarea 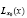 a lui f(x) in punctul (x0,f(x0))
este o functie liniara de forma:
a lui f(x) in punctul (x0,f(x0))
este o functie liniara de forma:
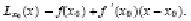
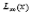 este o aproximare
liniara a lui f(x) aproape de x0. Avand in vedere ca nu putem calcula exact f(x 0 calculam
este o aproximare
liniara a lui f(x) aproape de x0. Avand in vedere ca nu putem calcula exact f(x 0 calculam 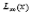 =0.
Acum trebuie sa gasim x1 astfel incat
=0.
Acum trebuie sa gasim x1 astfel incat 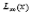 =0.
=0.
 si
si 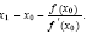
Daca x0 nu este solutie atunci continuam procesul calculand
x2,x3.
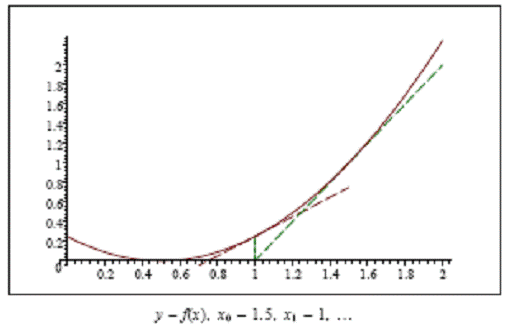
Aplicatii:
1. Aproximati 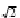 pentru
a gasi solutia ecuatiei
pentru
a gasi solutia ecuatiei 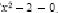 pentru
x>0 cu o precizie de
pentru
x>0 cu o precizie de 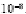
Fie x0=1. Folositi programul newton.m
pentru a calcula aproximarea.
>>[xsol,flag,ct]=newton(1,10^(-8),100)
xsol=
1.00000000000000
1.50000000000000
1.41666666666667
1.41421568627451
1.41421356237469
flag=1
ct=5
Aplicatia 2
Gasiti aproximarea solutiei ecuatiei 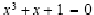 pentru x in [-1 ] cu
precizie de
pentru x in [-1 ] cu
precizie de 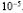 .
.
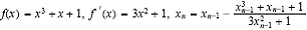
>>[xsol,flag,ct]=newton(-1,10^(-5),100)
xsol =
-1.00000000000000
-0.75000000000000
-0.68604651162791
-0.68233958259731
-0.68232780394651
flag =1
ct =5
Metoda Graffe Metoda Graffe
este o metoda pentru a calcula radacini ale ploinoamelor cu o singura variabila. Aceasta
metoda ,insa, are cateva dificultati. De exemplu: se poate ajunge la exponenti care trec peste valoarea maxima admisa de Matlab sau se poate trece de la polinoame simple la unele complicate si greu de calculat.
Metoda incepe prin a amplifica un polinom p(x) cu
p(-x):
p x) = (x − x1)(x − x2)(x − xn) p − x) = ( − 1)n(x + x1)(x + x2)(x + xn) Astfel reiese: 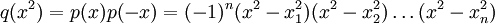
Radacinile lui
q(x2) (privit ca un polinom cu variabila x2)
sunt 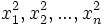
.
Avem radacini patrate ale polinomului p(x). Repetand aceasta procedura de cateva ori se separa radacinile in functie de putere. Repetand operatiunea de k ori rezulta
un polinom cu variabila
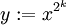
la puterea n.
qk(y) = yn + a1yn − 1 + + an
cu radacinile y1,y2,,yn. Folosind formulele lui Viete rezulta:
a1 = − (y1 + y2 + + yn)
a2 = y1y2 + y1y3 + + yn − 1yn
an = ( − 1)n(y1y2yn)
Astfel vor rezulta radacinile:
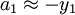
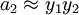 si asa mai departe.
si asa mai departe.
In final sunt
folositi logaritmi pentru a gasi radacinile polinomului original. Metoda
lui Graffe functioneaza cel mai bine pentru polinoame cu radacini unice reale,
desi poate fi adapta si pentru radacini complexe si/sau duble.
Cod Matlab:
function xvector = Broyden(F, J, x0, max_it, tol) % Aceasta functie calculeaza aproximarea pana la zero a lui F % folosind metoda Broyden % Intrari: % F - o functie (posibil multi-dimensionala) % J - F Jacobian % x0 - valoarea initiala % max_it - numarul maxim de repetitii % tol - toleranta % Iesiri: % xvector - vector al lui F xvector = Broyden(F, J, x0, max_it, tol) k = 1; A = J(x0); xvector = x0 - A^-1 * F(x0); s = xvector - x0; y = F(xvector) - F(x0); A = A + ((y - A*s)/norm(s,inf)^2 )*s' ; Ainv = A^-1; % Ainv este inversa lui A; A nu trebuie calculat la fiecare pas while k < max_it Ainv = Ainv + ((s - Ainv*y)*s' * Ainv ) / (s'*Ainv *y); x0 = xvector; % Salveaza xvector pentru a testa convergenta xvector = xvector - Ainv * F(xvector); y = F(xvector) - F(x0); s = xvector - x0; if norm(s, inf) < tol return end k = k+1; end disp('Numarul maxim de repetitii . Metoda a esuat'); xvector = NaN; return