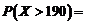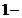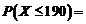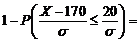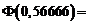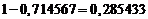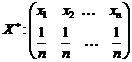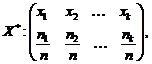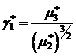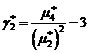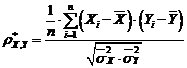Elemente de statistica matematica

Elemente de statistica matematica

Populatie. Selectie. Momente de selectie.

O cercetare statistica porneste de la o colectivitate (sau populatie) alcatuita din elemente (numite unitati) care au o caracteristica generala comuna. Vom presupune ca aceasta caracteristica este descrisa de o variabila aleatoare X.

Se numeste selectie sau esantion o colectivitate partiala finita formata din elemente alese la intamplare. Numarul acestor elemente se numeste volumul selectiei. Selectia este repetata daca elementul ales la intamplare este reintrodus in colectivitatea generala inaintea efectuarii urmatoarei alegeri si este nerepetata daca elementele alese nu se mai introduc in colectivitatea generala.

Vom nota cu 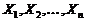valorile observate ale variabilei aleatoare X si le vom numi date (sau valori) de selectie. Privite apriori, in cazul unei selectii repetate, ele sunt variabile aleatoare independente, identic repartizate cu variabila aleatoare X (se numesc variabile de selectie). Cand volumul colectivitatii generale este suficient de mare (comparat cu volumul selectiei), deosebirea dintre o selectie repetata si una nerepetata este nesemnificativa.

Definitie. Orice functie de datele de selectie se numeste functie de selectie sau statistica.

Sa consideram ca valorile de selectie sunt aranjate in ordine crescatoare : 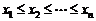Daca sunt distincte, atunci construim variabila aleatoare 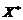(numita variabila aleatoare de selectie) : 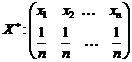Functia de repartitie a acestei variabile se numeste functia de repartitie empirica (sau functia de repartitie de selectie) si o vom nota cu 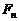. Avem 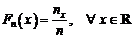, unde 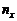reprezinta numarul valorilor de selectie mai mici decat x. Daca valorile de selectie nu sunt distincte, atunci notand cu 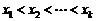valorile de selectie distincte, ordonate crescator, avem : 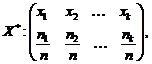unde 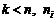este numarul valorilor de selectie egale cu 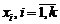si 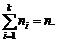Fie F functia de repartitie a lui X (numita si functia de repartitie teoretica).

Teorema lui Glivenko (teorema fundamentala a statisticii matematice).

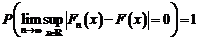
adica, supremul diferentei absolute dintre functia de repartitie empirica si functia de repartitie teoretica converge aproape sigur la zero.

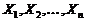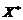Definitii. Fie selectia . Momentele variabilei aleatoare de selectie se numesc momente de selectie (sau momente empirice). Numim moment initial de selectie de ordin r variabila aleatoare

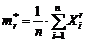
In cazul particular 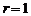, el se numeste media de selectie si se noteaza cu 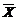(sau cu 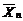), deci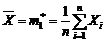

Numim moment centrat de selectie de ordin r variabila aleatoare

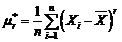
Pentru 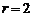el se numeste dispersia de selectie (se mai noteaza cu 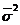sau cu 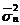), deci 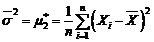. Avem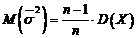

Numim dispersia de selectie modificata (sau corectata) variabila aleatoare 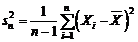. Avem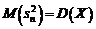

Propozitia 1. Cand momentul teoretic de ordin r (notat 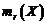) exista, avem : 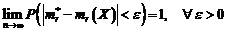adica, momentele initiale de selectie converg in probabilitate catre momentele initiale teoretice de acelasi ordin.

Propozitia 2. Avem 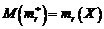, adica, media momentului initial de selectie de ordin r este egala cu momentul initial de ordin r al variabilei aleatoare X.

Cu ajutorul momentelor de selectie definim si alti indicatori de selectie :

asimetria de selectie (sau asimetria empirica) :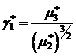

excesul de selectie (sau excesul empiric) :

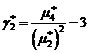
coeficientul de corelatie de selectie (sau coeficientul de corelatie empiric) :

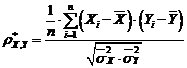
Propozitia 3 (Selectia din populatia normala).

Daca X are repartitia normala 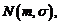atunci:

a) media de selectie 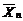are repartitia normala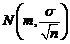

b) variabilele aleatoare 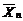si 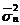(media de selectie si dispersia de selectie) sunt independente.

1). La o statie meteorologica temperaturile (in grade Celsius) inregistrate in ultimii 8 ani, la ora 12 din data de 1 august, au fost : 30, 24, 35, 36, 32, 23, 31, 37. Sa se scrie functia de repartitie empirica si sa se calculeze media de selectie (temperatura medie multianuala a locului), dispersia de selectie si dispersia de selectie modificata.

Rezolvare. Avem :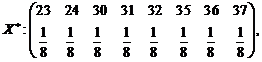

,

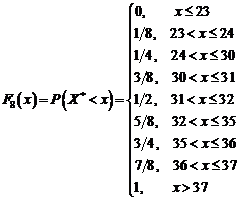
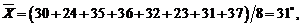
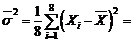
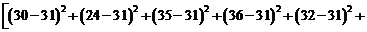
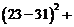
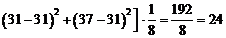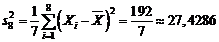
2). Se considera o colectivitate de oameni a caror inaltime are repartitia normala cu media 170 cm. Probabilitatea ca media de selectie corespunzatoare unei selectii de volum 36 sa depaseasca 175 cm este 0,1977. Sa se determine probabilitatea ca luand la intamplare un membru al colectivitatii, el sa aiba inaltimea peste 190 cm.

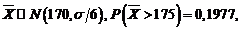
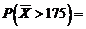
Rezolvare Avem 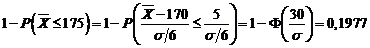, unde 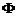este functia de repartitie a normalei 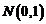. Rezulta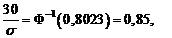 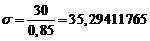, probabilitatea ceruta este