Introduction to Predictive Modeling: Regressions
Regressions
offer a different approach to prediction compared to decision trees.
Regressions, as parametric models, assume a specific association structure
between inputs and target. By contrast, trees, as predictive algorithms, do not
assume any association structure; they simply seek to isolate concentrations of
cases with like-valued target measurements.
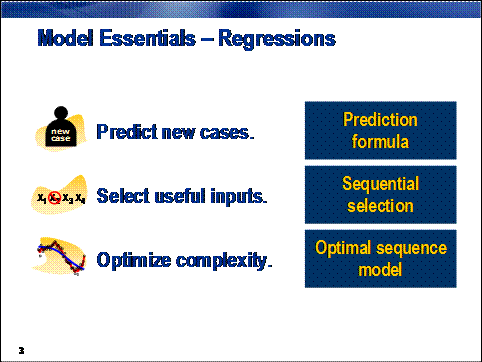
The
regression approach to the model essentials in SAS Enterprise Miner is outlined
over the following pages. Cases are scored using a simple mathematical prediction formula. One of several
heuristic sequential selection
techniques is used to pick from a collection of possible inputs and creates a
series of models with increasing complexity. Fit statistics calculated from
validation data select the optimal
sequence model.
Regressions predict cases using a mathematical
equation involving values of the input variables.

In standard
linear regression, a prediction estimate for the target variable is formed from
a simple linear combination of the inputs. The intercept centers the range of
predictions, and the remaining parameter estimates determine the trend strength
(or slope) between each input and the target. The simple structure of the model
forces changes in predicted values to occur in only a single direction (a
vector in the space of inputs with elements equal to the parameter estimates).
Intercept and parameter
estimates are chosen to minimize the
squared error between the predicted and observed target values (least squares
estimation). The prediction estimates can be viewed as a linear approximation
to the expected (average) value of a target conditioned on observed input
values.
Linear
regressions are usually deployed for targets with an interval measurement
scale.

Logistic regressions are closely related to linear regressions.
In logistic regression, the expected value of the target is transformed by a link function to restrict its value to the
unit interval. In this way, model predictions can be viewed as primary outcome
probabilities. A linear combination of the inputs generates a logit score, the log of the odds of
primary outcome, in contrast to the linear regression's direct prediction of
the target.
The presence of
the link function complicates parameter estimation. Least squares estimation is
abandoned in favor of maximum likelihood estimation. The likelihood function is
the joint probability density of the data treated as a function of the
parameters. The maximum likelihood estimates the values of the parameters that
maximize the probability of obtaining the training sample.
If your interest is ranking predictions,
linear and logistic regressions will yield virtually identical results.

For binary prediction, any monotonic function that
maps the unit interval to the real number line can be considered as a link. The
logit link function is one of the
most common. Its popularity is due, in part, to the interpretability of the
model.
There are two equivalent ways to interpret a
logistic regression model. Both relate changes in input measurements to changes
in odds of primary outcome.
An
odds ratio expresses the increase in primary
outcome odds associated with a unit change in an input. It is obtained by
exponentiating the parameter estimate of the input of interest.
A
doubling amount gives the amount of change required for doubling the primary
outcome odds. It is equal to log(2) ≈ 0.69 divided by the parameter
estimate of the input of interest.
If the predicted logit scores remain in
the range -2 to +2, linear and logistic regression models of binary targets are
virtually indistinguishable. Balanced
sampling (Chapter 7) often ensures this. Thus, the prevalence of balanced
sampling in predictive modeling might, in fact, be a vestigial practice from a
time when maximum likelihood estimation was computationally extravagant.

To demonstrate the properties of a logistic
regression model, consider the two-color prediction problem introduced in
Chapter 3. As before, the goal is to predict the target color, based on
location in the unit square.
The predictions can be decisions, rankings, or
estimates. The logit equation produces a ranking or logit score. To get a
decision, you need a threshold. The easiest way to get a meaningful threshold
is to convert the prediction ranking to a prediction estimate. You can obtain a
prediction estimate using a straightforward transformation of the logit score,
the logistic function. The logistic
function is simply the inverse of the logit function.

Parameter estimates are obtained by maximum
likelihood estimation. These estimates can be used in the logit and logistic
equations to obtain predictions. The plot on the right shows the prediction
estimates from the logistic equation. One of the attractions of a standard
logistic regression model is the simplicity of its predictions. The contours
are simple straight lines. (In higher dimensions, they would be hyperplanes.)
This enables a straightforward interpretation of the model using the odds
ratios and doubling amounts shown at the bottom left. Unfortunately, simplicity
can also lead to prediction bias (as scrutiny of the prediction contours
suggests).
The
last section of this chapter shows a way to extend the capabilities of logistic
regression to address this possible bias.

To score a new
case, the values of the inputs are plugged into the logit or logistic equation.

This action creates
a logit score or prediction estimate. Typically, if the prediction estimate is
greater than 0.5 (or equivalently, the logit score is positive), cases are
usually classified to the primary outcome. (This assumes an equal
misclassification cost. See Chapter 7.)
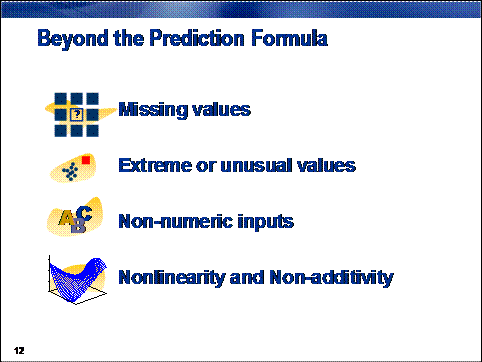
While the prediction formula would seem to be the
final word in scoring a new case with a regression model, there are actually
several additional issues that must be addressed.
What
should be done when one of the input values used in the prediction formula is
missing? You might be tempted to simply treat the missing value as zero and
skip the term involving the missing value. While this approach can generate a
prediction, this prediction is usually biased beyond reason.
How do you score cases with unusual values?
Regression models make their best predictions for cases near the centers of the
input distributions. If an input can have (on rare occasion) extreme or outlying
values, the regression should respond appropriately.
What value should be used in the prediction
formula when the input is not a number? Categorical inputs are common in
predictive modeling. They did not present a problem for the rule-based
predictions of decision trees, but regression predictions come from algebraic
formulas that require numeric inputs. (You cannot multiply marital status by a
number.) A method to include nonnumeric data in regression is needed.
What happens when the relationship between
the inputs and the target (or rather logit of the target) is not a straight
line? It is preferable to be able to build regression models in the presence of
nonlinear (and even non-additive) input target associations.
The above
questions are presented as scoring-related issues. They are also problems for
model construction. (Maximum likelihood estimation requires iteratively scoring
the training data.) The first of these, handling missing values, is dealt with
immediately. The remaining issues are addressed, in turn, at the end of this
chapter.
The default
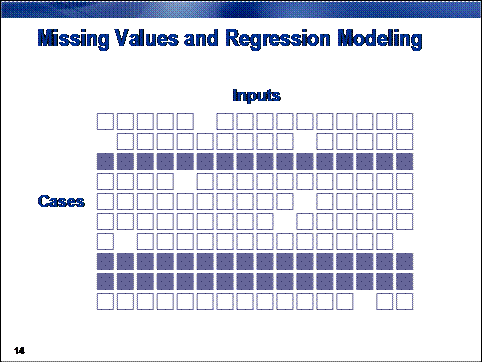
method for treating missing values in most regression tools in SAS Enterprise
Miner is complete-case analysis. In complete-case analysis, only those
cases without any missing values are used in the analysis.
Even a smattering
of missing values can cause an enormous loss of data in high dimensions. For
instance, suppose that each of the k
input variables is missing at random with probability a. In this situation, the expected proportion
of complete cases is as follows:
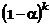
Therefore, a 1%
probability of missing (a=.01) for 100 inputs leaves only 37% of the
data for analysis, 200 leaves 13%, and 400 leaves 2%. If the missingness
were increased to 5% (a=.05), then <1% of the data would be
available with 100 inputs.

The purpose of
predictive modeling is scoring new cases. How would a model built on the
complete cases score a new case if it had a missing value? To decline to score
new incomplete cases would be practical only if there were a very small number
of missing values.

Missing values arise for a variety of
reasons. For example, the time since last donation to a card campaign is
meaningless if someone did not donate to a card campaign. In the PVA97NK data set, several demographic inputs have
missing values in unison. The probable cause was no address match for the
donor. Finally, certain information, such as an individual's total wealth, is
closely guarded and is often not disclosed.

Missing value
replacement strategies fall into one of two categories.
Synthetic distribution methods use a one-size-fits-all approach to
handle missing values. Any case with a missing input measurement has the
missing value replaced with a fixed number. The net effect is to modify an
input's distribution to include a point mass at the selected fixed number. The
location of the point mass in synthetic distribution methods is not arbitrary.
Ideally, it should be chosen to have minimal impact on the magnitude of an
input's association with the target. With many modeling methods, this can be
achieved by locating the point mass at the input's mean value.
Estimation methods eschew the one-size-fits-all approach and
provide tailored imputations for each case with missing values. This is done by
viewing the missing value problem as a prediction problem. That is, you can train
a model to predict an input's value from other inputs. Then, when an input's
value is unknown, you can use this model to predict or estimate the unknown
missing value. This approach is best suited for missing values that result from
a lack of knowledge, that is, no-match or non-disclosure, but it is not
appropriate for not-applicable missing values. (An exercise at the end of this
chapter demonstrates using decision trees to estimate missing values.)
Because
predicted response might be different for cases with a missing input value, a
binary imputation indicator variable is often added to the training data. Adding
this variable enables a model to adjust its predictions in the situation where missingness
itself is correlated with the target.
 Managing Missing Values
Managing Missing Values
The
demonstrations in this chapter assume that you completed the demonstrations in
Section 4.1.
As discussed
above, regression requires that a case have a complete set of input values for
both training and scoring.
Right-click the PVA97NK data source and select Explore . from the menu. The
Explore - AAEM.PVA97NK window
opens.
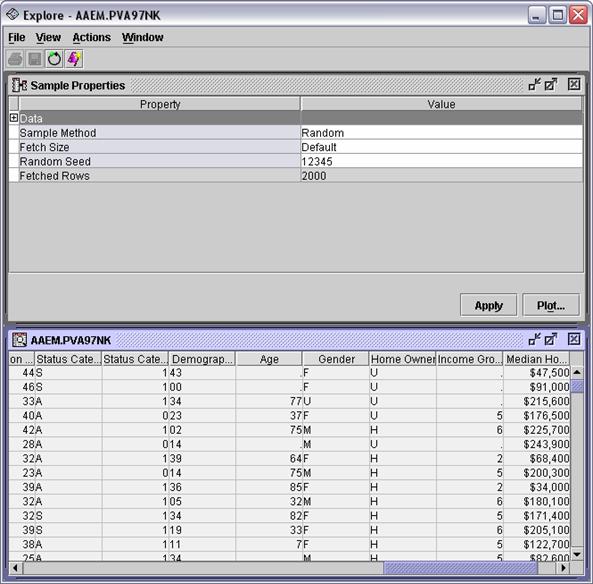
There
are several inputs with a noticeable frequency of missing values, for example, Age and Income Group
There are several ways to proceed:
Do nothing. If there are very few cases with missing values,
this is a viable option. The difficulty with this approach comes when the model
must predict a new case that contains a missing value. Omitting the missing
term from the parametric equation usually produces an extremely biased
prediction.
Impute a synthetic value for the missing value. For
example, if an interval input contains a missing value, replace the missing
value with the mean of the non-missing values for the input. This eliminates
the incomplete case problem but modifies the input's distribution. This can
bias the model predictions.
Making the missing value imputation process
part of the modeling process allays the modified distribution concern. Any
modifications made to the training data are also made to the validation data
and the remainder of the modeling population. A model trained with the modified
training data will not be biased if the same modifications are made to any
other data set that the model might encounter (and the data has a similar
pattern of missing values).
Create a missing
indicator for each input in the data set. Cases often contain missing
values for a reason. If the reason for the missing value is in some way related
to the target variable, useful predictive information is lost.
The missing indicator is 1 when the
corresponding input is missing and 0 otherwise. Each missing indicator becomes
an input to the model. This enables modeling of the association between the
target and a missing value on an input.
To address
missing values in the PVA97NK data set, impute synthetic data values and
create missing value indicators.
Select the Modify tab.
Drag an Impute tool into the diagram
workspace.
Connect the Data
Partition node to the Impute node.

Select the Impute
node and examine the Properties panel.
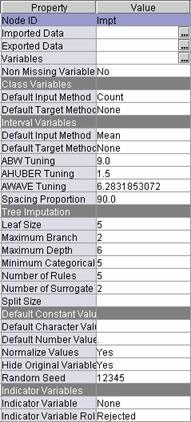
The
defaults of the Impute node are as follows:
For interval inputs, replace any missing
values with the mean of the non-missing value
For categorical inputs, replace any missing
values with the most frequent category.
Select Indicator Variable
Unique.
Select Indicator Variable Role
Input.
With
these settings, each input with missing values generates a new input. The new
input named IMP_original_input_name
will have missing values replaced by a synthetic value and nonmissing values
copied from the original input. In addition, new inputs named M_original_input_name will be added to the
training data to indicate the synthetic data values.
Run the Impute node and review the Results window. Three inputs had
missing values.
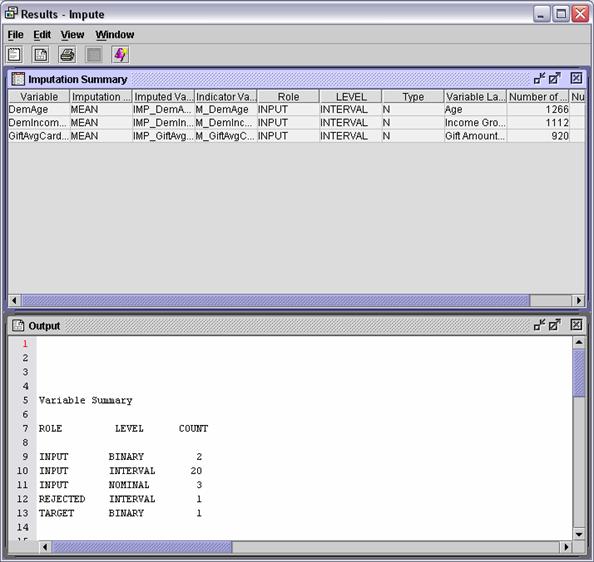
With
all missing values imputed, the entire training data set is available for
building the logistic regression model. In addition, a method is in place for
scoring new cases with missing values. (See Chapter 8.)
 Running the Regression Node
Running the Regression Node
There are several tools in SAS Enterprise Miner to
fit regression or regression-like models. By far, the most commonly used (and,
arguably, the most useful) is the simply named Regression tool.
Select the Model tab.
Drag a Regression tool into the diagram
workspace.
Connect the Impute
node to the Regression node.
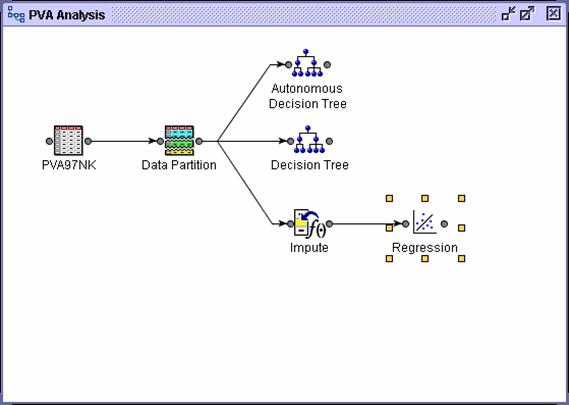
The
Regression node can create several types of regression models, including linear
and logistic. The type of default regression type is determined by the target's
measurement level.
Run the Regression
node and view the results. The Results - Regression window opens.

Maximize the Output
window.
Lines
5-13 of the Output window summarize the roles of variables used (or not) by the
Regression node.
ROLE LEVEL COUNT
INPUT BINARY 5
INPUT INTERVAL 20
INPUT NOMINAL 3
REJECTED INTERVAL 1
TARGET BINARY 1
The
fit model has 28 inputs that predict a binary target.
Lines 45-57 give more information about the model, including the
training data set name, target variable name, number of target categories, and
most importantly, the number of model parameters.
Training Data Set EMWS2.IMPT_TRAIN.VIEW
DMDB Catalog WORK.REG_DMDB
Target Variable TargetB (Target Gift Flag)
Target Measurement Level Ordinal
Number of Target Categories 2
Error MBernoulli
Link Function Logit
Number of Model Parameters 86
Number of Observations 4843
Based on the
introductory material on logistic regression that is presented above, you might
expect to have a number of model parameters equal to the number of input
variables. This ignores the fact that a single nominal input (for example, DemCluster) can generate scores of model parameters.
You can see the number of parameters (or degrees of freedom) that each input
contributes to the model, as well as each input's statistical significance, by
viewing lines 117-146 of the Output window.
The Type 3
Analysis tests the statistical significance of adding the indicated input to a
model that already contains other listed inputs. Roughly speaking, a value near
0 in the Pr > Chi-Square column indicates a significant input; a
value near 1 indicates an extraneous input.
Type 3 Analysis of Effects
Wald
Effect DF Chi-Square Pr > ChiSq
DemCluster
53 44.0996 0.8030
DemGender
2 0.0032 0.9984
DemHomeOwner 1 0.0213 0.8840
DemMedHomeValue
1 9.3921 0.0022
DemPctVeterans
1 0.1334 0.7150
GiftAvg36
1 4.5339 0.0332
GiftAvgAll
1 0.8113 0.3677
GiftAvgLast
1 0.0003 0.9874
GiftCnt36
1 0.6848 0.4079
GiftCntAll
1 0.0144 0.9044
GiftCntCard36
1 2.4447 0.1179
GiftCntCardAll
1 0.0073 0.9320
GiftTimeFirst
1 3.8204 0.0506
GiftTimeLast 1 15.8614 <.0001
IMP_DemAge
1 4.7087 0.0300
IMP_DemIncomeGroup 1 11.1804 0.0008
IMP_GiftAvgCard36 1 0.0758 0.7830
M_DemAge 1 0.3366 0.5618
M_DemIncomeGroup 1 0.0480 0.8266
M_GiftAvgCard36
1 5.4579 0.0195
PromCnt12
1 3.4896 0.0618
PromCnt36
1 4.8168 0.0282
PromCntAll
1 0.2440 0.6214
PromCntCard12
1 0.2867 0.5923
PromCntCard36
1 1.1416 0.2853
PromCntCardAll
1 1.6851 0.1942
StatusCat96NK
5 6.5422 0.2570
StatusCatStarAll 1 2.7676 0.0962
The
statistical significance measures range from <0.0001 (highly significant) to
0.9997 (highly dubious). Results such as this suggest that certain inputs can
be dropped without affecting the predictive prowess of the model.
Restore the
Output window to its original size and maximize the Fit Statistics window.

If
the decision predictions are of interest, model fit can be judged by
misclassification. If estimate predictions are the focus, model fit can be
assessed by average square error. There appears to be some discrepancy between
the values of these two statistics on the train and validation data. This
indicates possible overfit of the model. It can be mitigated by employing an
input selection procedure.

The second task that all predictive models should
perform is input selection. One way to find the optimal set of inputs for a
regression is simply to try every combination. Unfortunately, the number of
models to consider using this approach increases exponentially in the number of
available inputs. Such an exhaustive search is impractical for realistic
prediction problems.
An alternative to the exhaustive search is to restrict the search to a
sequence of improving models. While this might not find the single best model,
it is commonly used to find models with good predictive performance. The
Regression node in SAS Enterprise Miner provides three sequential selection
methods.
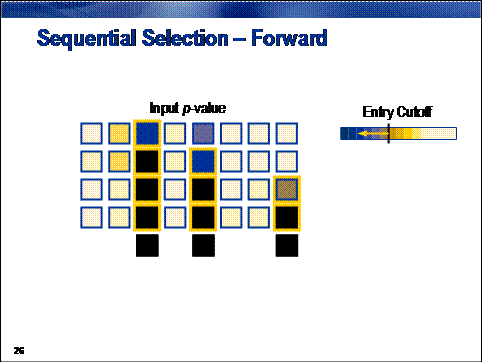
Forward selection creates a
sequence of models of increasing complexity. The sequence starts with the
baseline model, a model predicting the overall average target value for all
cases. The algorithm searches the set of one-input models and selects the model
that most improves upon the baseline model. It then searches the set of
two-input models that contain the input selected in the previous step and
selects the model showing the most significant improvement. By adding a new
input to those selected in the previous step, a nested sequence of increasingly
complex models is generated. The sequence terminates when no significant
improvement can be made.
Improvement is quantified by the usual statistical measure of
significance, the p-value. Adding terms in this nested fashion always
increases a model's overall fit statistic. By calculating the change in the fit
statistic and assuming that the change conforms to a chi-squared distribution,
a significance probability, or p-value,
can be calculated. A large fit statistic change (corresponding to a large
chi-squared value) is unlikely due to chance. Therefore, a small p-value indicates a significant
improvement. When no p-value is below
a predetermined entry cutoff, the
forward selection procedure terminates.

In contrast to forward selection,
backward selection creates a sequence of models of decreasing complexity. The sequence starts with a saturated model, which
is a model that contains all available inputs and, therefore, has the highest
possible fit statistic. Inputs are sequentially removed from the model. At each
step, the input chosen for removal least reduces the overall model fit
statistic. This is equivalent to removing the input with the highest p-value. The sequence terminates when
all remaining inputs have a
p-value in excess of the
predetermined stay cutoff.
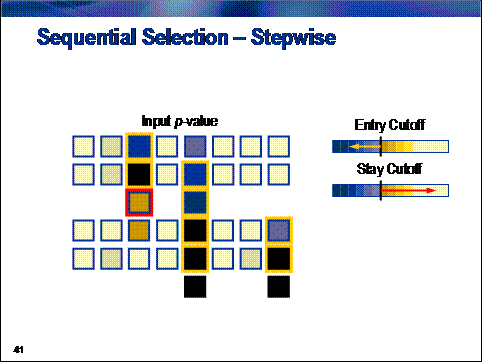
Stepwise selection combines elements from both the forward and backward selection
procedures. The method begins in the same way as the forward procedure,
sequentially adding inputs with the smallest p‑value below the entry cutoff. After each input is added,
however, the algorithm re-evaluates the statistical significance of all
included inputs. If the p-value of
any of the included input exceeds a stay cutoff, the input is removed from the
model and re-entered into the pool of inputs that are available for inclusion
in a subsequent step. The process terminates when all inputs available for
inclusion in the model have p-values
in excess of the entry cutoff and all inputs already included in the model have
p-values below the stay cutoff.
 Selecting Inputs
Selecting Inputs
Implementing a sequential
selection method in the regression node requires a minor change to the
Regression node settings.
Close the Regression results
window.
Select Selection Model Stepwise on the
Regression node property sheet.
The Regression node is now
configured to use stepwise selection to choose inputs for the model.
Run the Regression node and
view the results.
Select the Output tab and scroll to lines
95-121.
The stepwise procedure
starts with Step 0, an intercept-only regression model. The value of the
intercept parameter is chosen so that the model predicts the overall target
mean for every case. The parameter estimate and the training data target
measurements are combined in an objective function. The objective function is
determined by the model form and the error distribution of the target. The
value of the objective function for the intercept-only model is compared to the
values obtained in subsequent steps for more complex models. A large decrease
in the objective function for the more complex model indicates a significantly
better model.
Optimization Results
Iterations 0 Function Calls 3
Hessian Calls 1 Active Constraints 0
Objective Function 3356.9116922 Max Abs Gradient Element 7.225331E-12
Ridge 0 Actual Over Pred Change 0
Convergence criterion (ABSGCONV=0.00001) satisfied.
Likelihood Ratio Test
for Global Null Hypothesis: BETA=0
-2 Log
Likelihood Likelihood
Intercept Intercept & Ratio
Only Covariates Chi-Square DF Pr > ChiSq
6713.823 6713.823 0.0000 0 .
Analysis of Maximum
Likelihood Estimates
Standard Wald Standardized
Parameter DF Estimate Error Chi-Square Pr > ChiSq Estimate Exp(Est)
Intercept 1 -0.00041 0.0287 0.00 0.9885 1.000
Step 1 adds one input to the
intercept-only model. The input and corresponding parameter are chosen to
produce the largest decrease in the objective function. To estimate the values
of the model parameters, the modeling algorithm makes an initial guess for their
values. The initial guess is combined with the training data measurements in
the objective function. Based on statistical theory, the objective function is
assumed to take its minimum value at the correct estimate for the parameters. The
algorithm decides whether changing the values of the initial parameter
estimates can decrease the value of objective function. If so, the parameter
estimates are changed to decrease the value of the objective function and the
process iterates. The algorithm continues iterating until changes in the
parameter estimates fail to substantially decrease the value of the objective
function.
The Step 1 optimization is
summarized in the Output window, lines 121-164.
Step 1: Effect
GiftCntCard36 entered.
The DMREG Procedure
Newton-Raphson Ridge
Optimization
Without Parameter
Scaling
Parameter
Estimates 2
Optimization Start
Active Constraints 0 Objective Function 3356.9116922
Max Abs Gradient Element 118.98162296
Ratio
Between
Actual
Objective Max
Abs and
Function Active Objective Function Gradient Predicted
Iter Restarts Calls Constraints Function Change Element Ridge Change
1 0 2 0 3308 48.5172 2.3587 0 1.014
2 0 3 0 3308 0.0416 0.00805 0 1.002
3 0 4 0 3308 2.979E- 6.214E-8 0 1.000
Optimization Results
Iterations 3 Function Calls 6
Hessian Calls 4 Active Constraints 0
Objective Function 3308.3529331 Max Abs Gradient Element 6.2144229E-8
Ridge
0 Actual Over Pred Change 0.9999995175
Convergence criterion (GCONV=1E-6) satisfied.
The
output next compares the model fit in step 1 with the model fit in step 0. The
objective functions of both models are multiplied by 2 and differenced. The
difference is assumed to have a chi-square distribution with 1 degree of
freedom. The hypothesis that the two models are identical is tested. A large
value for the chi-square statistic makes this hypothesis unlikely.
The
hypothesis test is summarized in lines 167-173.
Likelihood Ratio Test for Global Null Hypothesis: BETA=0
-2 Log Likelihood Likelihood
Intercept Intercept & Ratio
Only Covariates Chi-Square DF Pr > ChiSq
6713.823 6616.706 97.1175 1 <.0001
Next, the output summarizes an analysis of the
statistical significance of individual model effects (lines 176-181). For the
one input model, this is similar to the global significance test above.
Type 3 Analysis of
Effects
Wald
Effect DF Chi-Square Pr > ChiSq
GiftCntCard36
1 93.0507 <.0001
Finally,
an analysis of individual parameter estimates is made. The standardized
estimates and the odds ratios merit special attention.
Analysis
of Maximum Likelihood Estimates
Standard Wald Standardized
Parameter DF Estimate Error Chi-Square Pr > ChiSq Estimate Exp(Est)
Intercept 1 -0.3360 0.0450 55.78 <.0001 0.715
GiftCntCard36 1 0.1841 0.0191 93.05 <.0001 0.1596 1.202
Odds
Ratio Estimates
Point
Effect Estimate
GiftCntCard36 1.202
The standardized estimates
present the effect of the input on the log-odds of donation. The values are
standardized to be independent of the input's unit of measure. This provides a
means of ranking the importance of inputs in the model.
The odds ratio estimates
indicate by what factor the odds of donation increase for each unit change in
the associated input. Combined with knowledge of the range of the input, this
provides an excellent way to judge the practical (as opposed to the
statistical) importance of an input in the model.
The stepwise selection
process continues for seven steps. After the eighth step, neither adding nor
removing inputs from the model significantly changes the model fit statistic. At
this point the Output window provides a summary of the stepwise procedure. The
summary shows the step in which each input was added and the statistical
significance of each input in the final eight-input model (lines 810-825).
NOTE: No (additional) effects met the 0.05 significance
level for entry into the model.
Summary of Stepwise Selection
Effect Number Score Wald
Step Entered DF In Chi-Square Chi-Square Pr > ChiSq
1 GiftCntCard36 1 1 95.6966 <.0001
2 GiftTimeLast 1 2 29.9410 <.0001
3 DemMedHomeValue 1 3 25.5086 <.0001
4 GiftTimeFirst 1 4 15.1942 <.0001
5 GiftAvg36 1 5 13.2369 0.0003
6 IMP_DemIncomeGroup 1 6 13.3458 0.0003
7 M_GiftAvgCard36 1 7 10.0412 0.0015
8 IMP_DemAge 1 8 4.2718 0.0387
The default
selection criterion selects the model from step 8 as the model with optimal
complexity (lines 828-830). As the next section shows, this might not be the
optimal based on the fit statistic that is appropriate for your analysis
objective.
The
selected model, based on the CHOOSE=NONE criterion, is the model trained in
Step 8. It consists of the following effects:
Intercept DemMedHomeValue GiftAvg36 GiftCntCard36 GiftTimeFirst GiftTimeLast IMP_DemAge IMP_DemIncomeGroup M_GiftAvgCard36
For convenience, the output
from step 9 is repeated. An excerpt from the analysis of individual parameter
estimates is shown below (lines 857-870).
Analysis
of Maximum Likelihood Estimates
Standard Wald Standardized
Parameter DF Estimate Error Chi-Square Pr > ChiSq Estimate Exp(Est)
Intercept 1 -0.3363 0.2223 2.29 0.1304 0.714
DemMedHomeValue 1 1.349E-6 3.177E-7 18.03 <.0001 0.0737 1.000
GiftAvg36 1 -0.0131 0.00344 14.59 0.0001 -0.0712 0.987
GiftCntCard36 1 0.1049 0.0242 18.80 <.0001 0.0910 1.111
GiftTimeFirst 1 0.00305 0.000807 14.28 0.0002 0.0631 1.003
GiftTimeLast 1 -0.0376 0.00747 25.32 <.0001 -0.0848 0.963
IMP_DemAge 1 0.00440 0.00213 4.27 0.0389 0.0347 1.004
IMP_DemIncomeGroup 1 0.0758 0.0192 15.55 <.0001 0.0680 1.079
M_GiftAvgCard36 0 1 0.1449 0.0462 9.83 0.0017 1.156
The parameter with the
largest standardized estimate is GiftCntCard36
The odds ratio estimates
show that a unit change in M_GiftAvgCard36 produces the largest change in the donation odds.
Point
Effect Estimate
DemMedHomeValue 1.000
GiftAvg36 0.987
GiftCntCard36 1.111
GiftTimeFirst
1.003
GiftTimeLast 0.963
IMP_DemAge 1.004
IMP_DemIncomeGroup 1.079
M_GiftAvgCard36 0 vs 1 1.336
Restore
the Output window and maximize the Fit Statistics window.
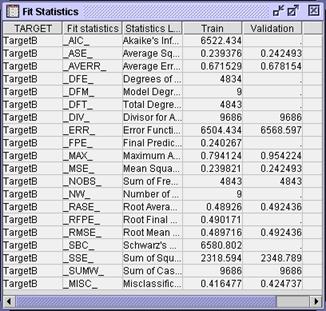
Considering the
analysis from an estimate prediction perspective, the simpler stepwise
selection model, with a lower validation average squared error, is an
improvement over the full model (from the previous section). From a decision
prediction perspective, however, the larger full model, with a slightly lower
misclassification, is preferred.
This somewhat
ambiguous result comes from a lack of complexity optimization, by default, in
the Regression node. This oversight is handled in the next demonstration.

Regression complexity
is optimized by choosing the optimal model in the sequential selection
sequence.
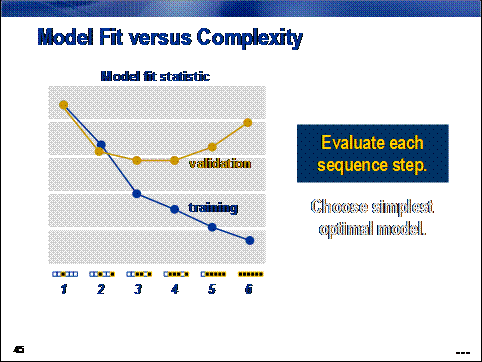
The process
involves two steps. First, fit statistics are calculated for the models
generated in each step of the selection process using both the training and
validation data sets.

Then, as with the
decision tree in Chapter 4, the simplest model (that is, the one with the
fewest inputs) with the optimal fit statistic is selected.
 Optimizing Complexity
Optimizing Complexity
In the same
manner as the decision tree, you can tune a regression model to give optimal
performance on the validation data. The basic idea involves calculating a fit
statistic for each step in the input selection procedure and selecting the step
(and corresponding model) with the optimal fit statistic value. To avoid bias,
of course, the fit statistic should be calculated on the validation data set.
Select View Model
Iteration
Plot. The Iteration Plot window opens.

The
Iteration Plot window shows (by default) the average squared error from the
model selected in each step of the stepwise selection process. Apparently, the
smallest average squared error occurs in step 6, rather than in the final
model, step 8. If your analysis objective requires estimates predictions, the
model from step 6 should provide slightly less biased ones.
Select Select Chart
Misclassification Rate.

The
iteration plot shows that the model with the smallest misclassification rate
occurs in step 4. If your analysis objective requires decision predictions, the
predictions from the step 4 model will be as accurate as the predictions from
the final step 8 model.
The
selection process stopped at step 8 to limit the amount of time spent running
the stepwise selection procedure. In step 8, no more inputs had a chi-squared p-value below 0.05. The value 0.05 is a
somewhat arbitrary holdover from the days of statistical tables. With the
validation data available to gauge overfitting, it is possible to eliminate
this restriction and obtain a richer pool of models to consider.
Close the Results -
Regression window.
Select Use Selection Default
No from the Regression node Properties
panel.
Type in the Entry Significance
Level
field.
Type in the Stay Significance
Level
field.
The
Entry Significance value enables any input into the model. (The one chosen will
have the smallest p-value.) The Stay
Significance value keeps any input in the model with a p-value less than 0.5. This second choice is somewhat arbitrary. A
smaller value can terminate the stepwise selection process earlier, while a
larger value can maintain it longer. A Stay Significance of 1.0 forces stepwise
to behave in the manner of a forward selection.
Run the Regression node and
view the results.
Select View
Model
Iteration
Plot. The Iteration Plot window opens.

The
iteration plot shows the smallest average squared errors occurring in steps 15
or 16.
Select Select Chart Misclassification
Rate.
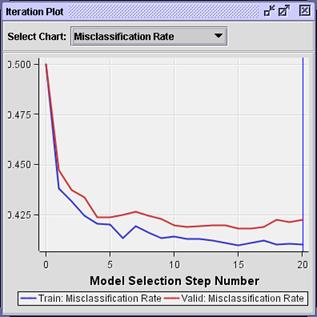
The
iteration plot shows the smallest validation misclassification rates also
occurring near steps 15-16.
You
can configure the Regression node to select the model with the smallest fit
statistic (rather than the final stepwise selection iteration). This method is
how SAS Enterprise Miner optimizes complexity for regression models.
Close the Results -
Regression window.
If your predictions are decisions, use the following setting:
Select Selection
Criterion Validation
Misclassification. (Equivalently, you can select
Validation Profit / Loss. The
equivalence is demonstrated in Chapter 7.)
If your predictions are
estimates (or rankings), use the following setting:
Select Selection
Criterion Validation
Error.
The continuing
demonstration assumes validation error selection criteria.
Run the Regression node and
view the results.
Select View Model
Iteration
Plot.

The
vertical blue line shows the model with the optimal validation average squared
error (step 17).
Select the Output window and view lines 2256-2276.
Analysis of Maximum Likelihood
Estimates
Standard Wald Standardized
Parameter DF Estimate Error Chi-Square Pr > ChiSq Estimate Exp(Est)
Intercept 1 -0.3042 0.2892 1.11 0.2929 0.738
DemMedHomeValue 1 1.352E-6 3.183E-7 18.05 <.0001 0.0739 1.000
GiftAvg36 1 -0.0144 0.00506 8.14 0.0043 -0.0782 0.986
GiftAvgAll 1 0.00592 0.00543 1.19 0.2752 0.0326 1.006
GiftCnt36 1 0.0343 0.0305 1.27 0.2606 0.0397 1.035
GiftCntCard36 1 0.0737 0.0414 3.17 0.0751 0.0639 1.076
GiftTimeFirst 1 0.00440 0.00261 2.85 0.0914 0.0911 1.004
GiftTimeLast 1 -0.0410 0.00927 19.56 <.0001 -0.0925 0.960
IMP_DemAge 1 0.00452 0.00213 4.48 0.0344 0.0356 1.005
IMP_DemIncomeGroup 1 0.0784 0.0193 16.45 <.0001 0.0703 1.082
M_GiftAvgCard36 0 1 0.2776 0.0884 9.86 0.0017 1.320
PromCnt12 1 -0.0224 0.0132 2.90 0.0887 -0.0607 0.978
PromCnt36 1 0.0236 0.0116 4.13 0.0422 0.1005 1.024
PromCntCard36 1 -0.0362 0.0215 2.83 0.0925 -0.0909 0.964
PromCntCardAll 1 -0.0132 0.0140 0.88 0.3471 -0.0620 0.987
StatusCatStarAll 0 1 -0.0763 0.0392 3.79 0.0516 0.927
While not all the p-values are
less than 0.05, the model seems to have a better validation average square
error (and misclassification) than the model selected using the default
Significance Level settings.
In short, there is nothing sacred about 0.05. It is not unreasonable to
override the defaults of the Regression node to enable selection from a richer
collection of potential models. On the other hand, most of the reduction in the
fit statistics occurs during inclusion of the first 10 inputs. If you seek a
parsimonious model, it is reasonable to use a smaller value for the Stay Significance
parameter

Classical
regression analysis makes no assumptions about the distribution of inputs. The
only assumption is that the expected value of the target (or some function
thereof) is a linear combination of input measurements.
Why should you worry
about extreme input distributions?
There are at
least two compelling reasons.
First, in most real-world
applications, the relationship between expected target value and input value
does not increase without bound. Rather, it typically tapers off to some
horizontal asymptote. Standard regression models are unable to accommodate such
a relationship.
Second, as a point expands
from the overall mean of a distribution, the point has more influence, or leverage, on model fit. Models built on
inputs with extreme distributions attempt to optimize fit for the most extreme
points at the cost of fit for the bulk of the data, usually near the input
mean. This can result in an exaggeration or an understating of an input's
association with the target, or both.
The first
concern can be addressed by abandoning standard regression models for more
flexible modeling methods. Abandoning standard regression models is often done
at the cost of model interpretability and, more importantly, failure to address
the second concern: leverage.


A simpler and, arguably,
more effective approach is to transform offending inputs to less extreme forms
and build models on these transformed inputs, which not only reduces the
influence of extreme cases, but also creates an asymptotic association between
input and target on the original input scale.
 Transforming Inputs
Transforming Inputs
Regression models (such as clustering models) are sensitive to extreme or outlying values in the input space.
Inputs with highly skewed or highly kurtotic distributions can be selected over
inputs that yield better overall predictions. To avoid this problem, analysts
often regularize the input distributions using a simple transformation.
The benefit of this approach is improved model performance. The cost, of
course, is increased difficulty in model interpretation.
The Transform Variables tool enables you to easily apply standard
transformations (in addition to the specialized ones seen in Chapter 3) to a
set of inputs.
Remove the connection between the Data Partition node and the Impute node.

Select the Modify tab.
Drag a Transform Variables
tool into the diagram workspace.
Connect the Data Partition node to the Transform Variables node.
Connect the Transform Variables node to the Impute node.
Adjust the diagram icons for aesthetics.

The Transform Variables node is placed before the
Impute node to keep the imputed values at the average (or center of mass) of
the model inputs.
Select the Variables .
property of the Transform Variables node.
The Variables
- Trans window opens.

Select all inputs with Gift in the
name.

Select Explore . . The Explore
window opens.

The GiftAvg and GiftCnt inputs show some degree of skewness in their
distribution. The GiftTime inputs do not. To regularize the skewed distributions,
use the log transformation. For these inputs, the order of magnitude of the
underlying measure will predict the target rather than the measure itself.
Close the Explore window.
Deselect the two inputs with GiftTime in their names.

Select Method Log for one of the remaining
selected inputs. The selected method changes from Default to Log for
the GiftAvg and GiftCnt
inputs.

Select OK to close the Variables
- Trans window.
Run the Transform Variables node and view the results.
Maximize the Output window and examine lines 20-30.
Input Output
Input Name Role Level Output Name Level Formula
GiftAvg36 INPUT INTERVAL LOG_GiftAvg36 INTERVAL log(GiftAvg36 + 1)
GiftAvgAll INPUT INTERVAL LOG_GiftAvgAll INTERVAL log(GiftAvgAll + 1)
GiftAvgCard36 INPUT INTERVAL LOG_GiftAvgCard36 INTERVAL log(GiftAvgCard36 + 1)
GiftAvgLast INPUT INTERVAL LOG_GiftAvgLast INTERVAL log(GiftAvgLast + 1)
GiftCnt36 INPUT INTERVAL LOG_GiftCnt36 INTERVAL log(GiftCnt36 + 1)
GiftCntAll INPUT INTERVAL LOG_GiftCntAll INTERVAL log(GiftCntAll + 1)
GiftCntCard36 INPUT INTERVAL LOG_GiftCntCard36 INTERVAL log(GiftCntCard36 + 1)
GiftCntCardAll INPUT INTERVAL LOG_GiftCntCardAll INTERVAL log(GiftCntCardAll + 1)
Notice the Formula
column. While a log transformation was specified, the
actual transformation used was log(input
+ 1). This default action of the Transform Variables tool avoids problems with
0-values of the underlying inputs.
Close the Transform Variables - Results window.
Run the diagram from the Regression node and view the results.
Examine lines 1653 to 1680 the Output window.
Summary of Stepwise Selection
Effect Number Score Wald
Step Entered Removed DF In Chi-Square Chi-Square Pr > ChiSq
1 LOG_GiftCntCard36 1 1 107.6034 <.0001
2 GiftTimeLast 1 2 29.0312 <.0001
3 DemMedHomeValue 1 3 24.8434 <.0001
4 LOG_GiftAvgAll 1 4 28.9692 <.0001
5 IMP_DemIncomeGroup 1 5 13.8240 0.0002
6 GiftTimeFirst 1 6 7.1299 0.0076
7 IMP_DemAge 1 7 4.1407 0.0419
8 LOG_GiftAvgLast 1 8 2.6302 0.1048
9 PromCntCard12 1 9 1.8469 0.1741
10 StatusCatStarAll 1 10 1.8604 0.1726
11 IMP_LOG_GiftAvgCard36 1 11 1.4821 0.2234
LOG_GiftAvgAll 1 10 0.4217 0.5161
13 M_LOG_GiftAvgCard36 1 11 2.0584 0.1514
14 LOG_GiftCnt36 1 12 1.8949 0.1687
15 DemPctVeterans 1 13 0.3578 0.5498
16 DemPctVeterans 1 12 0.3577 0.5498
The selected model, based on the CHOOSE=VERROR criterion,
is the model trained in Step 15. It consists of the following effects:
Intercept DemMedHomeValue DemPctVeterans GiftTimeFirst GiftTimeLast IMP_DemAge IMP_DemIncomeGroup IMP_LOG_GiftAvgCard36 LOG_GiftAvgLast LOG_GiftCnt36 LOG_GiftCntCard36 M_LOG_GiftAvgCard36 PromCntCard12 StatusCatStarAll
The stepwise selection process took 16 steps, and
the selected model came from step 15. Notice that many of the inputs selected
are log transformations of the original.
Lines 1710 to 1750 show more statistics from the selected model.
Analysis of Maximum Likelihood
Estimates
Standard Wald Standardized
Parameter DF Estimate Error Chi-Square Pr > ChiSq Estimate Exp(Est)
Intercept 1 0.2908 0.3490 0.69 0.4047 1.338
DemMedHomeValue 1 1.381E-6 3.173E-7 18.94 <.0001 0.0754 1.000
DemPctVeterans 1 0.00155 0.00260 0.36 0.5498 0.00977 1.002
GiftTimeFirst 1 0.00210 0.000958 4.82 0.0281 0.0436 1.002
GiftTimeLast 1 -0.0369 0.00810 20.70 <.0001 -0.0831 0.964
IMP_DemAge 1 0.00419 0.00214 3.85 0.0498 0.0330 1.004
IMP_DemIncomeGroup 1 0.0821 0.0193 18.03 <.0001 0.0737 1.086
IMP_LOG_GiftAvgCard36 1 -0.1880 0.0985 3.65 0.0562 -0.0479 0.829
LOG_GiftAvgLast 1 -0.1101 0.0828 1.77 0.1837 -0.0334 0.896
LOG_GiftCnt36 1 0.1579 0.1165 1.84 0.1752 0.0417 1.171
LOG_GiftCntCard36 1 0.1983 0.1269 2.44 0.1183 0.0610 1.219
M_LOG_GiftAvgCard36 0 1 0.1111 0.0657 2.86 0.0910 1.117
PromCntCard12 1 -0.0418 0.0259 2.60 0.1069 -0.0305 0.959
StatusCatStarAll 0 1 -0.0529 0.0388 1.86 0.1729 0.948
Odds Ratio Estimates
Point
Effect Estimate
DemMedHomeValue 1.000
DemPctVeterans 1.002
GiftTimeFirst 1.002
GiftTimeLast 0.964
IMP_DemAge 1.004
IMP_DemIncomeGroup 1.086
IMP_LOG_GiftAvgCard36 0.829
LOG_GiftAvgLast 0.896
LOG_GiftCnt36 1.171
LOG_GiftCntCard36 1.219
M_LOG_GiftAvgCard36 0 vs 1 1.249
PromCntCard12 0.959
StatusCatStarAll 0 vs 1 0.900
Select View Model Iteration Plot.

Again, the selected model (based on minimum
average squared error) occurs in step 15. The actual value of average squared
error for this model is slightly lower than that for the model with the
untransformed inputs.
Select Select Chart Misclassification Rate.

The misclassification rate with the transformed
input is also lower than that for the untransformed inputs. However, the model
with the lowest misclassification rate comes from step 6. If you want to
optimize on misclassification rate, you must change this property in the
Regression node's property sheet.

Categorical inputs present
another problem for regressions. To represent these non-numeric inputs in a
model, you must convert them to some sort of numeric values. This conversion is
most commonly done by creating design variables (or dummy variables), with each design variable representing, roughly,
one level of the categorical input. (The total number of design variables
required is, in fact, one less than the number of inputs.) A single categorical
input can vastly increase a model's degrees of freedom, which, in turn,
increases the chances of a model overfitting.

There are many remedies to this problem. One of
the simplest remedies is to use domain knowledge to reduce the number of levels
of the categorical input.
 Recoding Categorical Inputs
Recoding Categorical Inputs
The demonstration shows how to use the Replacement tool to facilitate
combining input levels.
Remove the connection between the Transform Variables
node and the Impute node.

Select the Modify tab.
Drag a Replacement tool into the diagram workspace.
Connect the Transform Variables node to the Replacement node.
Connect the Replacement node to the Impute node.
Select Replacement Editor .
from the Replacement node Properties panel. A confirmation dialog box opens.

Select Yes. The Replacement
Editor opens.
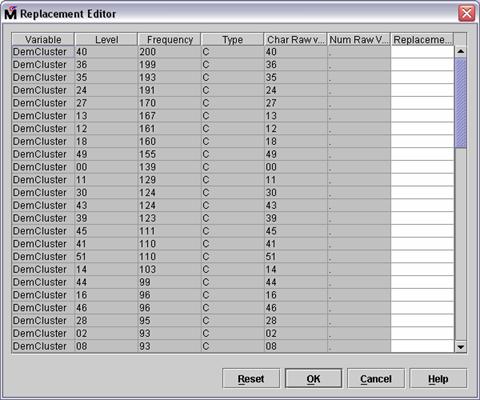
The Replacement Editor lists
all levels of all categorical inputs. You can use the Replacement column to
reassign values to any of the levels.
The input with the largest
number of levels is DemCluster, which has so many levels that consolidating the levels using the
Replacement Editor would be an arduous task. (Another, autonomous method for
consolidating the levels of DemCluster (or any categorical input) is presented as a special topic in Chapter
9.)
For this demonstration,
combine the levels of another input, StatusCat96NK
Scroll the Replacement Editor to view the levels of StatusCat96NK

The input has six levels,
plus a level to represent unknown values (which do not occur in the training
data). The levels of StatusCat96NK will be consolidated as follows:
Levels A and S (active and star donors) indicate consistent donors and are
grouped into a single level, A.
Levels F and N (first-time and new donors) indicate new donors and are
grouped into a single level, N.
Levels E and L (inactive and lapsing donors) indicate lapsing donors
and are grouped into a single level L.
Type A in the Replacement field for StatusCat96NK levels A and S.
Type N in the Replacement field for StatusCat96NK levels F and N.
Type L in the Replacement field for StatusCat96NK levels L and E.
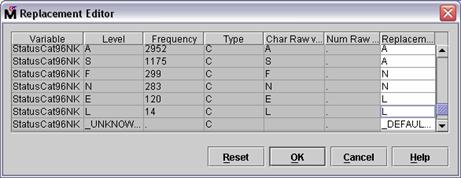
Select OK to close
the Replacement Editor.
Run the Replacement node and view the results.
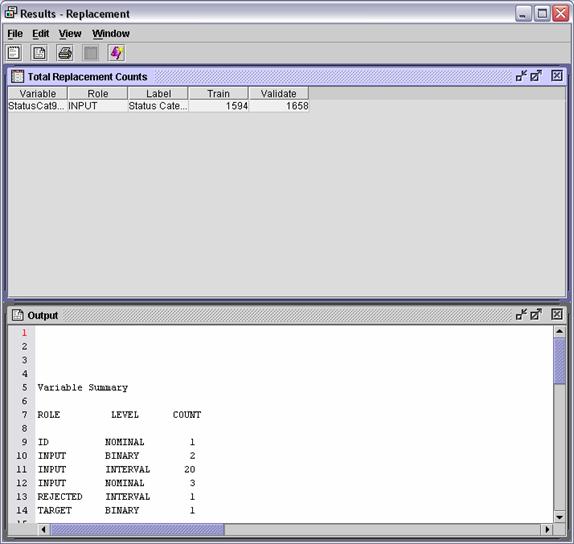
The Total Replacement Counts
window shows the number of replacements that occurr in the training and
validation data.
Select View Model Replaced Levels. The
Replaced Levels window opens.
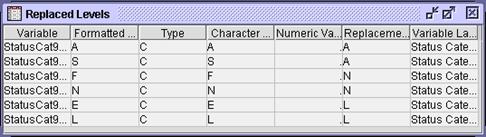
The replaced level values are
consistent with expectations.
Close the Results window.
Run the Regression node and view the results.
View lines 2310-2340 of the
Output window.
Summary
of Stepwise Selection
Effect Number Score Wald
Step Entered Removed DF In Chi-Square Chi-Square Pr > ChiSq
1 LOG_GiftCntCard36 1 1 107.6034 <.0001
2 GiftTimeLast 1 2 29.0312 <.0001
3 DemMedHomeValue 1 3 24.8434 <.0001
4 LOG_GiftAvgAll 1 4 28.9692 <.0001
5 IMP_DemIncomeGroup 1 5 13.8240 0.0002
6 GiftTimeFirst 1 6 7.1299 0.0076
7 IMP_DemAge 1 7 4.1407 0.0419
8 REPL_StatusCat96NK 2 8 5.2197 0.0735
9 IMP_LOG_GiftAvgCard36 1 9 2.4956 0.1142
10 M_LOG_GiftAvgCard36 1 10 1.6207 0.2030
11 StatusCatStarAll 1 11 1.9076 0.1672
12 LOG_GiftCnt36 1 12 1.5708 0.2101
13 LOG_GiftAvgLast 1 13 1.4316 0.2315
14 LOG_GiftAvgAll 1 12 0.2082 0.6482
15 PromCntCardAll 1 13 0.6704 0.4129
16 PromCnt36 1 14 1.0417 0.3074
17 PromCnt12 1 15 0.9800 0.3222
18 PromCntAll 1 16 1.0446 0.3068
19 M_DemAge 1 17 0.4815 0.4877
20 LOG_GiftCntAll 1 18 0.3887 0.5330
21 LOG_GiftCntAll 1 17 0.3886 0.5330
The REPL_StatusCat96NK input (created from the original StatusCat96NK input) is included in the stepwise selection process. The three-level
input is represented by two degrees of freedom.
View lines 2422-2423 of the Output window.
REPL_StatusCat96NK A vs N 0.822
REPL_StatusCat96NK L vs N 1.273
Based
on the odds ratios, active donors in the 96NK campaign are less likely than new
donors to contribute in the 97NK campaign. On the other hand, lapsing donors in
the 96NK campaign are more likely than new donors to contribute in the 97NK
campaign.
Select View
Model
Iteration
Plot.
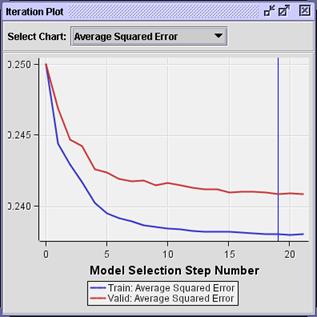
The
selected model from step 19 has, again, a slightly smaller average squared
error than previous models.
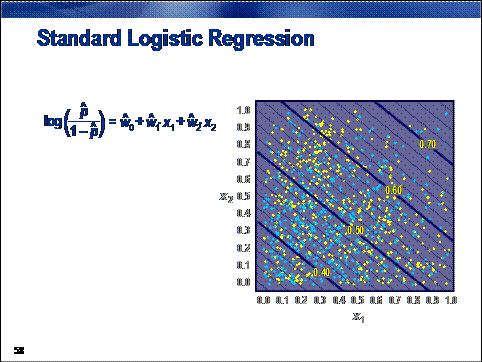
The Regression tool assumes (by
default) a linear and additive association between the inputs and the logit of
the target. If the true association is more complicated, such an assumption might
result in biased predictions. For decisions and rankings, this bias can (in
some cases) be unimportant. For estimates, this bias will appear as a higher
value for the validation average squared error fit statistic.
In the dot color problem, the (standard logistic regression) assumption
that the concentration of yellow dots increases toward the upper-right corner
of the unit square seems to be suspect.
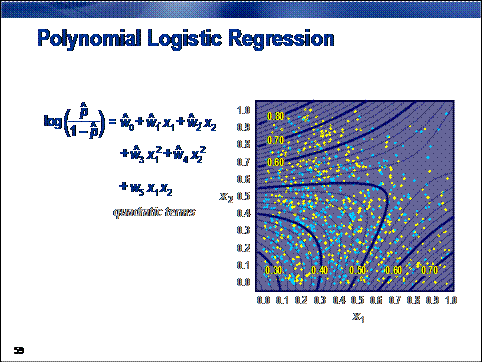
When minimizing prediction bias is important, you can increase the
flexibility of a regression model by adding polynomial combinations of the
model inputs. This enables predictions to better match the true input/target
association. It also increases the chances of overfitting while simultaneously
reducing the interpretability of the predictions. Therefore, polynomial
regression must be approached with some care.
In SAS Enterprise Miner, adding polynomial terms can be done selectively
or autonomously.
 Adding Polynomial Regression Terms Selectively
Adding Polynomial Regression Terms Selectively
This demonstration shows how to selectively add polynomial regression
terms.
You can modify the existing Regression node or add a new Regression node. If
you add a new node, you must configure the Polynomial Regression node to
perform the same tasks as the original. An alternative is to make a copy of the
existing node.
Right-click the Regression node
and select Copy from the
menu.
Right-click the diagram workspace and select Paste from the menu. A new Regression node is added with the
label Regression (2) to
distinguish it from the existing one.
Select the Regression (2)
node. The properties are identical to the existing node.
Rename the new regression node Polynomial Regression
Connect the Polynomial Regression node to the Impute node.
The Term Editor enables you to add specific polynomial
terms to the regression model.
Select Term Editor . from
the Polynomial Regression Properties panel. The Terms dialog box opens.

Suppose that you suspect an interaction between
home value and time since last gift. (Perhaps a recent change in property
values affected the donation patterns.)
Select DemMedHomeValue in the
Variables panel of the Terms dialog box.
Select the Add button,  . The DemMedHomeValue input
is added to the Term panel.
. The DemMedHomeValue input
is added to the Term panel.
Repeat for GiftTimeLast

Select Save. An
interaction between the selected inputs is now available for consideration by
the regression node.
Similarly, suppose that you suspect a parabola-shaped
relationship between donation and donor age. (Donation odds increase with age,
peak, and then decline with age.)
Select IMP_DemAge
Select the Add button,  . The IMP_DemAge input
is added to the Term panel.
. The IMP_DemAge input
is added to the Term panel.
Select the Add button,  again.
Another IMP_DemAge input
is added to the Term panel.
again.
Another IMP_DemAge input
is added to the Term panel.
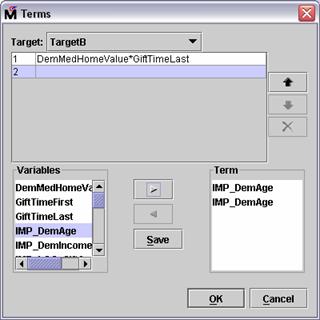
Select Save. A quadratic
age term is available for consideration by the model.

Select OK to close the Terms
dialog box.
To use the terms you defined in the Terms dialog
box, you must enable the User Terms option in the Regression node.
Select User Terms Yes in the Polynomial Regression
Properties panel.
Run the Polynomial Regression node and view the results.
Scroll the Output window to lines 2515-2540.
Summary of Stepwise Selection
Effect Number Score Wald
Step Entered Removed DF In Chi-Square Chi-Square Pr > ChiSq
1 LOG_GiftCntCard36 1 1 107.6034 <.0001
2 GiftTimeLast 1 2 29.0312 <.0001
3 DemMedHomeValue*GiftTimeLast 1 3 26.3762 <.0001
4 LOG_GiftAvgAll 1 4 29.2016 <.0001
5 IMP_DemIncomeGroup 1 5 13.8523 0.0002
6 GiftTimeFirst 1 6 7.1518 0.0075
7 IMP_DemAge 1 7 4.0914 0.0431
8 IMP_DemAge*IMP_DemAge 1 8 12.2214 0.0005
9 M_DemAge 1 9 4.1796 0.0409
10 REPL_StatusCat96NK 2 10 5.7905 0.0553
11 LOG_GiftAvgLast 1 11 2.3447 0.1257
12 StatusCatStarAll 1 12 1.8360 0.1754
13 LOG_GiftCnt36 1 13 1.3030 0.2537
14 M_LOG_GiftAvgCard36 1 14 1.6761 0.1954
15 IMP_LOG_GiftAvgCard36 1 15 1.7173 0.1900
16 LOG_GiftAvgAll 1 14 0.3704 0.5428
17 PromCntCardAll 1 15 1.0003 0.3172
18 PromCntAll 1 16 1.2101 0.2713
19 PromCnt12 1 17 0.6678 0.4138
20 PromCnt36 1 18 1.3816 0.2398
21 LOG_GiftCntAll 1 19 0.4570 0.4990
22 LOG_GiftAvgAll 1 20 0.3898 0.5324
23 LOG_GiftAvgAll 1 19 0.3897 0.5325
The stepwise selection summary shows the
polynomial terms added in steps 3 and 8.
View the Iteration Plot window.
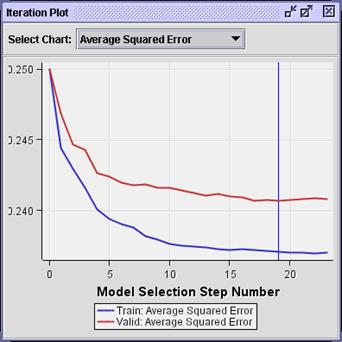
While present in the selected model, the
interaction terms appear to have negligible effect on the model performance (at
least for average squared error).
This begs the question: How do you know which
non-linear terms to include in a model?
Unfortunately, there is no simple solution to this
question in SAS Enterprise Miner, short of trying all of them
Adding Polynomial Regression Terms
Autonomously
(Self-Study)
SAS Enterprise Miner has the ability to add every polynomial combination of inputs to a regression model.
Obviously, this feature must be used with some care, because the number of
polynomial input combinations increases rapidly with input count.
For instance, the PVA97NK data
set has 20 interval inputs. If you want to consider every quadratic combination
of these 20 inputs, your selection procedure must sequentially slog through
more than 200 inputs. This is not an overwhelming task for today's fast
computers, but there is a shortcut that many analysts use to reduce this count.
The trick is to only consider polynomial expressions of those inputs found
to be linearly related to the logit of the target. That is, start with those
inputs selected by the original regression model. A simple modification to your
analysis diagram makes this possible.
Delete the connection between the Impute
node and the Polynomial Regression
node.
Connect the Regression node to the Polynomial Regression node.

Right-click the Polynomial Regression node
and select Update from the menu.
A Status dialog box informs you of the completion of the update process.
Select OK to close the Status
dialog box.
Select Variables . from
the Polynomial Regression Properties panel.
All inputs not selected in the original regression's
stepwise procedure are rejected.
Select OK to close the Variables
dialog box.
Select Polynomial Terms Yes in the Polynomial Regression
Properties panel. This adds all quadratic combinations of the interval inputs.
You can increase this to a higher order polynomial by
changing the Polynomial Degree field.
Select User Terms No. The terms added in the last
demonstration will be included by specifying the Polynomial Terms option.
Run the Polynomial Regression node and view the results. (This might take
a few minutes to complete on slower computers.)
Scroll to the bottom of the Output window.
NOTE: File view has been
truncated.
Refer to C:Documents and
SettingsusernameMy DocumentsMy SAS Files9.1EM_ProjectsMy
ProjectWorkspacesEMWS2Reg2EMOUTPUT.out
on this server for entire
file contents.
The amount of output generated by the selection history exceeds the 10,000-line,
client-transfer limit of SAS Enterprise Miner. To view the complete output
listing, you must open the referenced file.
Doing so reveals a 121-step and 18,000-line input
selection free-for-all. The selection summary is shown below.
Summary of Stepwise Selection
Effect Number Score Wald
Step Entered Removed DF In Chi-Square Chi-Square Pr > ChiSq
1 IMP_DemAge*LOG_GiftCntCard36 1 1 112.3900 <.0001
2 GiftTimeLast*LOG_GiftAvgLast 1 2 50.4645 <.0001
3 DemMedHomeValue*IMP_DemIncomeGroup 1 3 35.6614 <.0001
4 GiftTimeFirst*IMP_DemIncomeGroup 1 4 15.9535 <.0001
5 DemMedHomeValue*GiftTimeLast 1 5 5.1609 0.0231
6 DemMedHomeValue*IMP_DemIncomeGroup 1 4 0.0257 0.8726
7 IMP_DemAge*PromCntCardAll 1 5 4.5051 0.0338
8 GiftTimeFirst*LOG_GiftCnt36 1 6 4.6421 0.0312
9 GiftTimeLast*LOG_GiftCntCard36 1 7 8.0742 0.0045
10 GiftTimeLast*IMP_DemIncomeGroup 1 8 3.7680 0.0522
11 StatusCatStarAll 1 9 4.0508 0.0442
12 M_LOG_GiftAvgCard36 1 10 4.9476 0.0261
13 IMP_DemIncomeGroup*IMP_DemIncomeGroup 1 11 3.3268 0.0682
14 IMP_DemIncomeGroup*LOG_GiftAvgLast 1 12 5.6563 0.0174
15 GiftTimeLast 1 13 6.6747 0.0098
16 GiftTimeLast*IMP_DemIncomeGroup 1 12 0.0375 0.8465
17 LOG_GiftCntCard36 1 13 5.4244 0.0199
18 IMP_DemAge*LOG_GiftAvgLast 1 14 5.0260 0.0250
19 IMP_DemAge*IMP_DemAge 1 15 5.7455 0.0165
20 IMP_DemAge 1 16 5.2865 0.0215
21 M_DemAge 1 17 8.9336 0.0028
22 LOG_GiftAvgLast*PromCntAll 1 18 2.6281 0.1050
23 LOG_GiftCnt36*LOG_GiftCnt36 1 19 2.5730 0.1087
24 GiftTimeFirst*IMP_DemIncomeGroup 1 18 0.0289 0.8651
25 GiftTimeFirst*PromCntAll 1 19 3.6941 0.0546
26 IMP_DemAge*LOG_GiftAvgLast 1 18 0.3456 0.5566
27 IMP_DemAge*LOG_GiftCntCard36 1 17 0.2592 0.6107
28 GiftTimeLast*PromCntAll 1 18 2.3912 0.1220
29 GiftTimeFirst*IMP_DemAge 1 19 1.9879 0.1586
30 LOG_GiftCnt36*PromCntCardAll 1 20 4.8338 0.0279
31 REPL_StatusCat96NK 2 21 3.4798 0.1755
32 IMP_DemAge*IMP_DemIncomeGroup 1 22 1.1337 0.2870
33 IMP_DemAge*IMP_LOG_GiftAvgCard36 1 23 1.0241 0.3116
34 GiftTimeLast*IMP_LOG_GiftAvgCard36 1 24 3.8889 0.0486
35 IMP_LOG_GiftAvgCard36 1 25 3.6415 0.0564
36 IMP_DemAge*IMP_LOG_GiftAvgCard36 1 24 0.2008 0.6541
37 IMP_LOG_GiftAvgCard36*LOG_GiftAvgLast 1 25 5.6166 0.0178
38 IMP_LOG_GiftAvgCard36*LOG_GiftCntCard36 1 26 2.8395 0.0920
39 LOG_GiftAvgLast 1 27 1.4026 0.2363
40 LOG_GiftAvgLast*LOG_GiftCntCard36 1 28 1.0598 0.3033
41 M_LOG_GiftAvgCard36 1 27 0.2257 0.6348
42 GiftTimeLast*PromCnt12 1 28 0.9554 0.3284
43 IMP_LOG_GiftAvgCard36*PromCnt36 1 29 1.1580 0.2819
44 GiftTimeFirst*PromCnt36 1 30 1.2396 0.2655
45 GiftTimeFirst*PromCntAll 1 29 0.0060 0.9380
(Continued on the next page.)
46 IMP_LOG_GiftAvgCard36*LOG_GiftCntCard36 1 28 0.4424 0.5060
47 IMP_LOG_GiftAvgCard36*IMP_LOG_GiftAvgCard36 1 29 1.0828 0.2981
48 LOG_GiftCnt36*PromCntAll 1 30 1.0412 0.3075
49 IMP_DemAge*PromCntCardAll 1 29 0.3676 0.5443
50 LOG_GiftAvgLast*PromCntCardAll 1 30 2.0774 0.1495
51 LOG_GiftCnt36*PromCntCardAll 1 29 0.3967 0.5288
52 PromCnt36*PromCntCardAll 1 30 1.2143 0.2705
53 GiftTimeLast*PromCntAll 1 29 0.4198 0.5170
54 LOG_GiftAvgLast*PromCnt36 1 30 0.9148 0.3388
55 PromCntAll 1 31 1.0177 0.3131
56 IMP_DemIncomeGroup*LOG_GiftCntCard36 1 32 0.8736 0.3500
57 IMP_DemIncomeGroup*LOG_GiftCnt36 1 33 1.3926 0.2380
58 GiftTimeLast*LOG_GiftCnt36 1 34 1.9062 0.1674
59 DemMedHomeValue*GiftTimeFirst 1 35 0.8606 0.3536
60 DemMedHomeValue*PromCnt12 1 36 1.7609 0.1845
61 DemMedHomeValue*DemMedHomeValue 1 37 1.6746 0.1956
62 IMP_LOG_GiftAvgCard36*PromCnt12 1 38 1.0289 0.3104
63 LOG_GiftAvgLast*PromCnt12 1 39 1.1348 0.2867
64 LOG_GiftCnt36*PromCnt12 1 40 0.8804 0.3481
65 PromCntAll 1 39 0.1284 0.7201
66 IMP_DemAge*PromCntAll 1 40 0.9530 0.3290
67 IMP_DemAge*PromCnt36 1 41 0.7239 0.3949
68 IMP_LOG_GiftAvgCard36*PromCntAll 1 42 0.7922 0.3734
69 GiftTimeFirst*IMP_LOG_GiftAvgCard36 1 43 1.1685 0.2797
70 IMP_DemIncomeGroup*PromCnt36 1 44 0.8058 0.3694
71 IMP_DemIncomeGroup*PromCntCardAll 1 45 1.7767 0.1826
72 IMP_DemIncomeGroup*PromCnt12 1 46 3.3905 0.0656
73 LOG_GiftAvgLast*PromCnt12 1 45 0.1157 0.7337
74 IMP_DemAge*IMP_DemIncomeGroup 1 44 0.3121 0.5764
75 IMP_DemIncomeGroup*PromCntAll 1 45 1.5760 0.2093
76 DemMedHomeValue*IMP_DemAge 1 46 0.7067 0.4005
77 DemMedHomeValue 1 47 0.8369 0.3603
78 GiftTimeLast*PromCntCardAll 1 48 0.6305 0.4272
79 GiftTimeLast*PromCnt36 1 49 1.3586 0.2438
80 IMP_DemAge*IMP_LOG_GiftAvgCard36 1 50 0.5447 0.4605
81 IMP_DemAge*LOG_GiftAvgLast 1 51 1.8152 0.1779
82 IMP_LOG_GiftAvgCard36*PromCntCardAll 1 52 0.5547 0.4564
83 PromCnt12*PromCnt12 1 53 0.4997 0.4796
84 PromCnt36*PromCntCardAll 1 52 0.2620 0.6088
85 GiftTimeFirst*IMP_LOG_GiftAvgCard36 1 51 0.3309 0.5651
86 GiftTimeFirst*GiftTimeLast 1 52 0.9405 0.3322
87 PromCnt12 1 53 0.6663 0.4143
88 PromCnt36 1 54 1.1938 0.2746
89 IMP_LOG_GiftAvgCard36*PromCnt12 1 53 0.1271 0.7215
90 LOG_GiftCnt36*LOG_GiftCntCard36 1 54 0.9120 0.3396
91 LOG_GiftCntCard36 1 53 0.1168 0.7326
92 LOG_GiftCntCard36*LOG_GiftCntCard36 1 54 1.2887 0.2563
93 LOG_GiftCntCard36*PromCnt36 1 55 0.8773 0.3489
94 PromCntCardAll 1 56 0.9834 0.3214
95 GiftTimeLast*PromCnt36 1 55 0.3743 0.5407
96 GiftTimeLast*PromCnt12 1 54 0.0612 0.8046
97 PromCnt36*PromCnt36 1 55 1.0367 0.3086
98 LOG_GiftAvgLast*LOG_GiftCnt36 1 56 0.7673 0.3811
99 GiftTimeLast*LOG_GiftCnt36 1 55 0.3944 0.5300
100 LOG_GiftCntCard36*PromCntCardAll 1 56 0.8257 0.3635
(Continued on the next page.)
101 LOG_GiftCntCard36*PromCntAll 1 57 2.3132 0.1283
102 GiftTimeFirst*PromCnt36 1 56 0.3471 0.5558
103 GiftTimeFirst*LOG_GiftCntCard36 1 57 1.6283 0.2019
104 LOG_GiftCntCard36*PromCnt36 1 56 0.0007 0.9792
105 LOG_GiftCnt36*PromCntAll 1 55 0.2986 0.5848
106 LOG_GiftCntCard36*PromCnt12 1 56 2.1837 0.1395
107 LOG_GiftCnt36*PromCnt12 1 55 0.1815 0.6701
108 GiftTimeLast 1 54 0.4189 0.5175
109 LOG_GiftCntCard36*PromCnt36 1 55 0.9461 0.3307
110 DemMedHomeValue*PromCnt36 1 56 0.5590 0.4547
111 DemMedHomeValue*PromCnt12 1 55 0.4496 0.5025
112 DemMedHomeValue*PromCntCardAll 1 56 0.8854 0.3467
DemMedHomeValue*GiftTimeFirst 1 55 0.0000 0.9972
114 GiftTimeLast*IMP_DemIncomeGroup 1 56 0.6227 0.4300
115 PromCnt12*PromCntAll 1 57 0.5536 0.4568
116 PromCnt12*PromCntCardAll 1 58 0.5737 0.4488
117 GiftTimeFirst 1 59 0.4895 0.4842
118 GiftTimeFirst*GiftTimeLast 1 58 0.1034 0.7478
119 GiftTimeFirst*LOG_GiftAvgLast 1 59 1.4562 0.2275
120 GiftTimeLast 1 60 0.3704 0.5428
121 GiftTimeLast 1 59 0.3701 0.5430
Examine the iteration plot.

Surprisingly, the selected model comes from step 12 and involves only a
few regression terms.
Analysis of Maximum Likelihood Estimates
Standard Wald Standardized
Parameter DF Estimate Error Chi-Square Pr > ChiSq Estimate Exp(Est)
Intercept 1 0.0164 0.1395 0.01 0.9063 1.017
StatusCatStarAll 0 1 -0.0761 0.0378 4.05 0.0442 0.927
DemMedHomeValue*GiftTimeLast 1 7.885E-8 1.694E-8 21.67 <.0001 1.000
GiftTimeFirst*IMP_DemIncomeGroup 1 0.000345 0.000324 1.13 0.2872 1.000
GiftTimeFirst*LOG_GiftCnt36 1 0.00309 0.000920 11.26 0.0008 1.003
GiftTimeLast*IMP_DemIncomeGroup 1 0.00327 0.00157 4.34 0.0371 1.003
GiftTimeLast*LOG_GiftAvgLast 1 -0.0136 0.00265 26.42 <.0001 0.986
GiftTimeLast*LOG_GiftCntCard36 1 -0.0239 0.00695 11.86 0.0006 0.976
IMP_DemAge*LOG_GiftCntCard36 1 0.0114 0.00202 32.02 <.0001 1.012
IMP_DemAge*PromCntCardAll 1 -0.00032 0.000092 12.23 0.0005 1.000
Unfortunately, all but one of the selected terms is an
interaction.
While this model is the best predictor of PVA97NK response
found up to this time, it is nearly impossible to interpret. This is an
important factor to remember when considering polynomial regression models.
Exercises
Predictive Modeling Using
Regression
Return to the Chapter 4 Organics diagram in the Exercises project.
Explore the ORGANICS data source.
In preparation for regression, is any missing values imputation needed?
If yes, should you do this imputation before generating the decision tree
models? Why or why not?
Add an Impute node to the diagram and connect it to the Data Partition
node.
Change Default Input Method to Tree for both class and interval
variables. Create missing value indicator variables. Replace missing values for
GENDER with U for unknown.
Add a Regression node to the diagram and connect it to the Impute node.
Choose the stepwise selection and average squared error as the
selection criterion.
Run the Regression node and view the results. Which variables are
included in the final model? Which variables are important in this model?
In preparation for regression, are any transformations of the data
warranted? Why or why not?
Add a Transform Variables node to the diagram and connect it to the
Impute node.
The variable AFFL appears to be skewed to the
right. Use a square root transformation for AFFL. The variables BILL and LTIME also appear to be skewed to
the right. Use SAS Enterprise Miner to transform these variables to maximize
normality.
Run the Transform Variables node. Explore the exported training data.
Did the transformation of AFFL appear to result in a less
skewed distribution? What transformation was chosen for the variables BILL and LTIME
Add another Regression node to the diagram and connect it to the Transform
Variables node.
Choose the stepwise selection method and average squared error
selection criterion.
Run this new Regression node and view the results. Which variables are
included in the final model? Which variables are important in the model?
How do the validation average squared errors of the two regression
models compare? How do the regression models compare to the tree models?
Regression
models are a prolific and useful way to create predictions. New cases are
scored using a prediction formula. Inputs are selected via a sequential selection
process. Model complexity is controlled by fit statistics calculated on
validation data.
To
use regression models, there are several issues with which to contend that go
beyond the predictive modeling essentials. First, a mechanism for handling missing
input values must be included in the model development process. Second, methods
for handling extreme or outlying predictions should be included. Third, the
level-count of a categorical should be reduced to avoid overfitting. Finally,
the model complexity might need to be increased beyond what is provided by
standard regression methods. One approach to this is polynomial regression.
Polynomial regression models can be fit by hand with specific
interactions in mind. They also can be fit autonomously by selecting polynomial
terms from a list of all polynomial candidates.


Predictive
Modeling Using Regression
Right-click
the ORGANICS data source in
the Project Panel and select Explore.

Examine
the ORGANICS data table to reveal several
inputs with missing values. A more precise way to determine the extent of
missing values in this data set is to use the StatExplore node.
Connect
a StatExplore node to the ORGANICS data source in the diagram workspace.
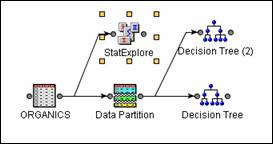
Select
the StatExplore node in the
diagram and examine the Properties panel.
Change
the option to Hide Rejected Variables to No
and change the option for Interval Variables to Yes using the menus.

Run
the StatExplore node and examine the Output window in the Results.
Class
Variable Summary Statistics
(maximum
500 observations printed)
Variable Role Numcat NMiss Mode
CLASS INPUT 4 0 Silver
GENDER INPUT 4 2512 F
NGROUP INPUT 8 674 C
REGION INPUT 6 465 South East
TV_REG INPUT 14 465 London
ORGYN TARGET 2 0 0
The variable GENDER has a
relatively large number of missing values.
Interval Variable Summary
Statistics
(maximum 500 variables
printed)
Variable ROLE Mean StdDev Non Missing Missing
AFFL INPUT 9 3 21138 1085
AGE INPUT 54 13 20715 1508
BILL INPUT 4421 7559 22223 0
LTIME INPUT 7 5 21942 281
The variables AFFL and AGE have
over 1000 missing values each.
Imputation
of missing values should be done prior to generating a regression model.
However, imputation is not necessary before generating a decision tree
model because a decision tree can use missing values in the same way as any other
data value in the data set.
Close the
StatExplore node results and return to the diagram workspace.
After you
add an Impute node, the diagram should appear as shown below.

Choose
the imputation methods.
Select
the Impute node in the
diagram.
To
use tree imputation as the default method of imputation, change the Default
Input Method for both class and interval variables to Tree using the menus.
To create
missing value indicator variables, change the Indicator Variable property to Unique
and the Indicator Variable Role to Input using the menus in the Properties panel.
To replace
missing values for the variable GENDER with U, first change Default Character Value to U. The Properties panel
should appear as shown.

Select Variables . . Change the value in
the Method column for the variable GENDER to Constant as shown below.

Select OK to confirm the change.
Add a Regression node to the
diagram as shown below.
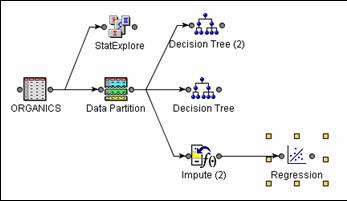
Choose
the stepwise selection and average squared error as the selection criterion.
Select
the Regression node in the
diagram.
Select
Selection Model Stepwise.
Select
Selection Criterion Validation
Error.
Run the
Regression node and view the results. The Output window shows which variables
are in the final model and which variables are important.
Line
658 lists the inputs included in the final model:
Intercept IMP_AFFL IMP_AGE IMP_GENDER M_AFFL M_AGE M_GENDER
Important
inputs can be ascertained by Wald Chi-Square, standardized estimates, and odds
ratio estimates.
Analysis of Maximum Likelihood
Estimates
Standard Wald Standardized
Parameter DF Estimate Error Chi-Square Pr > ChiSq Estimate Exp(Est)
Intercept 1 -0.7674 0.1336 33.01 <.0001 0.464
IMP_AFFL 1 0.2513 0.00721 1215.16 <.0001 0.4637 1.286
IMP_AGE 1 -0.0534 0.00179 895.19 <.0001 -0.3786 0.948
IMP_GENDER
F 1 0.9688 0.0480 407.57 <.0001 2.635
IMP_GENDER
M 1 0.0485 0.0528 0.84 0.3584 1.050
M_AFFL 0 1 -0.1276 0.0464 7.56 0.0060 0.880
M_AGE 0 1 -0.1051 0.0408 6.63 0.0100 0.900
M_GENDER 0 1 -0.2324 0.0767 9.18 0.0024 0.793
Odds Ratio Estimates
Point
Effect Estimate
IMP_AFFL 1.286
IMP_AGE 0.948
IMP_GENDER
F vs U 7.287
IMP_GENDER
M vs U 2.903
M_AFFL 0 vs 1 0.775
M_AGE 0 vs
1 0.810
M_GENDER 0 vs 1 0.628
Important inputs include IMP_AFFL IMP_AGE, and IMP_GENDER
Close the
regression results and return to the diagram workspace.
Explore
the input distributions.
Select the ORGANICS node and select Variables . in the Properties
panel.
Select all interval input
variables.
Select Explore . .
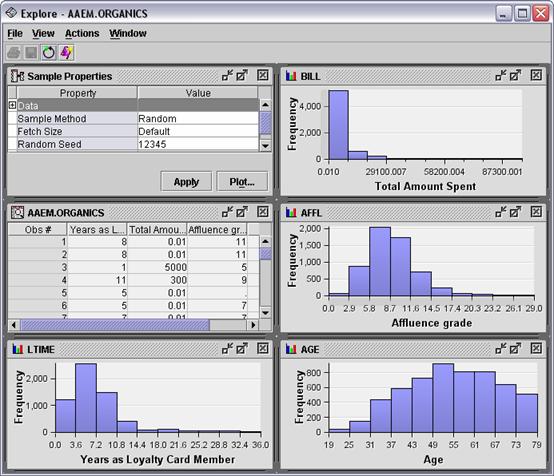
The variables AFFL BILL, and LTIME are skewed to the right and
might need to be transformed for a regression. This is evident in the
histograms that can be viewed in the exploration tool available in the Input
Data node and other nodes.
Connect a Transform Variables node as shown below.

Transform inputs.
Select Variables . in the Transform Variables node's Properties panel.
In the Method column for the
variable IMP_AFFL, select Square
Root from the menu. In the Method column for the variables BILL and IMP_LTIME, select Max. Normal from the menu. The
Variables window should appear as shown below.
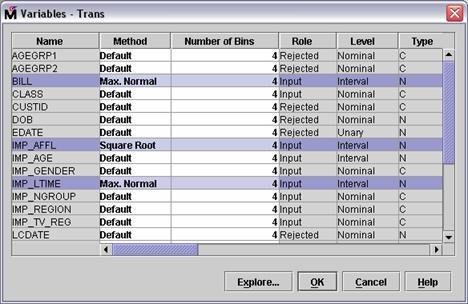
Select OK
to confirm the changes.
Run the Transform Variables node. Do not view the results. Instead,
select Exported Data . from
the Transform Variables node's Properties panel. The Exported Data - Transform
Variables window opens.
Select the Train data set and select Explore . .
In the
Explore window, select Actions
Plot . .
Select Histogram as the
type of chart and then select Next >.
Change the role of SQRT_IMP_AFFL to X.
Select Finish.

The
transformed variable appears to be less skewed than the original variable.
To view the transformations for the other variables,
close the graph and examine the Transformations window in the results. The
transformation chosen for the variable BILL was a square root transformation, and the
transformation for IMP_LTIME was the fourth root. You can confirm this by
opening the Results window and viewing lines 28-25 of the output.
Transformations
(Maximum 500 observations printed)
Input Input Output
Name Role Level Output Name Level Formula
BILL INPUT INTERVAL SQRT_BILL INTERVAL Sqrt(_SCALEVAR_)
IMP_AFFL INPUT INTERVAL SQRT_IMP_AFFL INTERVAL Sqrt(IMP_AFFL + 1)
IMP_LTIME INPUT INTERVAL PWR_IMP_LTIME INTERVAL (_SCALEVAR_)**0.25
Close the
results and return to the diagram workspace.
Add a second Regression node to the diagram as shown below.
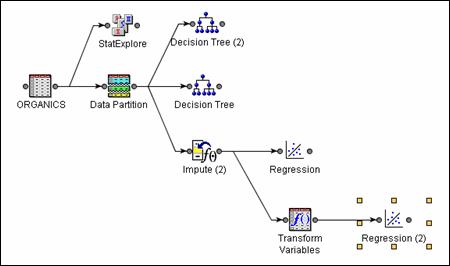
Choose
the stepwise selection and average squared error as the selection criterion.
Select
the Regression node in the
diagram.
Select
Selection Model Stepwise.
Select
Selection Criterion Validation
Error.
Run the
Regression node and view the results. The Output window shows which variables
are in the final model and which variables are important.
Line
563 lists the inputs included in the final model:
Intercept IMP_AGE IMP_GENDER SQRT_IMP_AFFL
Important
inputs can be ascertained by Wald Chi-Square, standardized estimates, and odds
ratio estimates.
Analysis of Maximum Likelihood
Estimates
Standard Wald Standardized
Parameter DF Estimate Error Chi-Square Pr > ChiSq Estimate Exp(Est)
Intercept 1 -4.1258 0.2170 361.43 <.0001 0.016
IMP_AGE 1 -0.0469 0.00209 503.99 <.0001 -0.3287 0.954
IMP_GENDER F 1 0.8995 0.0416 468.16 <.0001 2.458
IMP_GENDER M 1 -0.00905 0.0496 0.03 0.8551 0.991
SQRT_IMP_AFFL 1 1.5685 0.0571 755.15 <.0001 0.4545 4.799
Odds Ratio Estimates
Point
Effect
Estimate
IMP_AGE 0.954
IMP_GENDER F vs
U 5.990
IMP_GENDER M vs
U 2.414
SQRT_IMP_AFFL 4.799
Important inputs include SQRT_IMP_AFFL IMP_AGE, and IMP_GENDER
Model fit comparisons.
Examine the Fit
Statistics window.
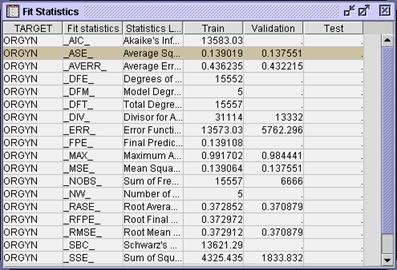
The
validation average squared error for this model equals 0.1376.
Open the Results
window for the original regression and examine the Fit Statistics window.

The
validation average squared error for the original regression model equals
0.1365, or slightly lower. In this case, transforming the inputs does not
improve model fit.
Open the Results window for
the original tree model and examine the Fit Statistics window.
The average squared error of the tree model is
smaller. It appears that the regression models are less adept at modeling the
association between inputs and target.



























































































