Paralelismul si calculul vectorial
In multe stiinte matematica fizica chimia ,
informatica si in practica se intalnesc
diverse feluri de marimi .Exista marimi complet caracterizate de un singur
numar numite marimi scalare .Alte marimi
sunt caracterizate de mai multe numere .Ele se numesc marimi vectoriale .
Exemplu
Marimi scalare : lungimea uni fir prelungit (electric este de 15 m
:capacitatea unei sticle este de 2.5
l ; temperatura la care ingheata apa
este de 0C ; solutia ecuatiei este
3x+1=0 este x=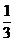
marimile vectoriale
pozitia uni avion in zbor la un moment dat se determina cu ajutorul a
trei numere care exprima cu ajutorul a
trei numere care exprima latitudinea ,
longitudinea si altitudinea aparatului
.Putem sa mai adaugam ca o a patra coordonare ,timplul ora minutul secunda la care avionul avea pozitia data ).
Exista programe de calculator ( un
fel de ghicitoare moderne ) care prezic care prezinta viitorul clientilor cu
ajutorul a 4 numere care prerezinta luna ziua anul nasteri .Ele presupun ca viitorul persoanei este
caracterizat de o marime vectoriala determainata de acese 4 numere .
O forta (in fizica )este caracterizata intr-un reper cartezian de doua numere (in plan ) sau de 3 numere ( in spatiu )
Exerciti : precizati care din urmatoarele marimi sunt marimi vectoriale .
Care
dintre urmatoarele marimi sunt saclare sau vectoriale :
Temperatura , masa pozitia unei locati pe o harta , lungimea pozitia unui submarin in ocean , viteza acceleratia , volumul ,
Rezolvare
Marimile vectoriale sunt : pozitia une locati pe o harta , pozitia unu
sub marin in ocean
Cuvantul vector are mai multe sensuri. In functie de domeniul in care este
folosit vom preciza vom preciza notiunea
de vector asa cum este ea cunoscuta in
algebra , geometrie si in fizica .
In algebra
Definite x-> =(x1
x2 x3 . .. . xn ) 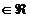 n n mai
mic sau egal cu 2 se numeste vector cu n componente , sau .vector n-dimensional .numarul natural n se numeste dimensiunea
vectorului
n n mai
mic sau egal cu 2 se numeste vector cu n componente , sau .vector n-dimensional .numarul natural n se numeste dimensiunea
vectorului 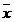 Rx se numeste spatiu real n - dimensional .
Rx se numeste spatiu real n - dimensional .
Exemple Vectori cu doua componente : (2,3) :(-1 a) a 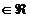
Vectori cu 3 componente :
(-1,-2,4);(x,y,-1), x, y 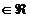
Egalitatea vectorilor ca si operatiile cu vectori , se defineste pentru vectori de aceleasi tip ( avabd
acelasi numar de componente )
Definitie
Fie n 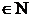 n
n 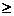 2 si x1 x2 x3 . .. . xn ,y1,
y2, . . yn numere
reale
2 si x1 x2 x3 . .. . xn ,y1,
y2, . . yn numere
reale
vectori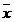 =(x1 x2 x3 . .. . xn ) si
=(x1 x2 x3 . .. . xn ) si 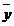 =( y1, y2, . . yn ) sunt egali daca x1 =y1 ,
x2 = y2, . ..x2 =yn*
=( y1, y2, . . yn ) sunt egali daca x1 =y1 ,
x2 = y2, . ..x2 =yn*
Exemplu (2,3) =(a ,3 )daca a = 2 ; (1,2,3,2) 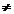 (2,a,b), a ,b
(2,a,b), a ,b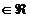
(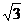 ,x,a,r,5)= (b,3-1,u,5 daca b=
,x,a,r,5)= (b,3-1,u,5 daca b=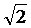 , x=3,a=1 si u =r
, x=3,a=1 si u =r
Definitie suma vectotilor 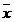 =( x1 x2 x3 . .. . xn ) si (y1, y2, . . yn )
este vectorul
=( x1 x2 x3 . .. . xn ) si (y1, y2, . . yn )
este vectorul 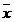 ,
, 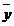 =( x1+ y1, x2+ y2* x n +yn )
=( x1+ y1, x2+ y2* x n +yn )
Produsul dintre vectorul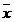 ( x1 x2 x3 . .. . xn ) si si scalarul
( x1 x2 x3 . .. . xn ) si si scalarul 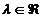 este vectorul
este vectorul 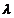
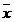 =
=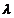 1 ,
1 ,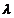 2 , . . ..
2 , . . ..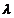 n
n
Observatie definitia vectorului
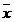 =( x1 x2
x3 . .. . xn ) si
=( x1 x2
x3 . .. . xn ) si 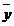 =( y1, y2, . . yn )
=( y1, y2, . . yn )
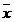 -
-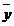 =( x1 - y1, x2 -y 2 , . . xn + yn )
=( x1 - y1, x2 -y 2 , . . xn + yn )
Exemplu (a,b)+(2,7)=(a+2,b+70 ,a, b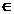 R ; 2(x,y)=(2x,2y), x,y
R ; 2(x,y)=(2x,2y), x,y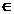 R;(2,3)-(1,2)=(1,1);(x,7,2)+(3,5;a)=(x+3,12,2+a),a,x
R;(2,3)-(1,2)=(1,1);(x,7,2)+(3,5;a)=(x+3,12,2+a),a,x 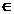 R;3(1,a,
R;3(1,a,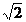 )= (3,3a,3
)= (3,3a,3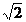 ), a
), a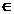 R
R
Definitie , o multime ordonata 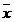 =( x1, x2, x3, . .. . , xn )
=( x1, x2, x3, . .. . , xn ) 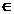 R3 se numeste vector cu 3 componente sau vector tridimensional sau vector in
spatiu (prin spatiu , de obicei intelegem spatiu cu trei dimensiuni )
R3 se numeste vector cu 3 componente sau vector tridimensional sau vector in
spatiu (prin spatiu , de obicei intelegem spatiu cu trei dimensiuni )
Exemplu
Vectori (x,y,z,)si(2,-1,4) sunt
egali daca x= 2,y=-1,z=4
Vectori(a,2,b)si (2,a,3)sunt egali
daca a =2 si b=3
Definitie suma vectorilor 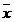 =( x1, x2, x3) si
=( x1, x2, x3) si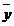 =( y1, y2, y3 )este vectorul
=( y1, y2, y3 )este vectorul 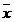 +
+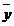 ( x1+ y1, x2 +y2 x 3 +y3 )
( x1+ y1, x2 +y2 x 3 +y3 )
Produsul dintre vectorul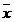 = ( x1, x2, x3) si scalarul
= ( x1, x2, x3) si scalarul 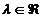 este vectorul
este vectorul 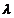
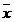 =(
=(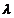 1 ,
1 ,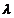 2 , . . ..
2 , . . ..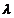 n)
n)
Exemple :
1)(2,a,b)+(a,1,1)=(a+2,a+1,b+!)
a,b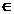 R
R
Pe un raft al
unui magazin se afla 30 de sticle de 2 l
si 15 sticle de 0,5 l de apa minerala pe
alt raft se afla 10 sticle de 2 l,5 sticle de 1l si 20 sticle de 0,5 de apa minerala (10,5,20).Vectorul
suma este (40,20,23)=(30,15,3)+(10,5,20)
si indica faptul ca pe ambele rafturi se afla 40 de sticle de 2l,20 de sticle de 1 l si 23 de sticle de 0,5l
Intr-o
urna sunt 7 bile rosi ,10 bile albe si 5
bile albastre .Matei extrage 2 bile rosi, 5 bile albe si 2 bile albastre .cate
bile rosi , albe si albastre se au ramas
in urna ?
Vectorul (7,10,5)
reprezinta repartizarea bilelor din urna si vectorul (2,5,2) reprezinta bilele extrase
.Atunci(7,10,5)-(2,5,2)=(5,5,3) reprezinta repartizarea bilelor ramase in
urna
5)Sa se calculeze vectorul
3.(2,a,3)=(6,3a,9) a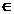 R
R

