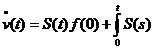Problema
Cauchy abstracta
1 Solutii clasice si moderate.
Proprietati.
Fie X un spatiu Banach real sau complex ,
S =  un C
un C - semigrup si
- semigrup si
A : D(A) 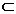 X
X 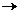 X generatorul sau infinitezimal.
X generatorul sau infinitezimal.
Pentru fiecare 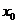

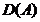 problema Cauchy
omogena
problema Cauchy
omogena

are o unica solutie
x(t) = S(t)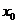
 .
.
In
continuare studiem problema Cauchy neomogena descrisa de sistemul
(S)
unde T  ( 0,
( 0, ], f : [ 0,T )
], f : [ 0,T ) 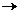 X ,
X ,  .
.
Definitia 1.1. O functie x : [0,T ) 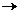 X se numeste solutie clasica pentru sistemul (S) daca
indeplineste urmatoarele conditii :
X se numeste solutie clasica pentru sistemul (S) daca
indeplineste urmatoarele conditii :
(i) x
este continua pe [ 0, T)
si de clasa 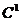 pe ( 0, T);
pe ( 0, T);
(ii) x(t)
 D(A) , pentru orice
D(A) , pentru orice 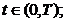
(iii) x verifica sistemul (S).
Fie
p  [ 1,
[ 1,  ) , a, b
) , a, b  R , a
< b. Consideram spatiul liniar
R , a
< b. Consideram spatiul liniar 
al functiilor f : [a , b] 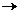 X
masurabile Bochner cu proprietatea ca
X
masurabile Bochner cu proprietatea ca 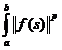 ds <
ds <  , care este
spatiul Banach in raport
cu norma
, care este
spatiul Banach in raport
cu norma
 .
.
Similar consideram spatiul liniar L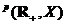 al functiilor f :
al functiilor f : 
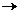 X masurabile Bochner cu
X masurabile Bochner cu 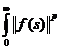 ds <
ds <  , care este spatiu Banach in raport cu norma
, care este spatiu Banach in raport cu norma
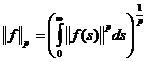 .
.
Definitia
1.2. Fie T 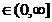 si f : [0,T)
si f : [0,T) 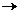 X o functie masurabila f se zice local masurabila si notam f
X o functie masurabila f se zice local masurabila si notam f 
 daca pentru orice t
daca pentru orice t  (0 ,T )
avem
(0 ,T )
avem
f 
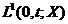 .
.
In continuare , vom studia solutiile
sistemului (S) in ipoteza ca f 
 .
.
Teorema 1.1. Daca x este solutie pentru sistemul (S), atunci
x(t) = S(t)x +
+ 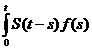 ds,
ds,  .
.
Demonstratie . Fie t  (0,T). Consideram
functia
(0,T). Consideram
functia
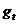 : [0,t]
: [0,t] 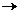 X , g
X , g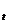 (s) = S(
(s) = S( )x(s) .
)x(s) .
Atunci g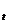 este derivabila pe (0,t) si avem ca
este derivabila pe (0,t) si avem ca
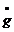 (s)=
(s)=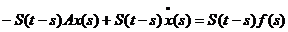 ,
,  .
.
Integrand pe [0,t] rezulta ca
 ds = g
ds = g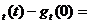 x(t)
x(t)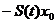
care incheie demonstratia .
Corolarul
1.1. Sistemul (S) are cel mult o
solutie clasica.
Demonstratie.
Se obtine imediat
din Teorema 1.1.
Reprezentarea
solutiei clasice data de Teorema 1.1. permite introducerea unui alt
concept de solutie pentru problema Cauchy neomogena.
Definitia
1.3. Fie 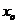

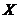 si f
si f 
 . Functia x : [0,T)
. Functia x : [0,T) 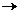 X
X
data de relatia
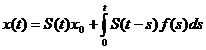 ,
, 
se numeste solutie moderata
(mild) a sistemului (S).
Teorema urmatoare ne da o
proprietate importanta a solutiei moderate.
Teorema 1.2. Daca x : [0,T) 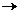 X este solutia moderata a sistemului (S)
atunci x este continua pe [0,T
X este solutia moderata a sistemului (S)
atunci x este continua pe [0,T
Demonstratie. Fie t 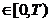 si
si 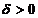 astfel incat t +
astfel incat t +  < T . Pentru h
< T . Pentru h  [0,
[0,  ) avem ca
) avem ca
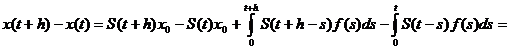
 (2.1)
(2.1)
Avand
in vedere ca 
ramane sa demonstram ca
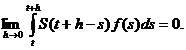 (2.2)
(2.2)
Fie ( )
) 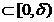 cu
cu  . Pentru fiecare n
. Pentru fiecare n  , consideram
functia
, consideram
functia
 ,
, 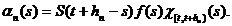
Atunci 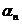 este
masurabila si
este
masurabila si 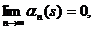 pentru orice
pentru orice 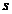

 .
.
Daca M
,  sunt dati de Teorema I.1.1 pentru S , deducem ca
sunt dati de Teorema I.1.1 pentru S , deducem ca
 ,
, 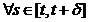 .
.
Cum f 
 rezulta
ca f
rezulta
ca f 
 . Din teorema
convergentei dominate a lui Lebesgue , deducem ca
. Din teorema
convergentei dominate a lui Lebesgue , deducem ca
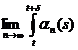 ds
ds
Dar
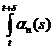 ds =
ds =  ds ,
ds , 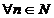 .
.
Rezulta ca
 ds
ds  , pentru
, pentru 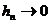 ,
,
si atunci din Teorema
lui Heine se obtine relatia (2.2) . Astfel , tinand seama de
relatia (2.2) si trecand la limita in relatia (2.1) deducem ca x este continua la dreapta in t .
Fie t > 0 si  > 0 astfel
incat
> 0 astfel
incat 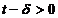 . Pentru
. Pentru 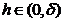 avem
avem





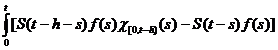 ds. (2.3)
ds. (2.3)
Fie ( )
) 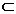 [0,
[0, ) cu
) cu  . Pentru fiecare
. Pentru fiecare  , consideram
functia
, consideram
functia

 .
.
Atunci ,  este
masurabila si
este
masurabila si  = 0 , pentru orice
= 0 , pentru orice  . In plus
avem ca
. In plus
avem ca
 ,
, 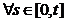 .
.
Din f 
 deducem
ca f
deducem
ca f 
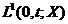 . Din teorema convergentei dominate a lui Lebesgue ,
obtinem ca
. Din teorema convergentei dominate a lui Lebesgue ,
obtinem ca
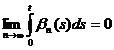 .
.
De aici si din Teorema lui Heine rezulta
ca
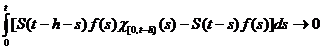 , pentru
, pentru 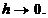 (2.4)
(2.4)
Din (2.3) si (2.4) avem ca x este continua la stanga in t . Deci x este continua pe [0,T
2 Conditii necesare ca o solutie
moderata sa fie clasica
Remarca 2.1. In general , chiar daca f este continua pe [0,T) , nu rezulta ca solutia moderata este
solutia clasica.
Exemplul
2.1. Fie 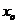

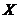 cu proprietatea
ca S(t)
cu proprietatea
ca S(t)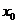
 D(A) , pentru
orice
D(A) , pentru
orice 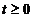 . Consideram sistemul
. Consideram sistemul
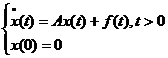
unde f(t) = S(t)x , pentru orice t > 0. Atunci avem ca f este continua pe
, pentru orice t > 0. Atunci avem ca f este continua pe  si x(0) =
0
si x(0) =
0  D(A). Cu toate
acestea , solutia moderata are expresia
D(A). Cu toate
acestea , solutia moderata are expresia
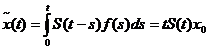 ,
,  ,
,
deci 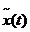
 D(A), pentru orice t > 0 .
D(A), pentru orice t > 0 .
Rezulta ca solutia moderata nu este solutie
clasica . Conform Teoremei 1.1. , obtinem de aici ca sisteml (S) nu are solutie clasica .
Are sens sa ne punem urmatoarea
intrebare :
Problema : In ce conditii solutia mild este
solutie clasica ?
Teorema
2.2. Fie
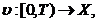
 ds .
ds .
Daca x 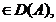 f este continua
pe [0,T) si
f este continua
pe [0,T) si  este o aplicatie
de clasa C
este o aplicatie
de clasa C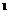 pe (0,T), atunci solutia moderata a sistemului (S) este
solutia clasica.
pe (0,T), atunci solutia moderata a sistemului (S) este
solutia clasica.
Demonstratie.
Fie x solutia moderata a sistemului (S) , care
conform Teoremei 1.2 este continua . Fie
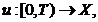 u(t)=S(t)x
u(t)=S(t)x .
.
Rezulta
ca
x(t)=u(t)+v(t), 
Din 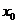
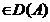 avem ca u este
de clasa
avem ca u este
de clasa 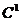 pe
pe  Tinand seama de ipoteza deducem
ca x este de clasa
Tinand seama de ipoteza deducem
ca x este de clasa 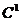 pe (0,T). In plus,
din x
pe (0,T). In plus,
din x
 D(A) obtinem
ca u(t)
D(A) obtinem
ca u(t)  D(A), pentru orice
t
D(A), pentru orice
t  (0,T).
(0,T).
Aratam ca v(t)  D(A), pentru orice
t
D(A), pentru orice
t  (0,T).
(0,T).
Fie t  (0,T). Avem
succesiv ca
(0,T). Avem
succesiv ca

 (2.5)
(2.5)
Demonstram ca
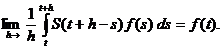 (2.6)
(2.6)
Fie
M, > 0, dati de Teorema I.1.1. pentru S. Fie
> 0, dati de Teorema I.1.1. pentru S. Fie 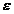 > 0. Din f continua pe [0,T) exista
> 0. Din f continua pe [0,T) exista 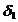 > 0 astfel incat
> 0 astfel incat

Din 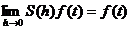 exista
exista 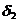 > 0 astfel incat
> 0 astfel incat

Fie 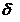 = min . Pentru
= min . Pentru 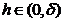 avem ca
avem ca


+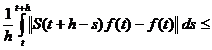
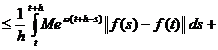
+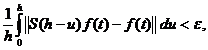
de unde obtinem
relatia (2.6). Atunci , din (2.5) si (2.6) si ipoteza
rezulta
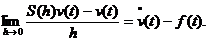
Deci , v(t) 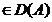 si
si
Av(t) 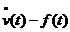 ,
, 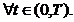
Deducem de aici ca x(t)  D(A), pentru orice
t
D(A), pentru orice
t .
.
Din
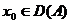 avem ca
avem ca
 .
.
Atunci , rezulta ca

In plus , x(0)=u(0)+v(0)=x , deci x verifica sistemul (S).
, deci x verifica sistemul (S).
Teorema 2.3. Daca x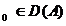 si f este o functie de clasa
si f este o functie de clasa 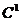 pe [0,T),
atunci sistemul (S) are o unica solutie classica.
pe [0,T),
atunci sistemul (S) are o unica solutie classica.
Demonstratie. Conform Teoremei 2.2. este suficient sa
demonstram ca functia
v : [0,T)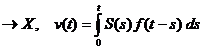
este de clasa 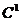 pe (0,T).
pe (0,T).
Fie t >0 . Avem succesiv ca

+
Reluand
rationamentul facut in demonstratia Teoremei 1.3. si
tinand seama de faptul ca f
este continua, obtinem
ca
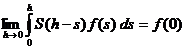
de unde deducem
ca

=S(t)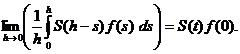
Ramane sa
aratam ca
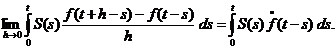 (2.9)
(2.9)
Fie 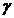 > 0 astfel
incat
> 0 astfel
incat 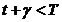 si (
si (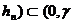 ) cu
) cu 
Pentru
fiecare  consideram
functia
consideram
functia

Atunci 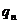 este
masurabila si
este
masurabila si  pentru orice
pentru orice  .
.
Fie  si
si 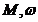 dati de Teorema I.1.1.
pentru S.
dati de Teorema I.1.1.
pentru S.
Pentru fiecare  si fiecare
si fiecare  exista
exista  astfel incat
astfel incat
 .
.

Rezulta
ca
 ,
,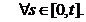
Din teorema
convergentei dominate a lui Lebesgue deducem ca
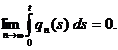
Atunci din
teorema lui Heine obtinem ca exista

Procedand in mod
analog obtinem ca
 .
.
Rezulta ca v este
derivabila pe (0,T) si
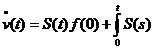
 ds.e de
clasa
ds.e de
clasa
Cum f
este de clasa 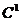 pe [0,T) deducem de mai sus ca
pe [0,T) deducem de mai sus ca  este continua pe
[0,T), deci v este de clasa
este continua pe
[0,T), deci v este de clasa 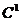 pe (0,T).Din
Teorema 2.3. si Corolarul 1.1. concluzionam ca sistemul (S)
are o unica solutie clasica.
pe (0,T).Din
Teorema 2.3. si Corolarul 1.1. concluzionam ca sistemul (S)
are o unica solutie clasica.



Bibliografie
1. Buse, C. - Comportari asimptotice ale proceselor de
evolutie, Editura Sedona, Timisoara,
1988;
2. Cristescu, K. - Analiza functionala, Editura
Didactica ;
3. Curtain, R; Zwart, H. J. - An Introduction to Infinite
Dimensional Linear Control
Systems Theory, Springer Verlag
, New York,
1995 ;
4. Curtain, R; Pritchard, A.J. - Functional Analysis in Modern
Applied Mathematics, Mathematics in
Science and Engineering 132, Academic Press 1977;
5. Engel , K. J.; Nagel, R. - One- Parameter Semigroups for Linear
Evolution Equations, Graduate Texts in Mathematics, vol 194, Berlin 2000;
6. Gaspar, D.- Analiza functionala, Editura
Facla, Timisoara
1981;
7. Hille, E; Phillips , R. S. - Functional Analysis and Semi-groups
American Mathematical Society, Colloquium Publications Vol 31, Providence, R.
I. 1957;
8. Gheorghiu, N.- Introducere in analiza functionala,
Editura Academiei RSR, Bucuresti 1974;
9. von Neerven, J. M. A. M.- The Asymptotic Behaviour of Semigroups of Linear Operators, Operator
Theory Advanced and Applications, vol 88, Birkhäuser, Bassel 1996;
10. Pazy, A. - Semigroups of Linear Operators and Applications to
Partial Differential Equations, Springer Verlag, 1983;
11. Sasu, A. L. . Sasu, B.- Sisteme liniare cu control, Editura
Politehnica Timisoara 2003;
12. Yosida, K- Functional Analysis, Springer Verlag, 1993.




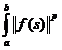 ds
ds  .
.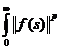 ds <
ds < 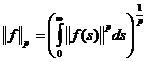 .
.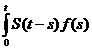 ds,
ds,  ds
ds 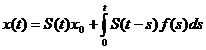 ,
, 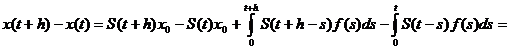


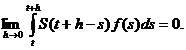
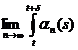 ds
ds 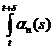 ds =
ds =  ds ,
ds , 

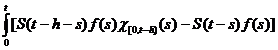 ds. (2.3)
ds. (2.3)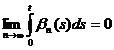 .
.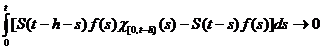 , pentru
, pentru 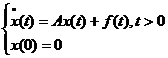
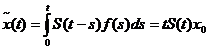 ,
, ds .
ds .

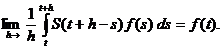


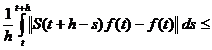
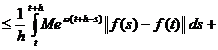
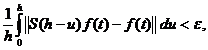
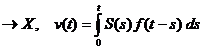


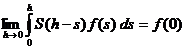

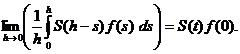
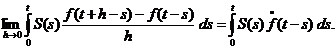

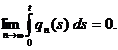

 .
.