Reprezentarea vectorilor in plan
Reprezentarea numerelor prin puncte pe axa este puntea care
leaga algebra de geometri
Se
numeste axa de coordonare o dreapta pe care sunt fixate :un punct o numit origine), un segment oe a carui
lungime este egala cu unitatea si un
sens pozitiv
X' A(-3) 0o A(4) x
Axa ox
are punctul pozitiv de la o la x indicat de sageata (x si x' indica sensurile
si nu sunt pe axa ) sensul contrar celui pozitiv este sensul negativ .Am invatat ca oricarui
punct a de pe axa i corespunde un numar
real unic abscisa sau coordonata
punctului A si reciproc , oricarui numar real a i corespunde un singur punct A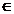 Ox imagine
alui a
Ox imagine
alui a
Exemplu
Fie A(x1)
si A2 (x2) pe axa Ox .Abscisa mijlocului segmentului A1A2 este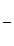
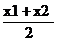
Cele
doua coordonate care determina pozitia
unui punct in plan sunt numite
carteziene dupa numele latinizat al
matematicianului si filozofului francez Descartes (1596-1650). Aceste
coordonate au fost folosite prima data de Nicolae d'Orseme
(1325-1382), cu 260 de ani inaintea lui Descartes . Se spune ca descartes a inventat coordonatele carteziene in timp ce urmarea o
musca pe tavan .In acel moment i-a venit ideea ca ca putea repera musca prin distantele de la musca la dreptele care
marginesc tavabul .Descarte si Fermat au utilizat reperele carteziene pentru a
descrie curbe plane cu ajutorul ecuatiilor .
Definitie
;
Se numeste reper cartezian in
plan un sistem format din doua axe Ox si Oy cu aceeasi origine .Un reper cartezian format
di axele Ox si Oy il notam Oy .Daca axele Ox si Oy sunt perpendiculare xOy se numeste reper
ortogonal (sistem ortogonal)
Teorema :
Intr-un reper cartizan ,
orcarui punct M din plan i corespunde unui singur vector (a,b) 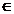 R
R 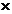 R=R2 ce
reprezinata coordonatele sale si , reciproc pentru orice
vector (a,b)
R=R2 ce
reprezinata coordonatele sale si , reciproc pentru orice
vector (a,b) 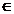 R2 exista
un unic punct M(a, b)
R2 exista
un unic punct M(a, b)
Demonstratie Fie (a,b) un vector .Intrun reper
cartezian xOy notam cu n punctul de pe Ox de
coordonata a si cu p punctul de pe Oy de
coordonata b.Fie M punctul de intersectie dintre perpendiculara in N pe Ox si perpendiculara in p si Oy
Am asociat vectorului (a, b) un unic punct M din plan .Reciproc
unui punct m din plan i se asociaza vectorul (a,b) , unde a si b sunt coordonatele proiectilor lui m si Ox
si O y









 y
y
II I

 P(O,Y) m(x,y_
P(O,Y) m(x,y_
X' x
0
III IV
y'
Definitie :
Un reper cartezian determina o impartiere a planului in
patru regiuni numite cadrane marcate cu cifre romane I ,II ,III, IV si definite astfel


 I= II=
I= II=

 III= IV={M(x,y) x>0 ,y<0
III= IV={M(x,y) x>0 ,y<0
Teorema Daca M (x1 y1) si M2(x 1 y2 )
puncte in plan atunci M1M2
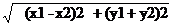
Aceasta egalitate
reprezinata formula distantei
dintre punctele M (x1
y1) si M2(x 1 y2 )
Exemplu
Fie punctele M1,2) di n(-3-3)












 Atunci MN
Atunci MN 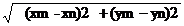 =5
=5
y


 -3 -1 M(Xm'
-Ym )x
-3 -1 M(Xm'
-Ym )x
0
N(Xm' -Ym
Fie punctele A(x1 ,y1)
si A2(x2 ,y2)
si M mijlocul segmentului A1
A2 .
Arata ca m are coordonatele Xm=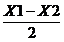 Ym=
Ym=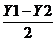
Notam cu B1(x1)
si B2 (x2) proportile punctelor A1 A2
pe ox .Mijlocul segmentului B1B2 este punctul n 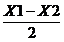 ,0
,0
Deoarece A1 B1 MN A2 B2 rezulta ca abcisa lui m este si abscisa lui n adica Xm =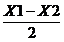 .analog obtinem ca
Ym=
.analog obtinem ca
Ym=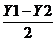






































 C2(O,y2)
C2(O,y2)
A(x2,y2)
P(0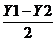 ) M . C1 (0,y1) A(x1, y1)
) M . C1 (0,y1) A(x1, y1)
x
0 B1(x1 ,O)N 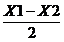 ,0 B(X20)
,0 B(X20)



