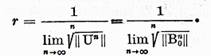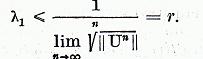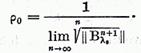Rezolventa
Vom continua aici studiul ecuatiei
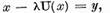 (1)
(1)
totusi spre deosebire de paragraful precedent ne va interesa acum
cazul in care ea admite o solutie unica.
Fie 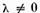 o valoare nesingulara a operatorului U.
Operatorul
o valoare nesingulara a operatorului U.
Operatorul 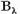 definit din relatia
definit din relatia
 (2)
(2)
se numeste rezolventa operatorului U. Pentru 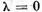 vom pune
vom pune 
Daca se are in vedere spectrul si respectiv multimea
valorilor regulate atunci in locul lui  este mai comod sa se considere operatorul
este mai comod sa se considere operatorul
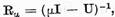 (3)
(3)
care are sens pentru toate valorile regulate ale operatorului U. Operatorul
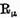 va fi numit tot rezolventa. Pericolul de
confuzie a celor doua notiuni este exlus deoarece va fi intotdeauna
clar din context despre care dintre rezolvente este vorba; in afara de
aceasta cele doua rezolvente pot fi distinse prin faptul ca sunt
notate in mod diferit. Sa remarcam ca rezolventa
va fi numit tot rezolventa. Pericolul de
confuzie a celor doua notiuni este exlus deoarece va fi intotdeauna
clar din context despre care dintre rezolvente este vorba; in afara de
aceasta cele doua rezolvente pot fi distinse prin faptul ca sunt
notate in mod diferit. Sa remarcam ca rezolventa  se
intalneste adesea in teoria ecuatiilor integrale , unde este
numita rezolventa Freedholm pe cand in teoria in analiza
functionala prin rezolventa se intelege de obicei
se
intalneste adesea in teoria ecuatiilor integrale , unde este
numita rezolventa Freedholm pe cand in teoria in analiza
functionala prin rezolventa se intelege de obicei  .
.
Daca 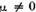 evident
evident

Invers din egalitatea
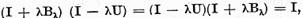
obtinem

Prin urmare pentru 

Relatiile (4) si (6) permit reformularea pentru 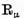 a tuturor propozitiilor demonstrate
pentru
a tuturor propozitiilor demonstrate
pentru  si reciproc
si reciproc
Sa
studiem comportarea rezolventei 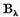 pentru
pentru 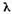 mici. Sa consideram seria
mici. Sa consideram seria
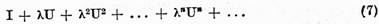
Daca seria converge in spatiul de operatori B
(X,X) atunci conform
observatiei la teorema lui Banach suma ei este  adica
adica

de unde ca urmare a relatiei (5)
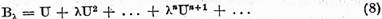
Aceasta formula are loc pentru acele valori ale lui  pentru care seria (7) converge daca
pentru care seria (7) converge daca

si diverge daca

Ajungem astfel la teorema urmatoare.
Teorema III.3.1. Rezolventa
 admite dezvoltarea (8) in serie dupa
puterile lui
admite dezvoltarea (8) in serie dupa
puterile lui  a carei raza de
convergenta este
a carei raza de
convergenta este
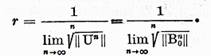
Daca trecem cu ajutorul relatiilor (4) de la rezolventa  la rezolventa
la rezolventa  obtinem :
obtinem :
Corolar. Rezolventa  admite dezvoltarea in serie dupa puterile
lui
admite dezvoltarea in serie dupa puterile
lui 

Raza de convergenta a seriei (8)
poate fi exprimata si in functie de localizarea multimii
caracteristice in planul complex.
Vom demonstra mai intai doua propozitii ajutatoare.
Lema III.3.2. Pentru
orice  are loc egalitatea
are loc egalitatea

Demonstratie. Din relatia (5) avem
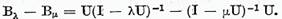
Inmultind la dreapta aceasta egalitate cu  si apoi la stanga cu
si apoi la stanga cu 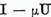 obtinem
obtinem

si prin urmare

ceea ce trebuie demonstrat.
Corolar. Operatorii  comuta, adica
comuta, adica 
Se demonstreaza analog ca pentru toti 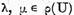

Lema III.3.3. Rezolventa
 este functie
continua de parametrul
este functie
continua de parametrul 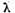 in orice punct al multimii
in orice punct al multimii  adica daca
adica daca  atunci
atunci 
Demonstratie. Vom demonstra intai ca functia
reala  este continua pe
este continua pe  . Daca U =0,
atunci
. Daca U =0,
atunci 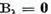 si afirmatia este demonstrata.
Daca
si afirmatia este demonstrata.
Daca  atunci
atunci  ceea ce permite demonstrarea continuitatii
functiei
ceea ce permite demonstrarea continuitatii
functiei  .
.
Din (9) obtinem
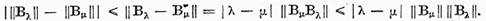
Prin urmare
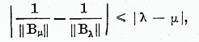
de unde obtinem rezultatul dorit.
Sa stabilim acum continuitatea lui 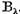 . Deoarece
multimea
. Deoarece
multimea 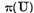 este deschisa , iar
este deschisa , iar  exista un disc
exista un disc  continut in intregime in
continut in intregime in 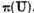 . Functia
continua
. Functia
continua  este marginita pe acest disc, fie de
exemplu
este marginita pe acest disc, fie de
exemplu
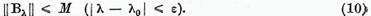
Conform relatiilor (9) si (10) ,

lema este astfel demonstrata.
Teorema III.3.4. Raza
de convergenta r a seriei (8) este egala cu distanta  de la punctul
de la punctul  la multimea caracteristica
la multimea caracteristica 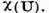
Demonstratie. In primul rand, deoarece discul  converge si prin urmare , pentru
acesti
converge si prin urmare , pentru
acesti 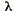 rezolvanta exista, discul respectiv este
continut in multimea valorilor nesingulare. De aceea
rezolvanta exista, discul respectiv este
continut in multimea valorilor nesingulare. De aceea 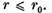
Sa luam acum un element arbitrar  si o functie arbitrara
si o functie arbitrara 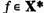 si sa consideram functia
si sa consideram functia  de variabila complexa
de variabila complexa 
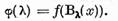
Sa demonstram ca  este regulata pe multimea
este regulata pe multimea 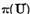 . Intradevar
daca
. Intradevar
daca  atunci in virtutea relatiei (9)
atunci in virtutea relatiei (9)

Cand  membrul drept are limita
membrul drept are limita 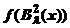 (lema III.3.3).Astfel
exista derivata continua
(lema III.3.3).Astfel
exista derivata continua

Sa dezvoltam functia  in seria Taylor in vecinatatea punctului
in seria Taylor in vecinatatea punctului 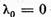

Aceasta dezvoltare are sens in orice disc care nu contine puncte
singulare ale lui 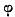 si deci cu atat mai mult in discul
si deci cu atat mai mult in discul 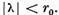 Deoarece in virtutea relatiei (8)
Deoarece in virtutea relatiei (8)

In plus ca urmare a cunoscutei teoreme din teoria functiilor de
variabila complexa , seriile  coincid astfel incat seria (12) converge
pentru
coincid astfel incat seria (12) converge
pentru 
Sa luam  arbitrar. Din convergenta seriei (12)
pentru
arbitrar. Din convergenta seriei (12)
pentru 
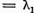 rezulta ca
rezulta ca
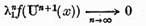
si prin urmare , deoarece f este arbitrara
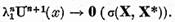
Dar un sir slab convergent este marginit

Deoarece aceasta inegalitate este indeplinita pentru orice 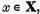 iar spatiul X este complet, atunci
iar spatiul X este complet, atunci

De aceea

si
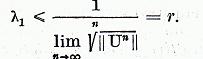
Deoarece  poate fi luata arbitrar de aproape de
poate fi luata arbitrar de aproape de  . Tinand seama
si de inegalitatea
. Tinand seama
si de inegalitatea  ,
demonstrata mai sus obtinem de aici
,
demonstrata mai sus obtinem de aici  ceea ce trebuie demonstrat
ceea ce trebuie demonstrat
Observatie Fie
 o valoare nesingulara a operatorului U. Ca si mai sus se poate observa
dezvoltarea
o valoare nesingulara a operatorului U. Ca si mai sus se poate observa
dezvoltarea

care are loc in discul  unde
unde 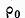 este distanta de la punctul
este distanta de la punctul 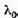 pana la multime caracteristica
sau, ca si in teorema III.3.1
pana la multime caracteristica
sau, ca si in teorema III.3.1
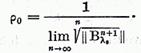
Inlocuind rezolvanta  prin rezolvanta
prin rezolvanta 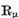 obtinem urmatorul rezultat.
obtinem urmatorul rezultat.
Corolar .
Dezvoltarea

are loc pentru 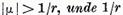 este raza celui mai mic disc cu centrul in
origine care contine in intregime spectrul.
este raza celui mai mic disc cu centrul in
origine care contine in intregime spectrul.
Numarul 1/r se
numeste raza spectrala a operatorului U.
Observatie Daca U
este un operator autodjunct in spatiul Hilbert atunci 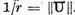 Impreuna cu rezultatul corolarului la teorema
III.3.1 aceasta ne conduce la relatia interesanta
Impreuna cu rezultatul corolarului la teorema
III.3.1 aceasta ne conduce la relatia interesanta
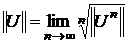
Corolar Spectrul  al unui operator liniar continuu U intr-un spatiul Banach complex,
nevid.
al unui operator liniar continuu U intr-un spatiul Banach complex,
nevid.
Demonstratie. Daca 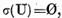 atunci luand in considerare legatura intre
atunci luand in considerare legatura intre  obtinem ca multimea
obtinem ca multimea 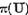 a valorilor nesingulare este intreg planul
complex. Deoarece putem considera
a valorilor nesingulare este intreg planul
complex. Deoarece putem considera 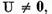 avem pentru orice
avem pentru orice  operatorul
operatorul 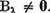 . Fie
. Fie  Sa luam
Sa luam 
 .
.
Analog cu demonstratia teoremei III.3.4 obtinem functia

este regulata in tot planul complex
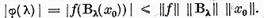
Deoarece 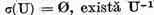 continuu de unde obtinem ca in lema III.3.3
ca pentru
continuu de unde obtinem ca in lema III.3.3
ca pentru  Prin urmare in
virtutea relatiei(6),
Prin urmare in
virtutea relatiei(6),

Asadar  este marginita, de unde conform
teoriei lui Liouville
este marginita, de unde conform
teoriei lui Liouville  este identic egala cu o constanta
care evident nu poate fi decat zero. Totusi
este identic egala cu o constanta
care evident nu poate fi decat zero. Totusi  contradictia obtinuta demonstreaza
corolarul.
contradictia obtinuta demonstreaza
corolarul.
Sa remarcam ca daca am fi incercat sa definim
spectrul unui operator U intr-un
spatiu real intr-un mod analog celui
folosit la punctul III.1. spectrul ar fi putut fi multimea vida.
Aceasta este principala cauza pentru care consideram cazul complex.