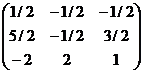|
Orice spatiu
vectorial nenul admite o baza. Daca numarul vectorilor dintr-o baza este
finit, atunci spatiul vectorial se numeste finit dimensional.
Fie B=
o baza in V si 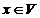 un vector. In raport cu baza B, vectorul x se scrie
in mod unic x= a1x1+.+anxn.
cu un vector. In raport cu baza B, vectorul x se scrie
in mod unic x= a1x1+.+anxn.
cu 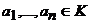 . Elementele . Elementele 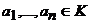 se numesc coordonatele vectorului x in raport
cu baza B si sunt unic determinate in raport cu aceasta baza. se numesc coordonatele vectorului x in raport
cu baza B si sunt unic determinate in raport cu aceasta baza.
Fie V
un spatiu vectorial peste un corp comutativ K, B1= si B2=
doua baze in V. Fie 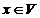 un vector si un vector si 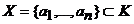 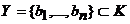 coordonatele vectorului x fata de baza B1,
respectiv B2. coordonatele vectorului x fata de baza B1,
respectiv B2.
Exprimam
vectorii din baza B2 in
functie de vectorii din baza B1.
Coordonatele astfel obtinute se vor trece, in ordine, pe coloane, obtinand
matricea de trecere de la baza B1
la baza B2, pe care o
notam cu A. Legatura dintre A, X si Y este data de formula
X=AY
numita si formula modificarii coordonatelor la schimbarea
bazei.
Exemplu. Fie B1=
si B2= doua baze in V=R3, e1=(1, 2, 3), e2=(1,
0, 1), e3=(1, 1, 1), f1=(1, -1, 2), f2=(1, 1, 0), f3=(2, 0, 1) si v=(1, -1, 4). Sa se scrie matricea A de trecere de la baza B1 la baza B2 si sa se determine formula schimbarii de coordonate pentru vectorul v
la schimbarea bazei.
Rezolvare. Determinam mai intai
coordonatele vectorului v fata de bazele B1 si B2. Fata de baza B1 avem v= a1e1+a2e2+a3e3.
Rezulta sistemul 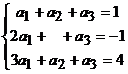 . Solutia acestui sistem este: a1=3/2, a2=7/2, a3=-4. Deci X 3/2, 7/2, -4). . Solutia acestui sistem este: a1=3/2, a2=7/2, a3=-4. Deci X 3/2, 7/2, -4).
Fata de baza B2 avem v= b1e1+b2e2+b3e3.
Rezulta sistemul 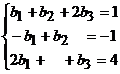 . Solutia acestui sistem este: b1=3, b2=2, b3=-2. Deci Y 3, 2, -2). . Solutia acestui sistem este: b1=3, b2=2, b3=-2. Deci Y 3, 2, -2).
Determinam matricea de trecere de la baza B1
la baza B2. Scriem f1=a1e1+a2e2+a3e3.
Obtinem sistemul 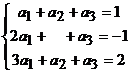 , cu solutia (1/2, 5/2, -2), care reprezinta prima coloana
a matricei de trecere de la baza B1 la baza B2. , cu solutia (1/2, 5/2, -2), care reprezinta prima coloana
a matricei de trecere de la baza B1 la baza B2.
Scriem f2=b1e1+b2e2+b3e3.
Obtinem sistemul 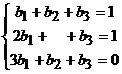 , cu solutia (-1/2, -1/2, 2), care reprezinta a doua coloana a matricei de trecere de la baza B1
la baza B2. Scriem f3=c1e1+c2e2+c3e3.
Obtinem sistemul , cu solutia (-1/2, -1/2, 2), care reprezinta a doua coloana a matricei de trecere de la baza B1
la baza B2. Scriem f3=c1e1+c2e2+c3e3.
Obtinem sistemul 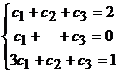 , cu solutia (-1/2, 3/2, 1), care reprezinta a treia coloana a matricei de trecere de la baza B1 la baza B2.
Deci
matricea A este: , cu solutia (-1/2, 3/2, 1), care reprezinta a treia coloana a matricei de trecere de la baza B1 la baza B2.
Deci
matricea A este: 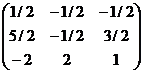
Cum v=3f1+2f2-2f3
in baza B2, avem coordonatele in baza B1 astfel
a1
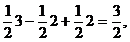 a2= a2=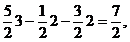 a3 = a3 =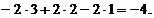
|


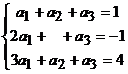 . Solutia acestui sistem este: a1=3/2, a2=7/2, a3=-4. Deci X 3/2, 7/2, -4).
. Solutia acestui sistem este: a1=3/2, a2=7/2, a3=-4. Deci X 3/2, 7/2, -4).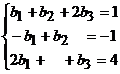 . Solutia acestui sistem este: b1=3, b2=2, b3=-2. Deci Y 3, 2, -2).
. Solutia acestui sistem este: b1=3, b2=2, b3=-2. Deci Y 3, 2, -2). 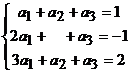 , cu solutia (1/2, 5/2, -2), care reprezinta prima coloana
a matricei de trecere de la baza B1 la baza B2.
, cu solutia (1/2, 5/2, -2), care reprezinta prima coloana
a matricei de trecere de la baza B1 la baza B2.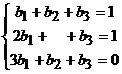 , cu solutia (-1/2, -1/2, 2), care reprezinta a doua coloana a matricei de trecere de la baza B1
la baza B2. Scriem f3=c1e1+c2e2+c3e3.
Obtinem sistemul
, cu solutia (-1/2, -1/2, 2), care reprezinta a doua coloana a matricei de trecere de la baza B1
la baza B2. Scriem f3=c1e1+c2e2+c3e3.
Obtinem sistemul 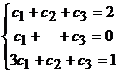 , cu solutia (-1/2, 3/2, 1), care reprezinta a treia coloana a matricei de trecere de la baza B1 la baza B2.
, cu solutia (-1/2, 3/2, 1), care reprezinta a treia coloana a matricei de trecere de la baza B1 la baza B2.