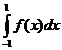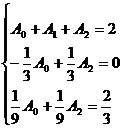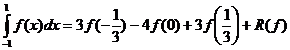Calculul integralelor definite
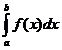
cu
ajutorul formulei Leibnitz-Newton, presupune cunoașterea unei primitive a
funcției f. In foarte multe cazuri calculul primitivelor este foarte
complicat (uneori imposibil) și nu pot fi obținute prin metode
elementare.
Uneori in practica,
funcția f nu este cunoscuta sub forma analitica, ci se
cunosc valorile sale intr-o rețea de puncte .
In aceste cazuri problema
determinarii unei primitive nu mai are sens.
Din aceste motive
metodele numerice de aproximare a integralelor au o deosebita
importanța.
Voi
incepe cu formulele de calcul numeric pentru integralele simple. Procedeul
folosit pentru determinarea formulelor de calcul numeric consta in
inlocuirea funcției date f printr-o funcție de aproximare g, pentru
care se pot calcula primitive. Daca funcția f se cunoaște
analitic, atunci se poate evalua și eroarea de aproximare:
R(f)=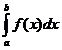
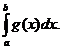
Voi prezenta in
continuare o metoda de deducere a unor formule de integrare numerica
folosind polinoamele de interpolare.
Sa
presupunem ca se cunosc valorile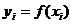
 , in punctele x
, in punctele x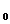 ,x
,x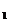 ,,x
,,x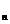
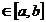
In acest caz, in rolul funcției g
putem lua polinomul de interpolare al lui Lagrange:
L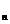 (x)=
(x)=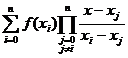
Obținem
formula de calcul:
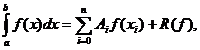
unde
A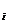
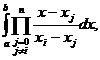
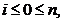
iar R(f) este eroarea de
aproximare (restul).
Daca
limitele de integrare a și b sunt puncte de interpolare, formula (4) se
numește formula de integrare numerica de tip inchis. In caz
contrar, se numește formula de integrare numerica de tip
deschis.
Pentru calculul coeficienților A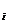 observam ca:
observam ca:
numerele A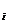 nu depind de funcția f;
nu depind de funcția f;
pentru polinoame de grad cel mult n, formula (4) este exacta
(R(f)=0), deoarece in acest caz L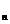 =f.
=f.
Pentru
f(x)= x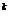
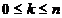 in (4)
avem R(f)=0. Obținem:
in (4)
avem R(f)=0. Obținem:
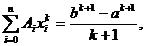
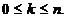
Acest sistem este liniar neomogen, cu n+1
ecuații și n+1 necunoscute: A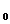 ,A
,A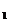 ,,A
,,A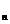 .
.
Determinantul acestui sistem este:
D=
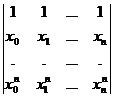 =
=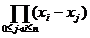
Nodurile fiind distincte, rezulta D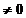 . Așadar, numerele A
. Așadar, numerele A ,A
,A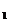 ,,A
,,A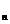 sunt unic determinate.
sunt unic determinate.
Aceasta
metoda de integrare numerica nu presupune calculul efectiv al
polinomului de interpolare al lui Lagrange.
Exemplu. Sa se deduca formula (4) pentru 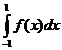 cu n=2, x
cu n=2, x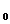
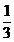 , x
, x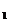 =0, x
=0, x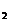
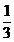
Soluție. Sistemul (6) este in acest caz urmatorul:
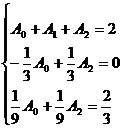
Acest sistem are soluția: A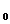 =A
=A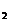 =3, A
=3, A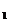 =-4.
=-4.
Rezulta
formula:
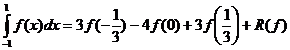
Formula (7) este
de tip deschis și este exacta pentru polinoame de grad cel mult doi.
Se observa ușor ca aceasta formula este exacta
și pentru polinoame de gradul trei (pentru f(x)=x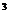 ambii membri sunt nuli) .
ambii membri sunt nuli) .


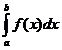
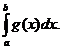
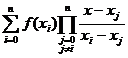
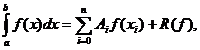
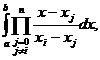
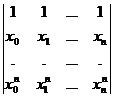 =
=