Sisteme
cuantice unidimensinale
Vom
studia miscarea unei particule de masa m in care se deplaseaza
pe axa ox intr-un potential V(x) . Ecuatia sa Schrodinger este :
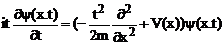
In cazul
stationar in care energia sistemului este E , functia de unda
este :
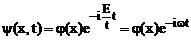
unde 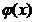 satisface ecuatia
Schrodiger atemporala :
satisface ecuatia
Schrodiger atemporala :
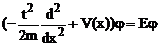
Vom studia mai intai cazul unei particule libere V(x)=constant
1. Particula libera
In
absenta fortelor exterioare energia potentiala este o
constanta pe care o putem alege zero . Ecuatia Schrodinger
atemporala devine :
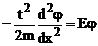 sau
sau

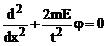
 Energia particulei libere fiind pozitiva , putem nota
Energia particulei libere fiind pozitiva , putem nota 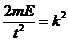 si ecuatia
devine :
si ecuatia
devine :

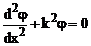 Aceasta
ecuatie are ca solutii liniar independente
Aceasta
ecuatie are ca solutii liniar independente 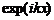 si
si 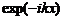 sau, echivalent,
perechea de solutii reale
sau, echivalent,
perechea de solutii reale 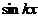 si
si 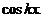 Solutia
generala a ecuatiei va fi:
Solutia
generala a ecuatiei va fi:
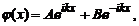
unde A si B
sunt constante arbitrare.
Functia de unda ; 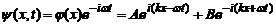 , este suma a doi termeni dintre care primul exprima o
unda plana alergand in sensul pozitiv al axei x (cu
amplitudinea A, pulsatia
, este suma a doi termeni dintre care primul exprima o
unda plana alergand in sensul pozitiv al axei x (cu
amplitudinea A, pulsatia 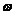 si vectorul de
unda
si vectorul de
unda 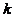 ), iar al doilea, o unda plana regresiva, care
se deplaseaza in sensul opus al axei ox. Calculand densitatea de
probabilitate P si j-densitatea de curent de probabilitate,
obtinem :
), iar al doilea, o unda plana regresiva, care
se deplaseaza in sensul opus al axei ox. Calculand densitatea de
probabilitate P si j-densitatea de curent de probabilitate,
obtinem :
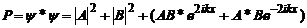 si
si 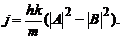
Densitatea de probabilitate
arata interferenta a doua unde concurente care determinata o
periodicitate spatiala iar densitatea de curent este diferenta
intre doi curenti de probabilitate opusi.
In cazul 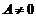 si
si 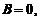 unda plana
monocromatica progresiva descrie o particula care se
misca in sensul axei x:
unda plana
monocromatica progresiva descrie o particula care se
misca in sensul axei x:
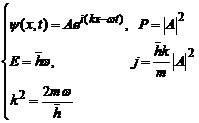
Daca A=0 si B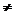 0, avem o unda plana regresiva care se3
misca in sensul negativ al axei ox:
0, avem o unda plana regresiva care se3
misca in sensul negativ al axei ox:
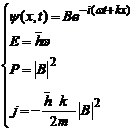
Din 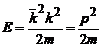 obtinem
obtinem 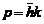 si de aici:
si de aici: 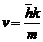 este viteza
clasica a particulei. Acesta difera de viteza de faza a undei,
deformata de :
este viteza
clasica a particulei. Acesta difera de viteza de faza a undei,
deformata de :
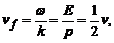
si este
egala cu viteza de grupa undei, deformata de :
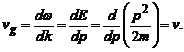
Observam ca, pentru
particulele cu energie (si deci impuls) bine deformata nu stim
nimic despre localizare: densitatea de probabilitate de localizare 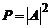 sau
sau 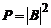 este aceeasi pe
toata axa, nefavorizand nici o pozitie. Aceasta este in acord cu
principiul de incertitudine (cunoasterea precisa a impulsului
este aceeasi pe
toata axa, nefavorizand nici o pozitie. Aceasta este in acord cu
principiul de incertitudine (cunoasterea precisa a impulsului 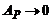 conduce
necunoasterea pozitiei
conduce
necunoasterea pozitiei 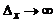 ).
).
2. Pachete de
unde
Undele plane asociate particulelor
libere cu impuls definit sunt complet delocalizate. Pentru a desemna o
particula libera care apartine unei regiuni restranse din
spatiu se poate forma un pachet
de unde, suprapunand unde plane cu diferite numere de unda (impulsul
particulei va fi cuprins acum intr-un
interval, pierzandu-si precizia). Cea mai generala suprapunere de
acest tip este data de integrala:
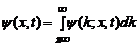
unde 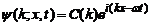 sunt solutii ale
ecuatiei Schrődinger atemporale, unde plane corespund unui numar
de unda k si deci unui impuls
sunt solutii ale
ecuatiei Schrődinger atemporale, unde plane corespund unui numar
de unda k si deci unui impuls 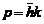 definit. Pentru ca
integrala sa fie convergenta trebuie ca functia amplitudine
definit. Pentru ca
integrala sa fie convergenta trebuie ca functia amplitudine 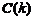 sa tinda la
zona mai repede decat
sa tinda la
zona mai repede decat 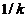 atunci conditia
atunci conditia 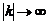 .
.
Vom construi un pachet de unde
care sa desemne o particula
care poseda impulsul 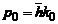 si la
si la 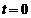 este situata
intr-un mic interval centrat in punctul
este situata
intr-un mic interval centrat in punctul 
Pentru aceasta alegem
:
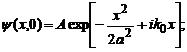
deoarece
densitatea de probabilitate.
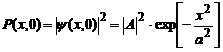
localizeaza
particula in interiorul 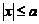 iar densitatea de
curent de probabilitate devine:
iar densitatea de
curent de probabilitate devine:
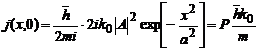
astfel incat
viteza particulei este 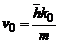 si
si  este impulsul
pachetului de unde. Deoarece functia de unda reprezinta o
particula, conditia de
este impulsul
pachetului de unde. Deoarece functia de unda reprezinta o
particula, conditia de
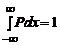
conduce la 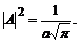
Revenind la formula generala
:
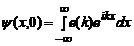
observam
ca aceasta este o integrala Fourier a carei inversa este :
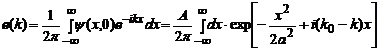
Utilizand formula
: 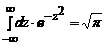 , afla ca:
, afla ca:


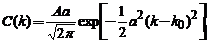
Dupa ce am determinat 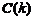 cu ajutorul
starii initiale
cu ajutorul
starii initiale 
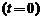 , vom aduna functia de unda la orice moment
, vom aduna functia de unda la orice moment 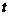 :
:
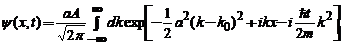
Deoarece exponentul este o form[ p[tratic[ de 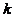 , utilizand iar relatia :
, utilizand iar relatia : 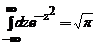 , gasim :
, gasim :
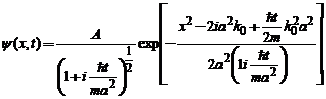
Densitatea de probabilitate de localizare devine :
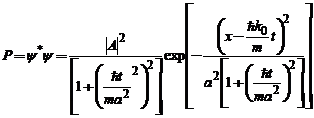
Ea prezinta un maxim care s-a deplasat din 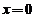 in
in 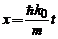 . Spunem sa pachetul de unde se deplaseaza cu
viteza
. Spunem sa pachetul de unde se deplaseaza cu
viteza 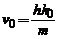 (viteza de grup =
viteza particulei) . Numitorul
exponentului din expresia lui
(viteza de grup =
viteza particulei) . Numitorul
exponentului din expresia lui 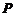 ne arata ca
pachetul de unda s-a largit de la valoarea
ne arata ca
pachetul de unda s-a largit de la valoarea 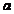 la
la 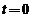 la :
la :
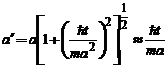 , la momentul
, la momentul 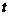 .
.
Densitatea de curent de probabilitate se deduce cu ajutorul
relasiei :
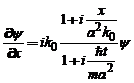 , calculele conducand
la :
, calculele conducand
la :
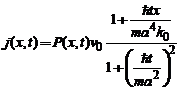 .
.
Rezulta
ca relatia 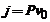 valabila la
valabila la 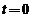 nu se
pastreaza in timp , consecinta a largiri finite a spectrului vitezelor . Daca in centrul pachetului de unde
nu se
pastreaza in timp , consecinta a largiri finite a spectrului vitezelor . Daca in centrul pachetului de unde 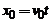 relatia
relatia 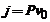 este valabila
, pentru
este valabila
, pentru 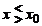 gasim ca
gasim ca 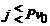 deoarece in aceste
puncte sosesc la momentul
deoarece in aceste
puncte sosesc la momentul 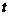 acele parti
ale pachetuli de unde care se misca cu o viteza mai mica
(mare) decat
acele parti
ale pachetuli de unde care se misca cu o viteza mai mica
(mare) decat 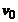 . Se mai poate verifica faptul ca
relatia de normare
. Se mai poate verifica faptul ca
relatia de normare 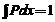 ramane
variabila la orice moment , consecinta a conservarii numarului de particule .
ramane
variabila la orice moment , consecinta a conservarii numarului de particule .
Particula in groapa de potential infinita
Daca pentru o
particula libera energia are spectru continu (adica poate lua
orice valoare pozitiva) , in cazul
particulelor restranse sa se naste doar an anumite regiuni ale spatiului
(particule aflate in stari legate) energia va avea un spectru discret
. O particula dezlegata
sa se mste liber pe axa doar intre punctele 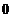 si
si 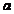 unde se afla pereti inpenetrabili este numita
particula in groapa de potential infinita :
unde se afla pereti inpenetrabili este numita
particula in groapa de potential infinita :
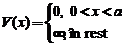
Cautand starile stationare , adica solutiile ecuatiei
Schrödiger atemporiale :
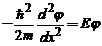
cu conditiile de continuitate 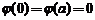 , deoarece
, deoarece 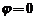 acolo unde
acolo unde 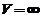 , vom gasi :
, vom gasi :
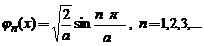
precum si nivelele discrete ale energiei (cuantificate) .
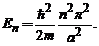
4 Groapa de potential
dreptunghiulara (de adancime finita).
In acest caz 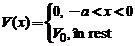
Ecuatia Schrödinger atemporala : 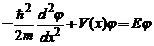 devine :
devine :
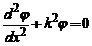 daca
daca 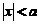 si
si 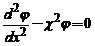 daca
daca 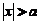 , unde
, unde 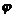 si
si 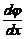 sunt continuie in
sunt continuie in 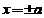 si unde
si unde 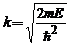 si
si 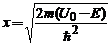 se obtine
solutia :
se obtine
solutia :
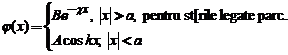
Nivelele energetice ale starilor legate parc se determina
prin rezolvarea numerica sau grfica a ecuatiei transecundante
. Numarul de solutii
creste cu 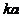 si exista
cel putin o solutie daca
si exista
cel putin o solutie daca 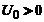 . Energia corespunzatoare este :
. Energia corespunzatoare este : 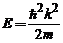 .
.
5. Treapta de potential
Particula se msca pe axa 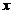 in prezenta
potentialului
in prezenta
potentialului 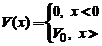
Daca 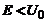 si notam
si notam 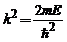 si
si 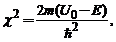 ecuatia de
unda in
ecuatia de
unda in 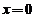 , ne ofera solutia :
, ne ofera solutia :
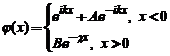 unde
unde 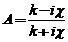 si
si 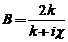
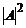 este probabilitatea ca
o particula sa fie reflectata si este egala cu
este probabilitatea ca
o particula sa fie reflectata si este egala cu 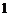 .
.
Daca 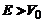 si notam
si notam 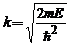 si
si 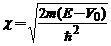 rezolvand
ecuatiile Schrödinger atemporale si impunand continuitatea in
rezolvand
ecuatiile Schrödinger atemporale si impunand continuitatea in 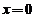 , gasim :
, gasim :
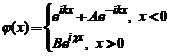 cu
cu 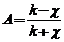 si
si 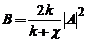 este probabilitatea ca
o particula sa fie reflectata si observam ca ea
se anuleaza doar cand
este probabilitatea ca
o particula sa fie reflectata si observam ca ea
se anuleaza doar cand 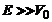 (limita clonica).
(limita clonica).
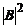 este probabilitatea ca
o particula sa fie gasita tn regiunea
este probabilitatea ca
o particula sa fie gasita tn regiunea 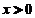 iar
iar  este coeficientul de
transmisie al trapei de potential
este coeficientul de
transmisie al trapei de potential 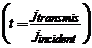 .
.
6. Efectul tunel
Particula se misca pe axa 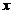 in prezenta
potentialului
in prezenta
potentialului
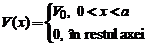
In cazul in care energia este mai mica decat inaltimea
barierei de potential, 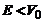 , o particula este intotdeauna reflectata. Vom
arata ca in cazul unei partcule cuantice exista o probabilitate
nenula ca ea sa traverseze bariera chiar daca
, o particula este intotdeauna reflectata. Vom
arata ca in cazul unei partcule cuantice exista o probabilitate
nenula ca ea sa traverseze bariera chiar daca 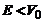 , probabilitate cu atat mai mare cu cat largirea
barierei este mai mica si cu cat diferenta
, probabilitate cu atat mai mare cu cat largirea
barierei este mai mica si cu cat diferenta 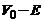 este mai mica.
Acest efect cuantic se numeste efect tunel. Notand
este mai mica.
Acest efect cuantic se numeste efect tunel. Notand 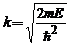 si
si  in ecuatia
Schrödinger atemporala gasim solutia :
in ecuatia
Schrödinger atemporala gasim solutia :
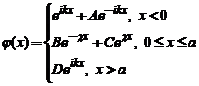
Impunand conditia de continuitate in 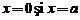 , gasim:
, gasim:
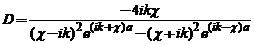 si probabilitatea
de tunelare :
si probabilitatea
de tunelare :
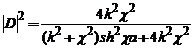
In functie de masa particulei, 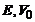 si
si 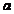 aceasta
probabilitate are valori intr-un domeniu foarte larg. Asfel timpul de
ijumatasire pemrtu dezintegrarea
aceasta
probabilitate are valori intr-un domeniu foarte larg. Asfel timpul de
ijumatasire pemrtu dezintegrarea 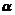 a moleculelor grele
are valori cuprinse intre
a moleculelor grele
are valori cuprinse intre 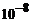 secunde si
secunde si 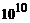 ani.
ani.
7. Oscilatorul liniar armonic
Punctul material de masa 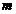 se misca pe
axa
se misca pe
axa 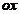 in prezenta unei
forte de tip elastic, avand energia potentiala
in prezenta unei
forte de tip elastic, avand energia potentiala 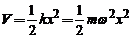 . Ecuatia Schrödinger atemporala :
. Ecuatia Schrödinger atemporala :
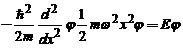 capata o
forma mai simpla daca facem substitutiile :
capata o
forma mai simpla daca facem substitutiile :
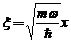 si
si 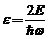 ,
,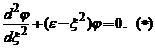
Cand 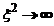 ecuatia
asimtotica devine :
ecuatia
asimtotica devine : 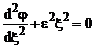 si admite solutiile
si admite solutiile
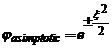 . Retinem solutia
. Retinem solutia 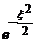 deoarece este
marginita si cautam pentru ecuatia
deoarece este
marginita si cautam pentru ecuatia 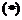 o solutie de
forma :
o solutie de
forma : 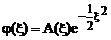 .
.
Introducand in ecuatie obtinem pentru 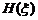 ecuatia
diferentiala:
ecuatia
diferentiala:
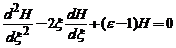 numita ecuatia
Hermite. Punand
numita ecuatia
Hermite. Punand 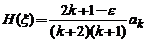 obtinem
relatia de recurenta a coeficientilor :
obtinem
relatia de recurenta a coeficientilor :
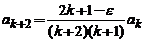
Cerand ca seria de puteri sa devina un polinom pentru ca
functia de unda sa ramana marginita si
notand cu 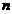 valoarea maxima a
lui
valoarea maxima a
lui 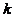 avem :
avem :
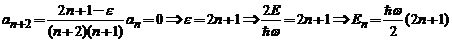 sau
sau
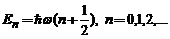
expresie care ne ufera nivelele energetice cuantificate ale
oscilatorului. 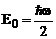 reprezinta
energia de zero a oscilatorului. Functiile
reprezinta
energia de zero a oscilatorului. Functiile 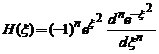 .
.
Avem :
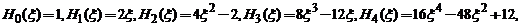
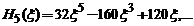
Functiile
proprii ale oscilatorului armonic liniar sunt :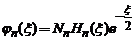 , unde
, unde 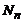 este un factor de
normare.
este un factor de
normare.



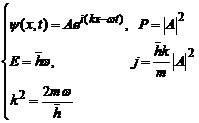
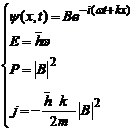
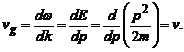
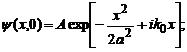
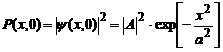
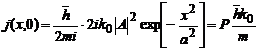
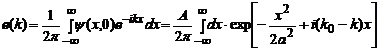
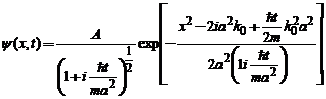
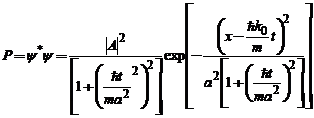
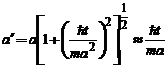 , la momentul
, la momentul 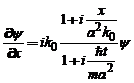 , calculele conducand
la :
, calculele conducand
la :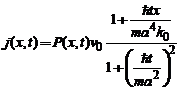 .
.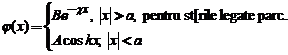
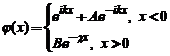 unde
unde 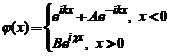 cu
cu 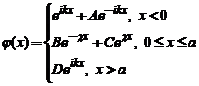
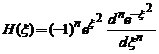 .
.