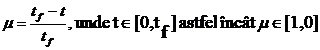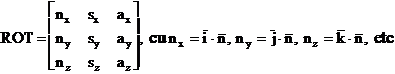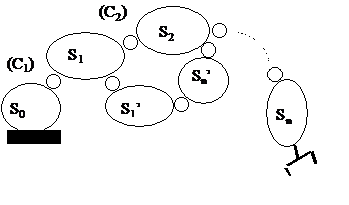FORMULAREA PROBLEMEI PRIVIND GENERAREA MISCARII
NOMINALE A ROBOTILOR DE MANIPULARE
1. Reprezentarea pozitiei
si orientarii efectorului in spatiul de lucru
Fie
spatiul de lucru al unui robot industrial de manipulare, al carui
volum efectiv (V) este definit pe baza restrictiilor geometrice impuse de
mobilitatile limitate din gradele de libertate ale unui mecanism
poliarticulat avand o constructie data.
In
decursul executarii unei activitati de manipulare a obiectelor,
considerate rigide, centrul de prindere (C) din planul efectorului executa
o miscare continua intre punctul de lansare (START) si punctul
de destinatie (FINAL).
Specificul
unei activitati poate sa ceara sau sa permita
eventuale opriri in timpul executiei miscarii, precum si
modificari ale legii de miscare a efectorului, functie de scopul
si obiectivele planificate in cadrul acelei activitati.
Sintetic centrul de prindere executa
un DRUM a carui imagine geometrica (absolut continua) are ca
suport formal o ecuatie diferentiala ordinara.
Figura 1
Miscarea
pe drumul planificat este obligatoriu parametrizata in raport cu un singur
parametru natural, timpul. Conform figurii 1 ca reprezentare analitica se
va folosi vectorul de pozitie 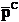 , iar ca parametru normalizat m(t):
definit pe orizontul de timp al activitatii [0, tf] dupa
cum urmeaza
, iar ca parametru normalizat m(t):
definit pe orizontul de timp al activitatii [0, tf] dupa
cum urmeaza
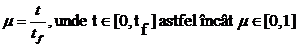 sau
sau
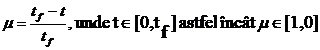
Din
analiza specificatiilor pentru sarcinile de miscare ale robotului
rezulta gradul de netezime al drumului
continuitate in spatiul C0
(legea de miscare discontinua in viteze si acceleratii)
continuitate in spatiul C1
(legea de miscare discontinua numai in acceleratii)
continuitate in spatiul C2
(legea de miscare discontinua in variatia acceleratiei)
Drumul
descris de centrul de prindere este exprimat prin 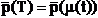 . Manevrarea obiectelor rigide tridimensionale cere insa
si specificarea orientarii efectorului de-a lungul drumului dorit.
. Manevrarea obiectelor rigide tridimensionale cere insa
si specificarea orientarii efectorului de-a lungul drumului dorit.
Spatiul
de efectuare a operatiilor de manipulare, denumit pe scurt spatiul
operational, este inzestrat cu o metrica euclidiana in raport cu
un reper de referinta OXYZ si un sistem ortonormat 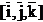 .
.
Daca
vom considera definirea functionala a sistemului ortonormat asociat
efectorului in centrul sau de referinta si anume 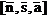 conform figurii nr 1,
unde
conform figurii nr 1,
unde
 este versorul
directiei de apropiere de obiectul care urmeaza a fi apucat
(corespunde axei X a triedrului mobil)
este versorul
directiei de apropiere de obiectul care urmeaza a fi apucat
(corespunde axei X a triedrului mobil)
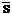 este versorul asociat directiei
de strangere a obiectului (corespunzatoare axei Y)
este versorul asociat directiei
de strangere a obiectului (corespunzatoare axei Y)
 este versorul
directiei normale pe planul de strangere (corespunzatoare axei Z)
este versorul
directiei normale pe planul de strangere (corespunzatoare axei Z)
atunci reprezentarea neomogena a pozitiei
si orientarii efectorului in miscarea pe drumul parametrizat in
timp va fi exprimata formal prin dubletul denumit generic POZITIE
ORIENTARE (POZOR),
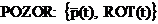 unde
unde 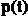 este vectorul de
pozitie al centrului de prindere si ROT este matricea de rotatie
a sistemului
este vectorul de
pozitie al centrului de prindere si ROT este matricea de rotatie
a sistemului 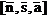 in raport cu sistemul
OXYZ.
in raport cu sistemul
OXYZ.
Cea mai
cunoscuta forma de reprezentare a orientarii reperului 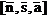 este, conform
modelului din mecanica analitica, matricea cosinusurilor directoare
fata de OXYZ
este, conform
modelului din mecanica analitica, matricea cosinusurilor directoare
fata de OXYZ
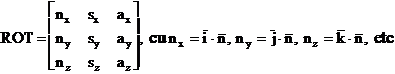
Operatorul
ROT are ca avantaj transparenta necesara explicatarii sarcinilor
de miscare de orientare a efectorului, dar implica, ca dezavantaj
includerea unui nivel inalt de redundanta in calcule (3 unghiuri in
raport cu 9 marimi).
Reprezentarea
neredundanta a pozitiei si orientarii in spatiul
operational are numai valoare simbolica, deoarece vectorul 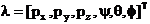 nu intruneste
calitatea de transparenta in ceea ce priveste reprezentarea
orientarii prin trei unghiuri Euler sau trei unghiuri de navigatie.
nu intruneste
calitatea de transparenta in ceea ce priveste reprezentarea
orientarii prin trei unghiuri Euler sau trei unghiuri de navigatie.
In
deceniul trecut, in raport cu nivelul tehnologiilor de fabricatie a
microcalculatoarelor, compatibile IBM-PC, s-a propus realizarea unui compromis
optim intre gradul de redundanta al reprezentarii bazate pe
dubletul 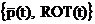 si volumul de
calcul cerut de planificarea miscarii robotilor.
si volumul de
calcul cerut de planificarea miscarii robotilor.
POZOR-ul
a fost exprimat printr-un nou dublet care conserva reprezentarea pozitiei
cu ajutorul vectorului de pozitie 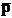 , dar care introducea ca operator de orientare
"quaternionul", definit pe baza teoremei roatiei generalizate in jurul
unei drepte (s) de unghi (d)
, dar care introducea ca operator de orientare
"quaternionul", definit pe baza teoremei roatiei generalizate in jurul
unei drepte (s) de unghi (d) 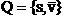 .
.
In
robotica din considerente de normalizare a vectorilor de orientare se
folosesc quaternioni unitari (de norma unitara) astfel incat
rezulta 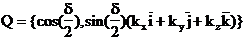 .
.
Definitia
1 Drumul efectorului unui robot manipulator este imaginea
in spatiul operatiilor a dubletului POZOR, explicitat fie sub forma 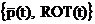 , fie sub forma
, fie sub forma 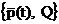 pe tot parcursul
miscarii din START in FINAL, in tot orizontul de timp cat
dureaza miscarea ceruta de activitatea de manipulare, timpul
fiind parametrul unic al ecuatiei de pozitionare si orienate a
efectorului.
pe tot parcursul
miscarii din START in FINAL, in tot orizontul de timp cat
dureaza miscarea ceruta de activitatea de manipulare, timpul
fiind parametrul unic al ecuatiei de pozitionare si orienate a
efectorului.
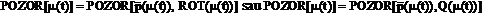 Robotii
industriali au, in general, mecanisme poliarticulate care folosesc cuple de
clasa a V-a cu un singur grad de mobilitate (controlate de servomotoare
rotative sau liniare electrice, electrohidraulice, electropneumatice).
Robotii
industriali au, in general, mecanisme poliarticulate care folosesc cuple de
clasa a V-a cu un singur grad de mobilitate (controlate de servomotoare
rotative sau liniare electrice, electrohidraulice, electropneumatice).
Solutiile
cinematice constructive din aparent foarte variate, se pot clasifica structural
in patru categorii pentru configuratiile complete, prevazute cu sase
grade de libertate.
Reamintim
ca notiunea de grad de libertate pentru un robot semnifica orice
dimensiune independenta (controlata de un servomotor) a
spatiului articular, al coordonatelor generalizate 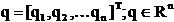 .
.
Daca
se noteaza cu T articulatia de translatie (motor liniar) si
prin R articulatia de rotatie (motor unghiular), solutiile
structurale pot fi exprimate generic pentru robotii cu 6 grade de
libertate (in configuratie completa), dupa cum
urmeaza :
roboti cartezieni
TTT/RRR ;
roboti cilindricii
TTR/RRR ;
roboti sferici
TRR/RRR ;
roboti toroidali RRR/RRR
Figura 2
Lantul cinematic principal al robotului
In toate
cazurile subsistemul de orientare este format numai din articulatii de
rotatie.
Analiza
mecanismului de manipulare al oricarui robot permite identificarea unui
singur lant principal care de regula este un lant deschis.
Lantul se inchide doar in aplicatii cu activitati care
presupun contact mecanic (polizare, montaj, etc).
Datorita
rigiditatii relativ reduse a lantului cinematic care manipuleaza
sarcini importante si care are lungimi baza-virf (efector)
semnificative, robotii industriali includ deseori sublanturi inchise
pentru subsistemele de pozitionare (figura nr 2).
Pentru
analiza cinematica, apelata in generarea automata a
miscarii robotilor, este suficient sa consideram
ansamblul de trei ipoteze simplificatoare care usureaza modelarea
acestora
T1
(fundamentala) Mecanismul de pozitionare si orientare
al efecorului unui robot industrial este reprezentat de un lant deschis.
NOTA :
Pentru configuratii complete 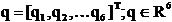 avem:
avem:
Daca
robotul are structura de mecanism incomplet 4 n<6
(caz particular robot planar n3 RR-/-R-) iar daca solutia are n>6
atunci se spune ca sistemul de pozitionare/orientare al robotului
este redundant.
T2
Segmentele lantului cinamatic sunt considerate perfect rigide, astfel
incat "sageata" la nivelul organului terminal, efectorul, este zero
indiferent de valoarea sarcinii.
T3
Lantul cinematic are cuple ideale Cj, j=1,2, n-1, fara frecare si jocuri
mecanice.
NOTA In
realitate comportarea unei cuple reale introduce neliniaritati
puternice in modelarea miscarii robotilor, de tip histeresis
mecanic datorat fortelor in angrenajul reductoarelor reale ale
mecanismului (figura 3).
Figura 3
unde qmi
este axul motor, qi este axul articulatiei, Ff este
forta generalizata de frecare si 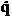 este viteza
articulatiei.
este viteza
articulatiei.
Drumul
efectorului "vizualizat" in spatiul operational este rezultatul
miscarii simultane a tuturor sau numai unora dintre axele
servomotoarelor robotului.
Definitia
2 Traiectoria unui robot manipulator este imagine din
spatiul coordonatelor generalizate (netransparent pentru inginerul de
aplicatie, dar singurul spatiu controlabil prin activarea
servomotoarelor robotului) pe tot parcursul miscarii din START in
FINAL in tot orizontul de timp [0.tf] repartizat activitatii
date.
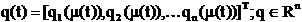 .
.
Din
compararea definitiei 1 (pentru drum) si a definitiei 2 (pentru
traiectorie) rezulta obligativitatea stabilirii unei corespondente
biunivoce intre cele doua reprezentari in spatiul
operatiilor si respectiv, in spatiul coordonatelor
generalizate , conform figurii nr 4.
Figura 4