ROTI DINTATE
Rotile dintate fac parte din categoria organelor de masini care se folosesc
la transmiterea miscarii de rotatie intre doua axe , fara a se deprecia raportul
de transmisie al acestora . Rotile dintate transmit miscarea de la una la alta
prin intermediul unor proeminente , cara sunt permanent in contact , prelund de
la una la alta momentul de rotatie , respectiv forta tangentiala
, asigurand astfel
functionarea acelei imbinari mobile , imbinare care se chiama angrenaj
, iar
proieminentele se numesc dintii angrenajului.
Rotile dintate se clasifica dupa doua criterii :
a)
Dupa forma suprafetei de rostogolire a organului generator :
- roti dintate cilindrice ;
- roti dintate conice ;
- roti dintate hiperboloide ;
- roti dintate melcate si melc cilindric conjugat .
b) Dupa forma si directia dintilor pe latimea coroanei dintate :
- roti dintate cu dinti drepti ;
- roti dintate cu dinti inclinati ;
- roti dintate in V ;
- roti dintate cu dinti curbi .
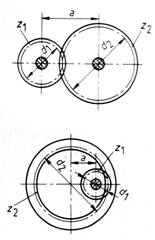
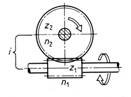
Angrenajele dintate prin constuctie asigura un raport de transmisie a
miscarii , care este dat de raportul numarului de dinti a celor doua roti
conjugate ale angrenajului ( fig. 45 ) :
z n
i = --- , sau inversul raportul turatiilor celor doua axe :--- .
z n
1.
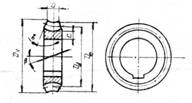
ROTI DINTATE CILINDRICE ( STAS 5013 - 82 )
Elemente cinematice si geometrice
p d
m - modulul = -- = -- ;
π z
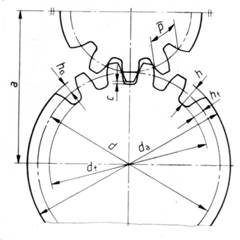
p - pasul la dinte = π . m ;
d da - 2.m
z - numar dinti = -- = ---- ;
m m
d - diametru de divizare = m . z
=
z . p
-- ;
 π
π
da - diametrul de varf ( exterior )
= d + 2 . m ;
= m . ( z + 2 ) .
d f - diametrul de fund (interior )
= d - 2 . ( m + c ) .
c - jocul la fund = 0,1 . m pana la
0,3 . m .
h - inaltimea dintelui = 2. m + c . Fig. 45
h f - inaltimea piciorului dintelui = m + c . ha - inaltimea varf dinte = m
.
d d m . ( z + z )
a - distanta dintre axele rotilor angrenajului = --- = ------ ,
2 2
pentru angrenare exterioarǎ sau a
= ( d2 - d )
/ 2 , pentru angrenare interioarǎ .
EXEMPLU : Sa se calculeze elementele unui angrenaj cilindric la care se
cunosc :z = 20
, i = 2 si m = 1,5 .
REZOLVARE
:
z 2 z
- i = -- = -- = 2,0
→ z2 = 2,0 . 20 = 40 .
z 20
- d = m
. z
1 = 1,5 . 20 = 30 mm ;
- d = m
. z
2 = 1,5 . 40 = 60 mm ;
- d a = d + 2 . m
= 30 + 2 . 1,5 = 30 + 3 = 33 mm ;
- d a = d + 2 . m
= 60 + 2 . 1,5 = 60 + 3 = 63 mm ;
- d f1= d - 2 . ( m + c ) = 30 - 2 . ( 1,5 + 0,3 . 1,5 ) = 30-3,9= 26,1 mm ;
- d f2= d - 2 . ( m + c ) = 60 - 2 . ( 1,5
+ 0,3 . 1,5 ) = 60-3,9= 56,1 mm;
- h = 2 . m + c = 2 . 1,5 + 0,45 = 3,45 mm ;
- h
f = m + c = 1,5 + 0,45 = 1,95 mm ;
- h
a = m = 1,5 mm ;
d + d 2 30 + 60
- a = ---- = ---- = 45 mm .
2 2
2. ROTI DINTATE MELCATE SI MELC CONJUGAT(STAS 6649 - 74 )
2.1. MELCUL CONJUGAT
Elemente cinematice si geometrice
Pentru roata dintata melcata elementele cinematice si geometrice sunt , in mare, ca la rotile dintate cilindrice cu deosebirea ca m se inlocuieste cu ma - modul
axial . Insa pentru melc se considera elementele cinematice si geometrice de mai
jos rezultate din configurarea melcului de referinta .
a) ELEMENTE CARE DETERMINǍ FORMA SI DIMENSIUNILE MELCULUI DE REFERINTǍ
ma - modul axial (valori standardizate mai mari de 1 ) ;
z - numar de dinti ( inceputuri ) 1 ≤ ;
- sens inclinare dantura ( stanga sau dreapta ) ;
Do - diametrul de referinta = q . ma ,
unde q coeficient diametral , cu valori
ce se adopta din tabelul urmator .
ma
|
|
|
|
4,5 . . 6
|
|
|
|
q
|
12
|
10
|
10
|
9
|
9
|
8
|
7
|
|
14
|
12
|
11
|
10
|
10
|
9
|
8
|
16
|
14
|
13
|
12
|
11
|
10
|
9
|
NOTǍ : Valorile ingrosate din tabel sunt recomandabile .
a ; n - unghiul de presiune axial de referinta sau unghiul de presi-
une normal de referinta = 20° .
a 0 inaltimea capului spirei de referinta = f a . ma = 1 . ma ;
( f a - coeficient cremaliera de referinta , care la situatii normale
s-a stabilit o valoare egala cu 1 pentru capul de dinte sau
spira )
c 0 - jocul de referinta la fund = w a . ma = 0,25 . ma ;
( w a - coeficient de fund cremaliera de referinta = 0,25 )
b) ELEMENTE REZULTATE
pa - pasul axial = π . ma ;
pE - pasul elicei = z . π . ma ;
z
0 - unghiul elicei de referinta = arctg -- ;
q
b 0 - inaltimea piciorului de referinta = 1.25 . ma ;
h 0 -
inaltimea dintelui de referinta = 2,25 . ma ;
De - diametrul de varf = ma . (
q + 2 ) ;
Di - diametrul de fund = ma . ( q - 2,5 ) .
p n - pasul normal pe spira = π . ma . cos θ°
mn - modulul normal = ma . cos θ°
.
c) ELEMENTE EXECUTIE MELC
r 0 - raza la fund de racordare flanc = max. 0,3.
m n;
b - latimea deschiderii
la fund ( latimea
cutitului de prelu-
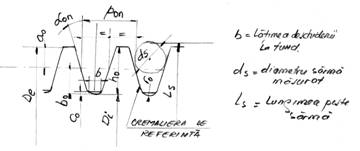 crat ) = p n/2 -
crat ) = p n/2 -
(D0 - Di ) . tg 20°;
ds - diametrul sarmei
de masurat , care
se adopta din trusa
ZEISS , astfel
:
ds ≥ p n / ;
Ls- lungimea peste
sarmele de masu-
rat =D + 3,91.ds
-1,37 . p n
Fig.46
EXEMPLU : Sa se calculeze elementele unui melc , care are ma= 1,5 ,
q = 14
; z = 1 si a = 20 ° .
REZOLVARE :
a 0 = 1 . ma = 1 . 1,5 = 1,5 mm ;c 0 = 0,25 . ma = 0,25 .1,5 = 0,375 mm;
D0 = q . ma = 14 . 1,5 = 21 mm ;
pa = π . ma = 3,14 . 1,5 = 4,71 mm ; pE = z . π . ma =1 . 3,14 . 1,5 = 4,71 mm ; ° = arctgz /q = arctg
1/ 14 = arctg 0,071 = 4 ° (valoare din tabel ) ; b = 1,25 . ma = 1,25 . 1,5 = 1,875 mm ; h = 2,25 . ma = 2,25 .1,5= 3,375 mm;
De = ma . ( q + 2 ) = 1,5 . ( 14 + 2 )
= 1,5 . 16 = 24 mm ;
Di = ma . ( q - 2,5
) = 1,5 . ( 14 - 2,5 ) = 1,5 . 11,5 = 17,25 mm ;
p
n= π . ma . cos θ° = 3,14 . 1,5 . cos 4°
= 3,14 . 1,5 . 0,99 = 4,66 mm ;
mn
= ma . cos = 1,5 . cos 4
° = 1,5 . 0,99 = 1,48 mm ;
r 0 = 0,3 . mn = 0,3 . 1,48 = 0,434 mm ;
b = p n/
2 - ( D0 - Di ) . tg 20° = 2,33 - (
21 - 17,5 ) . 0,364 = 0,97
mm ;
ds = 2,55
mm , valoare adoptata din tabelul 1., astfel : ds ≥ p n/ 2
( 2,33 mm) ;
Ls = D + 3,91 . ds - 1,37 . p n = 21 + 3,91 . 2,55 - 1,37 . 4,66 =24,59 mm.
TABEL 1. DIAMETRUL SARMA TRUSA ZEISS
Valorile din tabel sunt in mm
2.2.
ROATA DINTATA MELCATA
ELEMENTELE ROTII DINTATE MELCATE:
La
fel ca la melc elementele cinematice sunt aceleasi , facand exceptie cele con-
structive , astfel : ma , a 0 , c 0 , pa
, b 0 , h 0 , p n si mn au aceas formula de ex-
primare si determinare , iar cele constructive se determina cu relatiile de mai
jos.
Dd - diametrul de divizare al rotii = ma
. z ;
 De - diametrul exterior al rotii = Dd + 2 . mn
;
De - diametrul exterior al rotii = Dd + 2 . mn
;
Dv - diametrul de varf al rotii = De +
( Dd - 2
. mn
) . ( 1 - cos β°) ;
β° - unghiul de inclinare al dintelui = =
pE
arc
tg --- , unde pE - pasul elicei melc,
D .
si D0 - diametrul de divizare melc . Fig. 47
z - numar dinti roata melcata si rezulta din
relatia : n z
i = -- = -- , unde z2 = i. z
n z
b - latimea dintilor la varful rot ii = 1,5 . 2 . pa ;
sd - grosimea dintelui in plan normal = 0,5 . p n
 B - latimea rotii melcate = b + 0,25 . pa .
B - latimea rotii melcate = b + 0,25 . pa .
Fig.
48
TABEL
2 - VALORILE ELEMENTELOR CONSTUCTIVE
ALE DANTURII ROTILOR DINTATE IN RAPORT DE
MODULUL ADOPTAT
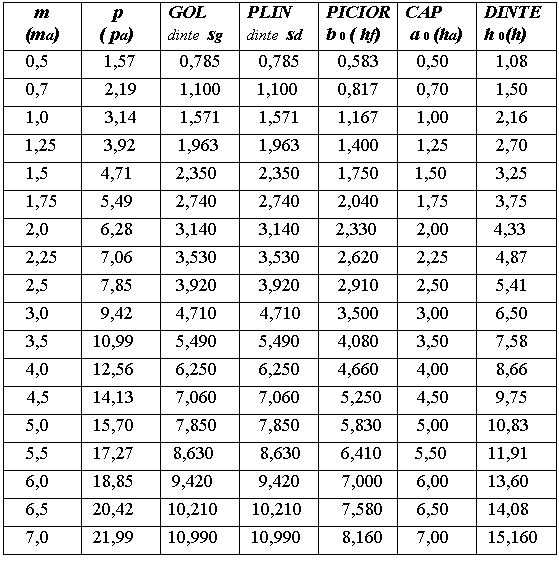 Valorile di tabel sunt in mm
Valorile di tabel sunt in mm
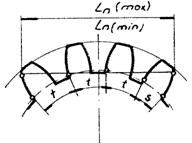
3. MASURAREA ROTILOR DINTATE CILINDRICE
CU DINTI DREPTI
Dantura normala se verifica prin metoda cotei peste dinti ,
care determina
distanta peste un numar determinat de dinti Ln ,
masurat pe cercul de baza al
danturii.
Fig. 49
Expresia care determina cota peste n dinti se prezinta astfel:
Ln = m
. Ln1 , unde m - modulul rotii de masurat ,
iar Ln - lungimea peste un numa de dinti corespunzator numarului dat de dinti
de la roata dintata de masurat , pentrul modulul de 1 ( m = 1 ).Valoarea lui Ln a
fost calculata pentru zmin.= 4 si zmax. = 300 ( n =
20°) , in mm si este prezen-
tata in tabel 3.
TABEL
3. - VALORILE Ln1 si n -NUMARUL DE DINTI PESTE CARE
SE
EFECTUEAZA MASURATOAREA
(m=1 ; z = 4 300 ; α°0n = 20° ) Valorile din tabel sunt in mm
|
α°
|
20°
|
α°
|
20°
|
α°
|
20°
|
α°
|
20°
|
|
z
|
n
|
Ln
|
z
|
n
|
Ln
|
z
|
n
|
Ln
|
z
|
n
|
Ln
|
|
4
|
|
4,4842
|
79
|
10
|
29,1517
|
154
|
18
|
53,8192
|
229
|
27
|
81,4388
|
|
5
|
2
|
4,4982
|
80
|
10
|
29,1657
|
155
|
18
|
53,8332
|
230
|
27
|
81,4528
|
|
6
|
2
|
4,5122
|
81
|
10
|
29,1797
|
156
|
19
|
56,7993
|
231
|
27
|
81,4668
|
|
7
|
2
|
4,5263
|
82
|
10
|
29,1937
|
157
|
19
|
56,8133
|
232
|
27
|
81,4808
|
|
8
|
2
|
4,5403
|
83
|
10
|
29,2077
|
158
|
19
|
56,8273
|
233
|
27
|
81,4948
|
|
9
|
2
|
4,5543
|
84
|
10
|
29,2217
|
159
|
19
|
56,8413
|
234
|
27
|
81,5088
|
|
10
|
2
|
4,5683
|
85
|
10
|
29,2357
|
160
|
19
|
56,8553
|
235
|
28
|
84,4749
|
|
11
|
2
|
4,5823
|
86
|
10
|
29,2497
|
161
|
19
|
56,8693
|
236
|
28
|
84,4889
|
|
2
|
4,5963
|
87
|
11
|
32,2159
|
162
|
19
|
56,8833
|
237
|
28
|
84,5029
|
|
13
|
2
|
4,6103
|
88
|
11
|
32,2299
|
163
|
19
|
56,8973
|
238
|
28
|
84,5169
|
|
14
|
2
|
4,6243
|
89
|
11
|
32,2439
|
164
|
19
|
56,9113
|
239
|
28
|
84,5309
|
|
15
|
2
|
4,6383
|
90
|
11
|
32,2519
|
165
|
20
|
59,8775
|
240
|
28
|
84,5449
|
|
16
|
2
|
4,6523
|
91
|
11
|
32,2719
|
166
|
20
|
59,8915
|
241
|
28
|
84,5589
|
|
17
|
3
|
7,6184
|
92
|
11
|
32,2859
|
167
|
20
|
59,9055
|
242
|
28
|
84,5730
|
|
18
|
3
|
7,6324
|
93
|
11
|
32,2999
|
168
|
20
|
59,9195
|
243
|
29
|
87,5391
|
|
19
|
3
|
7,6464
|
94
|
11
|
32,3139
|
169
|
20
|
59,9335
|
244
|
29
|
87,5531
|
|
20
|
3
|
7,6605
|
95
|
11
|
32,3279
|
170
|
20
|
59,9475
|
245
|
29
|
87,5671
|
|
21
|
3
|
7,6145
|
96
|
12
|
35,2940
|
171
|
20
|
59,9615
|
246
|
29
|
87,5811
|
|
22
|
3
|
7,6885
|
97
|
12
|
35,3080
|
172
|
20
|
59,9755
|
247
|
29
|
87,5951
|
|
23
|
3
|
7,7025
|
98
|
12
|
35,3220
|
173
|
20
|
59,9895
|
248
|
29
|
87,6091
|
|
24
|
3
|
7,7165
|
99
|
12
|
35,3361
|
174
|
21
|
62,9557
|
249
|
29
|
87,6231
|
|
25
|
3
|
7,7305
|
100
|
12
|
35,3501
|
175
|
21
|
62,9697
|
250
|
29
|
87,6371
|
|
26
|
4
|
10,6966
|
101
|
12
|
35,3641
|
176
|
21
|
62,9837
|
251
|
30
|
90,6033
|
|
27
|
4
|
10,7106
|
102
|
12
|
35,3781
|
177
|
21
|
62,9977
|
252
|
30
|
90,6173
|
|
28
|
4
|
10,7246
|
103
|
12
|
35,3921
|
178
|
21
|
63,0117
|
253
|
30
|
90,6313
|
|
29
|
4
|
10,7386
|
104
|
13
|
38,3582
|
179
|
21
|
63,0257
|
254
|
30
|
90,6453
|
|
30
|
4
|
10,7526
|
105
|
13
|
38,3722
|
180
|
21
|
63,0397
|
255
|
30
|
90,6593
|
|
31
|
4
|
10,7666
|
106
|
13
|
38,3862
|
181
|
21
|
63,0537
|
256
|
30
|
90,6733
|
|
32
|
4
|
10,7806
|
107
|
13
|
38,4002
|
182
|
21
|
63,0677
|
257
|
30
|
90,6873
|
|
33
|
4
|
10,7946
|
108
|
13
|
38,4143
|
183
|
22
|
66,0338
|
258
|
30
|
90,7013
|
|
34
|
4
|
10,8086
|
109
|
13
|
38,4283
|
184
|
22
|
66,0479
|
259
|
30
|
90,7153
|
|
35
|
5
|
13,7748
|
110
|
13
|
38,4423
|
185
|
22
|
66,0619
|
260
|
31
|
93,6814
|
|
36
|
5
|
13,7888
|
111
|
13
|
38,4563
|
186
|
22
|
66,0759
|
261
|
31
|
93,6955
|
|
37
|
5
|
13,8028
|
112
|
13
|
38,4703
|
187
|
22
|
66,0899
|
262
|
31
|
93,7095
|
|
38
|
5
|
13,8168
|
113
|
14
|
41,4364
|
188
|
22
|
66,1039
|
263
|
31
|
93,7235
|
|
39
|
5
|
13,8308
|
114
|
14
|
41,4504
|
189
|
22
|
66,1179
|
264
|
31
|
93,7375
|
|
40
|
5
|
13,8448
|
115
|
14
|
41,4644
|
190
|
22
|
66,1319
|
265
|
31
|
93,7515
|
|
41
|
5
|
13;8588
|
116
|
14
|
41,4784
|
191
|
23
|
69,0980
|
266
|
31
|
93,7655
|
|
42
|
5
|
13,8728
|
117
|
14
|
41,4924
|
192
|
23
|
69,1120
|
267
|
31
|
93,7795
|
|
43
|
5
|
13,8868
|
118
|
14
|
41,5064
|
193
|
23
|
69,1260
|
268
|
31
|
93,7935
|
|
44
|
6
|
16,8530
|
119
|
14
|
41,5204
|
194
|
23
|
69,1400
|
269
|
32
|
95,7596
|
|
45
|
6
|
16,8669
|
120
|
14
|
41,5344
|
195
|
23
|
69,1540
|
270
|
32
|
96,7736
|
|
46
|
6
|
16,8810
|
121
|
14
|
41,5485
|
196
|
23
|
69,1680
|
271
|
32
|
96,7876
|
|
47
|
6
|
16,8950
|
122
|
15
|
44,5146
|
197
|
23
|
69,1820
|
272
|
32
|
96,8016
|
|
48
|
6
|
16,9090
|
123
|
15
|
44,5286
|
198
|
23
|
69,1961
|
273
|
32
|
96,8157
|
|
49
|
6
|
16,9230
|
124
|
15
|
44,5426
|
199
|
24
|
72,1622
|
274
|
32
|
96,8297
|
|
50
|
6
|
16,9370
|
125
|
15
|
44,5566
|
200
|
24
|
72,1762
|
275
|
32
|
96,8437
|
|
51
|
6
|
16,9510
|
126
|
15
|
44,5706
|
201
|
24
|
72,1902
|
276
|
32
|
96,8577
|
|
52
|
7
|
19,9171
|
127
|
15
|
44,5846
|
202
|
24
|
72,2042
|
277
|
32
|
96,8717
|
|
53
|
7
|
19,9311
|
128
|
15
|
44,5986
|
203
|
24
|
72,2182
|
278
|
33
|
99,8378
|
|
54
|
7
|
19,9451
|
129
|
15
|
44,6162
|
204
|
24
|
72,2322
|
279
|
33
|
99,8518
|
|
55
|
7
|
19,9592
|
130
|
16
|
47,5788
|
205
|
24
|
72,2462
|
280
|
33
|
99,8658
|
|
56
|
7
|
19,9732
|
131
|
16
|
47,5928
|
206
|
24
|
72,2602
|
281
|
33
|
99,8798
|
|
57
|
7
|
19,9872
|
132
|
16
|
47,6078
|
207
|
24
|
72,2742
|
282
|
33
|
99,8938
|
|
58
|
7
|
20,0012
|
133
|
16
|
47,6208
|
208
|
25
|
75,2404
|
283
|
33
|
99,9078
|
|
59
|
7
|
20,0152
|
134
|
16
|
47,6348
|
209
|
25
|
75,2544
|
284
|
33
|
99,9218
|
|
60
|
7
|
20,0292
|
135
|
16
|
47,6488
|
210
|
25
|
75,2684
|
285
|
33
|
99,9358
|
|
61
|
8
|
22,9953
|
136
|
16
|
47,6628
|
211
|
25
|
75,2824
|
286
|
34
|
102,9020
|
|
62
|
8
|
23,0093
|
137
|
16
|
47,6768
|
212
|
25
|
75,2964
|
287
|
34
|
102,9160
|
|
63
|
8
|
23,0233
|
138
|
16
|
47,6908
|
213
|
25
|
75,3104
|
288
|
34
|
102,9300
|
|
64
|
8
|
23,0373
|
139
|
17
|
50,6569
|
214
|
25
|
75,3244
|
289
|
34
|
102,9440
|
|
65
|
8
|
23,0513
|
140
|
17
|
50,6709
|
215
|
25
|
75,3384
|
290
|
34
|
102,9580
|
|
66
|
8
|
23,0654
|
141
|
17
|
50,6849
|
216
|
25
|
75,3524
|
291
|
34
|
102,9720
|
|
67
|
8
|
23,0794
|
142
|
17
|
50,6989
|
217
|
26
|
78,3186
|
292
|
34
|
102,9860
|
|
68
|
8
|
23,0934
|
143
|
17
|
50,7129
|
218
|
26
|
78,3326
|
293
|
34
|
103,0000
|
|
69
|
8
|
23,1074
|
144
|
17
|
50,7270
|
219
|
26
|
78,3466
|
294
|
34
|
103,0140
|
|
70
|
9
|
26,0735
|
145
|
17
|
50,7410
|
220
|
26
|
78,3606
|
295
|
35
|
105,9802
|
|
71
|
9
|
26,0875
|
146
|
17
|
50,7550
|
221
|
26
|
78,3746
|
296
|
35
|
105,9942
|
|
72
|
9
|
26,1015
|
147
|
17
|
50,7690
|
222
|
26
|
78,3886
|
297
|
35
|
106,0082
|
|
73
|
9
|
26,1155
|
148
|
18
|
53,7351
|
223
|
26
|
78,4026
|
298
|
35
|
106,0222
|
|
74
|
9
|
26,1295
|
149
|
18
|
53,7491
|
224
|
26
|
78,4166
|
299
|
35
|
106,0362
|
|
75
|
9
|
26,1435
|
150
|
18
|
53,7631
|
225
|
26
|
78,4306
|
300
|
35
|
106,0502
|
|
76
|
9
|
26,1575
|
151
|
18
|
53,7771
|
226
|
27
|
81,3967
|
|
|
|
|
77
|
9
|
26,1715
|
152
|
18
|
53,7911
|
227
|
27
|
81,4107
|
|
|
|
|
78
|
10
|
29,1377
|
153
|
18
|
53,8051
|
228
|
27
|
81,4247
|
|
|
|
CALCULUL COTEI PESTE DINTI CAND SE CUNOSC NUMARUL DE DINTI SI MODULUL ROTII DIN ANGRENAJ ( z ,m )
Aplicad formola :Ln = Ln1 . m si tabelul 3.
EXEMPLU
: Se da z / z =73/
73 ; modulul m
4,5 si n =
20° :
Se cere n( numarul de dinti peste care se efectueaza
masuratoarea) si Ln (
cota peste dinti ,in mm) .
REZOLVARE :
Din tabelul 3. ,pentru z= 73 , n = 9 si Ln = 26,1155 mm :
Formula de mai sus devine : L = 4,5 . 26,1155 = 117,519 mm,
L9 = 117,519 mm.
OBSERVATIE:
Aceasta metoda de masurare se aplica si la rotile dintate cilindrice cu dinti
inclinati , unde formula de determinare este mai complexa , implicand o serie de co-
eficienti , pe care literatura de specialitate ii prezinta ( INDRUMATOR practic
si
de perfectionare
,Editia 1982 , autor N.MITRICEL ,pagina 202 ).