Calculul principalilor indicatori dinamici ai eficientei
economice a investitiilor
Pentru a
determina indicatorii de eficienta economica a
investitiilor in viziune dinamica, in oricare dintre momentele de
referinta prezentate, este necesara parcurgerea
urmatoarelor etape:
stabilirea indicatorului ce urmeaza a fi actualizat
si determinarea formei sale statice, pentru ca aceasta sa fie
comparata cu marimea dinamica;
stabilirea momentului de referinta, la care se
doreste realizarea calculului de actualizare;
trasarea triunghiurilor actualizarii - reprezentarea
investitiilor si a profiturilor, stabilind astfel formula de calcul,
respectiv, utilizand factorul de actualizare sau cel de fructificare;
calculul valorii actualizate a indicatorului si
interpretarea rezultatelor.
Metodologia prezentata se va aplica in calculul indicatorilor de
eficienta actualizati, in fiecare moment de referinta
prezentat.
A. Actualizarea la momentul luarii deciziei de
investitii
In acest
caz, triunghiurile actualizarii sunt prezentate in figura 3.8.
m0 m0' m1 m2 timp

g d De
I
P
Fig. 3.8. Schema de calcul
Se calculeaza, pentru inceput, valorile
investitiei si profiturilor actualizate la m0:
 (3.44;
3.45)
(3.44;
3.45)
Daca profiturile anuale sunt constante pe
toata durata de functionare a obiectivului, atunci:
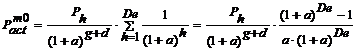 (3.46)
(3.46)
Pe
baza acestor relatii se pot calcula indicatorii de
eficienta economica a investitiilor actualizati.
Prezinta interes: randamentul economic
si termenul de recuperare a investitiei in viziune dinamica.
1.
Randamentul economic actualizat:
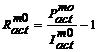 . (3.47)
. (3.47)
2.
Termenul de recuperare a investitiei, actualizat:
Termenul de recuperare a investitiei, in
viziune dinamica, se calculeaza construind o ecuatie in
aceasta necunoscuta, pornind de la definitia indicatorului,
adica perioada de timp dupa
care sumele investite se recupereaza din profiturile cumulate. Calculul se
poate efectua mai simplu considerand
profitul anual constant.
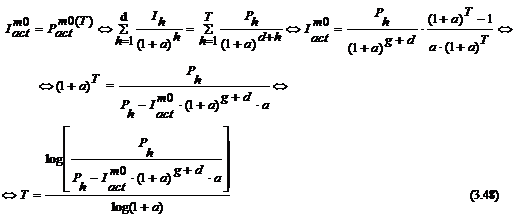
Relatia
de calcul se poate simplifica in cazul in care profiturile anuale sunt
diferite, considerandu-le egale cu profitul mediu anual Ph, calculat ca medie aritmetica a profiturilor
anuale.
Exemplu: in cazul
aplicatiei de realizare a unui sistem tehnico-economic cu specific de
productie ce va realiza subansambluri auto, pentru care s-au prezentat
indicatorii de eficienta economica a investitiei in tabelul
3.3, dar in forma statica, se calculeaza randamentul economic
si termenul de recuperare actualizati, la momentul luarii
deciziei de investitii. Se considera o rata de actualizare a = 15% si o perioada
afectata proiectarii de 1 an se adauga perioadei de realizare a
obiectivului. Calculele se realizeaza doar pentru varianta V1 de proiect.
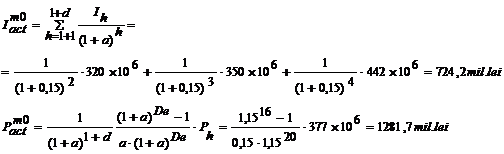
Pe baza acestor valori se calculeaza
randamentul economic actualizat, la momentul luarii decizei:
 lei profit actualizat, la 1 leu investit.
lei profit actualizat, la 1 leu investit.
Daca randamentul economic al
investitiei, calculat static, era de 4,42 lei, cel dinamic are valoarea de
0,77, deci de aproape 6 ori mai mic.
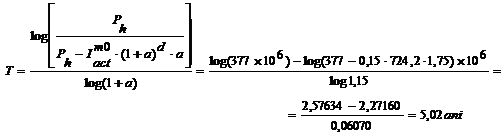
Se constata ca si acest indicator este mai
putin favorabil decat cel static, care a fost de 2,94 ani.
In cazul in care, de interes pentru calculul eficientei
economice a investitiilor, este momentul inceperii lucrarilor de
investitii, procedura de lucru si formulele pentru determinarea
indicatorilor actualizati, sunt identice celor anterior prezentate. In
acest caz se neglijeaza perioada g, de
cercetare-proiectare, in care se elaboreaza documentatia
tehnico-economica pentru noul obiectiv. Succint, elementele de calcul sunt
prezentate in continuare:
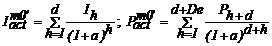 , (3.49;
3.50)
, (3.49;
3.50)
dar
atunci cand profiturile anuale sunt constante:
 . (3.51)
. (3.51)
Deci, randamentul actualizat in momentul inceperii
lucrarilor de investitii este:
 , (3.52)
, (3.52)
iar
termenul de recuperare actualizat la acelasi moment se calculeaza in
conformitate cu aceeasi procedura:
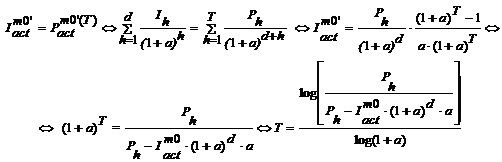
Exemplu: Pentru aceeasi
aplicatie descrisa de datele din tabelul 3.3, calculul indicatorilor
de eficienta economica, in viziune dinamica, sunt:
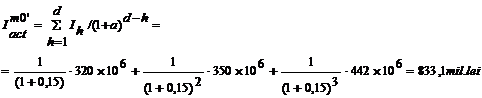
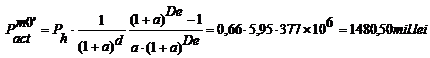
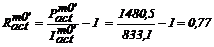 lei profit final, la
1 leu investit.
lei profit final, la
1 leu investit.

B.
Actualizarea la momentul punerii in functiune a noului obiectiv
Triunghiurile actualizarii, in acest caz,
sunt prezentate in figura 3.9.
 m0 m1 m2 timp
m0 m1 m2 timp
d De
I
P
Fig. 3.9.
Schema de calcul
Investitiile
si profitul actualizate la momentul m1
sunt calculate astfel:
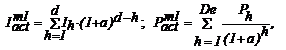 (3.54; 3.55)
(3.54; 3.55)
iar cand profiturile anuale sunt constante,
rezulta:
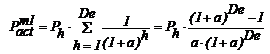 (3.56)
(3.56)
1. Randamentul economic actualizat:
 (3.57)
(3.57)
2. Termenul de recuperare al investitiei,
actualizat:
Aplicand acelasi
artificiu de calcul, se obtine:
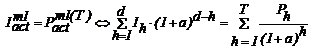 .
.
Cand profiturile anuale
sunt constante, atunci:
 (3.58)
(3.58)
Exemplu Pentru aceeasi situatie investitionala descrisa
static in tabelul 3.3, calculul indicatorilor de eficienta in
momentul inceperii lucrarilor de investitii este:
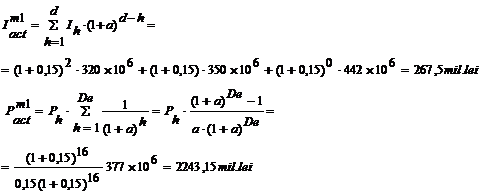
Randamentul si
termenul de recuperare actualizat, in acest caz, sunt:
 lei profit final, la 1leu investita
lei profit final, la 1leu investita
Se precizeaza ca randamentul economic actualizat la momentul
inceperii functionarii obiectivului este egal cu cel calculat pentru
momentul luarii deciziei. De altfel, randamentul economic al
investitiilor actualizat, indiferent de momentul de referinta
ales, va avea aceeasi valoare.
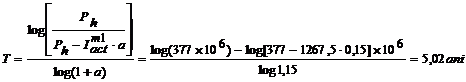
Precizam ca intotdeauna termenul de recuperare actualizat este
mai mic decat cel static, ceea ce arata ca influenta factorului
timp se face in sensul diminuarii eficientei economice.
C.
Actualizarea la momentul inceperii restituirii creditelor primite
Triunghiurile actualizarii in acest caz sunt prezentate in figura 3.10.
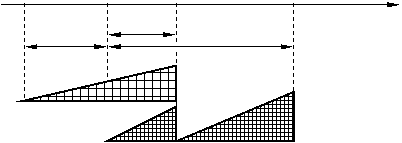 m0 m1 m1' m2 timp
m0 m1 m1' m2 timp
f
d De
I
P1 P2
Fig.3.10. Schema de
calcul
Investitia si
profiturile actualizate, in momentul m1',
sunt date de relatiile:
 (3.59; 3.60)
(3.59; 3.60)
Cand
profiturile anuale sunt constante:
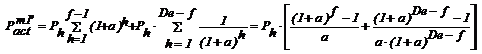
1. Randamentul economic actualizat:
 (3.61)
(3.61)
2. Termenul de recuperare al investitiei,
actualizat:
Calculul termenului de
recuperare actualizat la momentul inceperii restituirii creditelor primite, se
pot intalni doua situatii:
cazul in care
termenul de recuperare actualizat este mai mic decat perioada cuprinsa
intre momentul inceperii functionarii noului obiectiv si
momentul inceperii restituirii creditelor: T
< f
cazul invers: T > f
Aplicand acelasi
artificiu de calcul, se obtine:
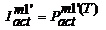 . (3.62)
. (3.62)
In primul caz, cand
profiturile anuale sunt constante, atunci:

Pentru cel de al doilea
caz, relatiile de calcul sunt:
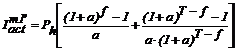 (3.64)
(3.64)
Efectuand calculele din
paranteza, se obtine aceeasi relatie de calcul a termenului
de recuperare.
Exemplu: Pentru
aceeasi situatie investitionala descrisa static de
datele din tabelul 3.3 si f = 3 ani,
calculul indicatorilor de eficienta, in acest caz, sunt:
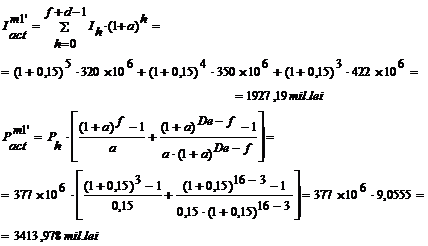
 lei profit final,
la 1leu investit.
lei profit final,
la 1leu investit.

D. Actualizarea la momentul scoaterii din functiune
a capitalului fix
Triunghiurile
actualizarii sunt prezentate in figura 3.11.
m0 m1 m2 timp

d De
I
P
Fig. 3.11. Schema de calcul
Investitiile
si profiturile actualizate la momentul m2
sunt calculate astfel:
 (3.65; 3.66)
(3.65; 3.66)
Cand profiturile anuale
sunt constante:
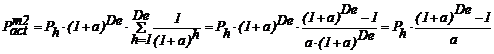 (3.67)
(3.67)
1. Randamentul economic actualizat:
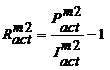 . (3.68)
. (3.68)
2. Termenul de recuperare a investitiei,
actualizat:
Pornind de la
relatia de baza:
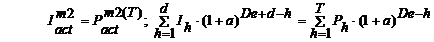
Cand
profiturile anuale sunt considerate constante:
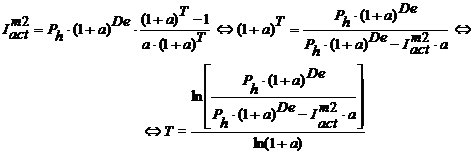 (3.69)
(3.69)
Exemplu: In cazul aceleasi
aplicatii, sintetizate static in tabelul 3.3, se calculeaza
randamentul si a termenul de recuperare actualizati, in momentul
punerii in functiune a obiectivului.

In conditiile reinvestirii profitului obtinut in urma
functionarii capitalului fix pus in functiune, a carei
valoare statica a fost de 1,112 mil.lei, intr-o activitate la care nivelul
eficientei economice este de 15%, se va realiza un capital insemnat, de
21003,2 mil. lei. Randamentul si termenul de recuperare
actualizati sunt:
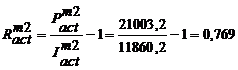 lei profit final, la 1 leu investit,
lei profit final, la 1 leu investit,
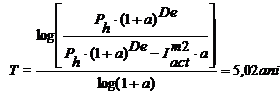 .
.




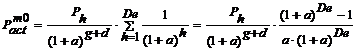
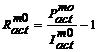 .
.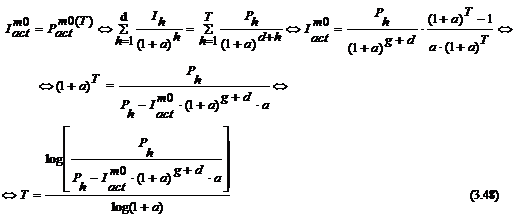
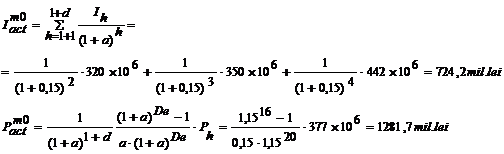
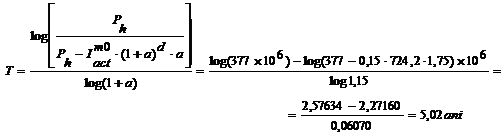
 ,
, 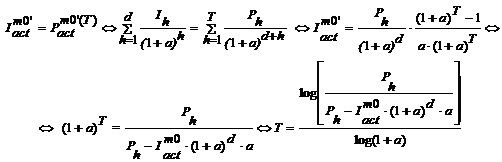
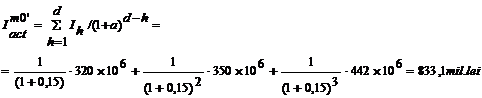
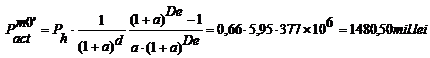


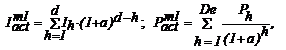
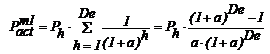
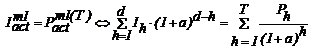 .
.
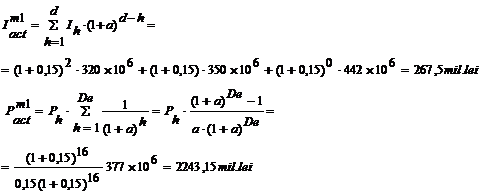
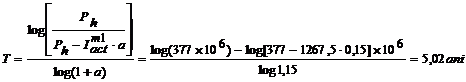


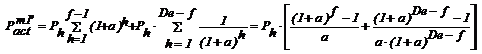


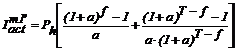
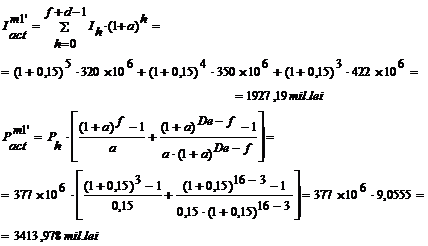
 lei profit final,
la 1leu investit.
lei profit final,
la 1leu investit.

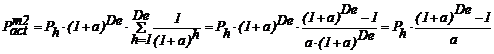 (3.67)
(3.67)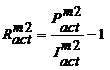 .
.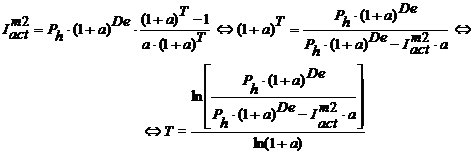 (3.69)
(3.69)
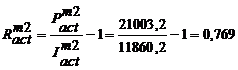
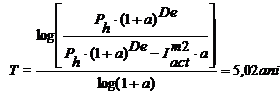 .
.