Binarizarea imaginilor

Binarizarea imaginilor

Majoritatea detectoarelor de fronturi produc o matrice de amplitudini a fronturilor dintr-o imagine. Valorile mari indica fronturi.

Multe metode de extragere a caracteristicilor din imagini folosesc o reprezentare binara a imaginii, obtinuta pe baza matricii de amplitudini a fronturilor. Astfel, daca a(k , l) este matricea amplitudinilor, atunci imaginea binara, B(k , l) este :

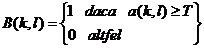unde T este o valoare prag.

Valoarea T poate fi aleasa inspectand histograma imaginii, a(k , l), astfel incat numai un mic procent din elementele matricei a sa aiba valoarea >= T. In acest caz, operatia de binarizare este globala, deoarece T este ales pe baza unei informatii globale si operatia se efectueaza peste intreaga imagine.

In multe cazuri imaginea contine regiuni cu proprietati statistice diferite. Binarizarea globala poate produce frontiere subtiri in unele regiuni si late sau intrerupte in altele. In aceste cazuri este de dorit o binarizare adaptata local, adica :

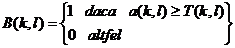
unde T(k,l) este pragul adaptat local. O metoda de a-l obtine consta in calculul mediei aritmetice locale in matricea amplitudinilor produsa de detectorul de fronturi :

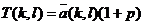, unde p este un procent care indica nivelul pragului peste media locala.

Deci, pragul difera de la pixel la pixel in functie de media amplitudinilor fronturilor din vecinatatea pixelului.

Transformata Hough : detectia liniilor drepte din imagini

Transformata Hough foloseste matricea B, obtinuta prin binarizarea matricei a a amplitudinilor fronturilor.

Fie o imagine de N₁xN₂ pixeli. Cea mai simpla abordare a determinarii liniilor drepte este de a gasi linii determinate de perechi de pixeli si apoi a gasi pixeli din imagine care apartin acestor linii. Numarul maxim de linii posibile este N(N-1) /2, unde N = N₁ x N₂. In cazul cel mai defavorabil, fiecare pixel este verificat daca apartine uneia dintre cele N(N-1) /2 linii. Deci, complexitatea calculului este O(N³), ceea ce face ca metoda sa nu poata fi aplicata in practica.

Transformata Hough utilizeaza o reprezentare parametrica a liniilor pentru reducerea complexitatii calculului cautarii lor in imagini :

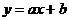
In spatiul parametric (a , b) fiecare linie este reprezentata printr-un singur punct (a , b).

Fie o linie care trece prin 2 puncte (x₁ , y₁), (x₂ , y₂) :

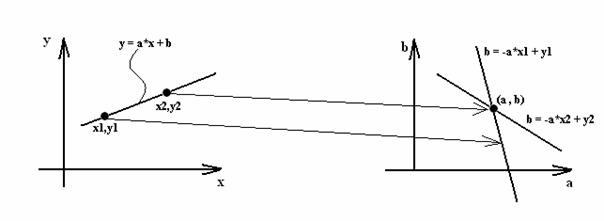
Liniile care trec prin (x₁ , y₁) se reprezinta in spatiul parametric prin linia b = - a*x₁ + y₁ iar cele care trec prin (x₂ , y₂) se reprezinta prin linia b = - a*x₂ + y₂ . Intersectia acestor 2 linii din spatiul parametric determina in mod unic dreapta care trece prin (x_i , y_i), i = 1, 2.

Pentru detectia liniilor drepte se poate proceda astfel :

Se discretizeaza spatiul parametric si se reprezinta printr-o matrice P, astfel incat P[i][j]

corespunde unui punct (a_j , b_i)

a₁<= a <= a_K , a_j = a₁ + j*da

b₁<= b <= b_L, b_i = b₁ + i*db

Se initializeaza elementele matricei P cu zero.

Pentru fiecare pixel (x, y), cu B(x , y) = 1

// se formeza ecuatia b = - a*x + y

pentru fiecare a₁<= a_m <= a_{k //}  ( a_m=a₁ + m* da)

b_m = - a_m*x + y

i = (b_m - b₁)/(b_L - b₁) * (L-1)

P[i][m] ++;

3. Pentru fiecare element al matricei P, P[i][j]

daca P[i][j] >= T atunci

// in imagine exista dreapta y = a*x + b, unde a = a₁ + j* da, b = b₁ + i*db

P[i][j] - numara intersectiile liniilor care trec prin (a , b) si indica numarul de pixeli care satisfac ecuatia

y = a*x + b.

Precizia metodei depinde de pasul de discretizare a spatiului (a , b), deci de marimea matricei P.

Complexitatea calculului transformatei Hough este O(k*N), unde k este numarul de subintervale pe axa a iar N este numarul de pixeli din imaginea de intrare.

Utilizarea ecuatiei parametrice y = a*x + b produce dificultati in reprezentarea liniilor verticale  ( a-> ∞).

O reprezentare mai buna este reprezentarea polara :

r = x* cos( ) + y* sin(

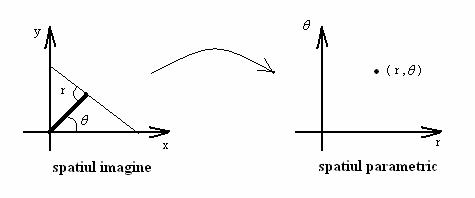
O linie care trece prin (x₁ , y₁) reprezinta o curba sinusoidala, r = x1* cos( ) + y1* sin(

in spatiul parametric (r, θ).

Puncte colineare, (x_i , y_i), din imagine, corespund intersectiilor sinusoidelor din spatiul parametric.

Deci, punctele de intersectie definesc liniile drepte din imagine.

Pentru o imagine de N₁xN₂ pixeli,

.

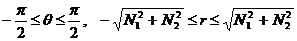Discretizarea spatiului parametric :

- intervalul 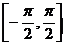se imparte in n subintervale;

- intervalul [ -D, D ] se imparte in m subintervale, unde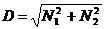

Fie P[n][m] matricea in care se memoreaza punctele grilei spatiului parametric.

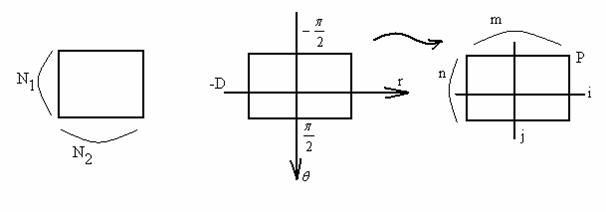
pentru =>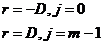

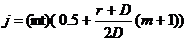
pentru =>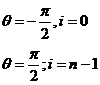

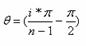
Se prelcalculeaza valorile functiilor sin si cos pentru valorile discrete ale lui :

float *COS, *SIN, t;

for ( i=0; i<n; i++)

Implementarea transformatei Hough

void Hough(imagine B,//matricea binara a amplitudinilor

int P[N][M],

int n, int m,

int N₁, int N₂

float *COS , float *SIN,

int T,

imagine out

}

//Se calculeaza transformata Hough inversa (din spatiul (r , θ) in (x , y))

//Pentru fiecare element P[k][l] > T, se inscrie in matricea out, sub forma de pixeli = 1, //linia dreapta corespunzatoare elementului (k , l)

//Se efectueaza operatia and intre rezultatul transformatei si matricea de intrare

for(k = 0 ; k < n ; k++

for(l = 0 ; l < m ; l++)

}

}

Anumiti detectori de fronturi produc nu numai marimea frontului ci si directia frontului, Φ(x , y).

Informatia directionala poate fi utilizata pentru a reduce calculele in transformata Hough.

Astfel, diferentiind in raport cu x ambele parti ale ecuatiei :

r = x* cos( ) + y* sin(

rezulta: 

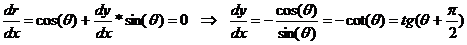
Directia frontului in (x , y) este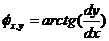

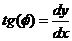
Deci :

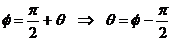
Rezulta ca pentru fiecare pixel B[k][l] = 1, numai un singur element al matricei P trebuie sa fie actualizat : P[i_θ][j_θ], unde :

= FI[k][l], - FI este matricea directiei frontului

i (θ/п + 0.5)(n-1)

r = l* COS[i ] + k* SIN[i

j_θ = (int) r

Complexitatea calculului transformatei Hough se reduce ]n acest caz de la O(k*N) la O(N).

Transformata Hough se poate generaliza pentru a detecta orice curba parametrica. Metoda este practica numai pentru curbe cu un numar mic de parametri. De exemplu, pentru cerc :

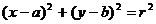
parametrii sunt r, a , b. Este necesara o matrice P tridimensionala, P(r , a , b).
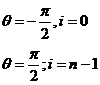