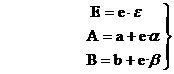Functii incomplet specificate
f : Sn → S1
complet specificata daca valoarea logica a acesteia este
cunoscuta pentru fiecare din cele 2n pct ale lui f.
cunoastem f
pentru 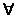 Pj
Pj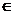 Sn
Sn
incomplet specificata = nu are o valoare logica
specificata pentru o submultime de pct a sp . Sn.
Decodificator de cifre
zecimale afisate prin 7 segmente (cristale lichide, Led-uri)
Display cu 7
segmente creeaza cifra 8.
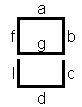 aprinderea ∕ stingerea unui segment
~ de ce vrem sa afisam
aprinderea ∕ stingerea unui segment
~ de ce vrem sa afisam
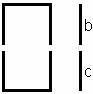
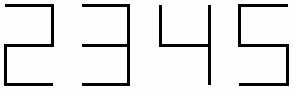
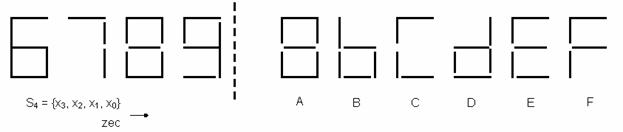
Se va proiecta setul celor 7 functii a, b, c, d, e, f, g :
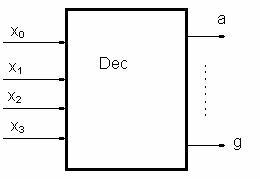
1. Regula: Atunci cand un segment e aprins fct = 1;
stins fct = Ø;
In functie de cele 4 intrari putem genera alte forme ale
desenului cifrei respective.
2. Daca avem A, B, C, D, nu are voie.
3. Sa se reproiecteze functia astfel
incat o comb. de intrare nepermisa (10-15) in b10
sa fie identificata de catre circuitul nostru.
Desenul vi-l propuneti singuri (seminar) de exemplu 10
betisorul de sus.
4. Sa se reproiecteze
pentru a decodifica cifrele hexa:
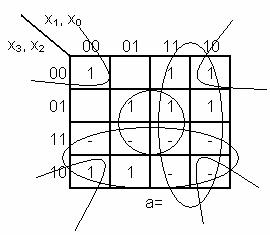
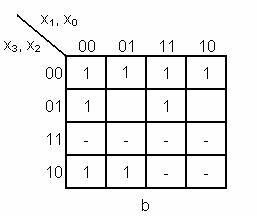
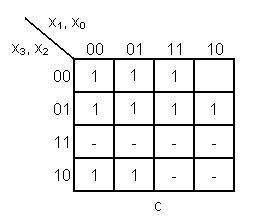
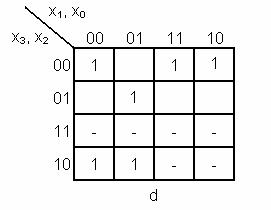
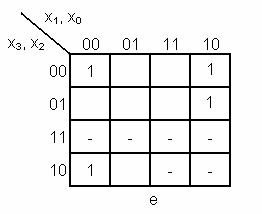
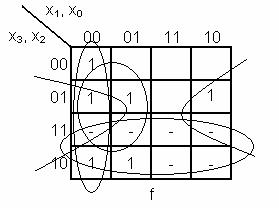
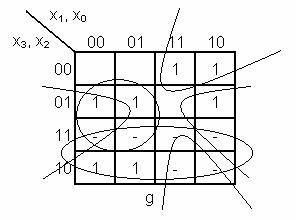
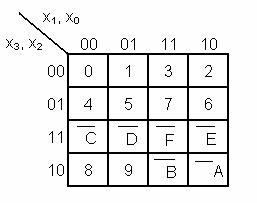
- functiile incomplet specificate f = 0,1 in cazul in care avem siguranta ca
valori superioare lui 9 nu pot aparea.
Exemplu temperatura:
- afis semn
- afis pe 2 cifre val
valori inferioare -30 n+au cum sa apara
un sistem de afisare a temperaturii masutate din grad in grad
valoarea absoluta pe 7 biti, semnul cel de al 8-lea.
Daca lucram in C2 val
nu in C2
± 0
don't care value
Proiectarea acestor functii in forma minimala
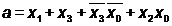
punem
ce-I comun
Am utilizat valoarea don't care
presupunind ca in acele pct functia logica ar avea valoarea 1
pentru a obtine termeni cat mai simpli; am prelungit domeniul de definire al functiei.
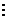
‼ ‼
g = x3+ x2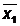 + x2
+ x2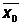 +
+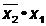
1) Sa se termine toate functiile
2) Sa se descopere termenii reutilizabili
Sa se deseneze circ. complet utilizand module MAHD
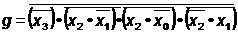
5. Considerand terminata proiectarea se va face un bilant cu
porti MAHD pe tipuri si se va termina complexitatea nr. module x
numar intrari
se va comp. economia cu termeni canonici
Este de 1-ri avem nevoie 1 logic = prod. pe 4 biti.
Proiectarea comparatoarelor de marime
Proiectarea sumatoarelor
Performante de raspuns

O celula de comparator de marime trebuie sa fie
caracterizata de urmatoarele intrari/iesiri.
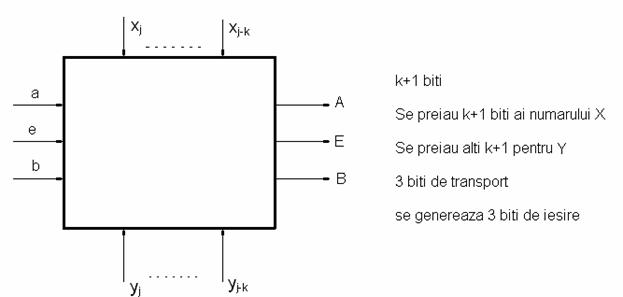
k=1 → 2 biti comp. pe 2 biti
k=0 → 1 bit comp. pe 1 bit
Marimile a, e, b vor fi denumite transp. de intrare pentru literele
mici
transp. de iesire pentru literele mari
X, Y canal x, y
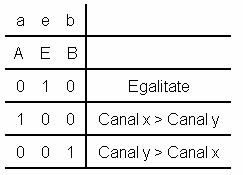
Semnificatiile intrarilor sosesc de la stanga la dreapta.
modul de actiune ale unui astfel de modul care utilizeaza k+1
biti e modul serial de propagare a informatiei.
x7 . . . x1
y7 . . . y1
y7 ≥ x7 bit 6 isi prelucreaza
informatia si stie ca x=y are conf. si din stg.
Daca vom considera un timp de propagare tp de la intrarea fiecarui
modul pana la iesire constatam ca un rezultat stabil in
timp se va obtine dupa n tp, unde n este numarul de celule
inseriate puse una dupa alta. Cu cat raspunsul se obtine mai
repede la iesire cu atat circ. e mai performant.
Comp. nr. pe 32 biti magnitude comparator.
Daca tipul de propagare al informatiei este tp daca e bit
avem nevoie de 32 intervale intarziere tp x 32.
k = 0
k = 1 comp. pe 2 biti intervalul e la 32/2=16 tp
k = 3 comp. 32/3=11 biti
k = 4 8 tp
k = 8 32/8=4 tp
tp = 1 ns
Rezolvarea problemelor prin
conlucrare in paralel. Comparator de
1 bit / 2 biti.
Comparatorul pe 3 biti:
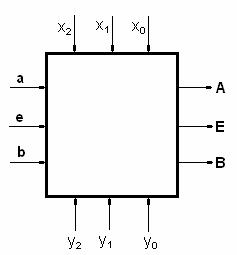
α = 1 daca
>
β = 1 daca
<
ε = 1 daca
=
In acest caz: 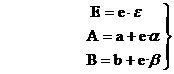
ε = Comb.
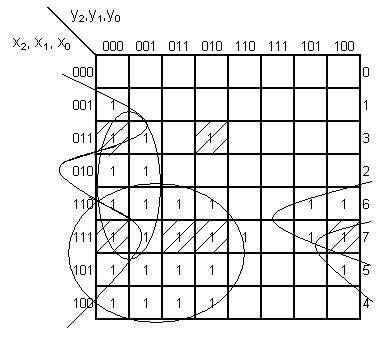
α = 1
daca x2x1x0 >
y2y1y0
Forma partiala:
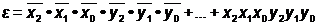
α = 28
β = 28
ε = 8
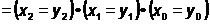
XoR negat = coincidenta
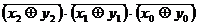
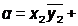 (1 - -) > (0 - -)→ min x4 >
(1 - -) > (0 - -)→ min x4 >
max
y3
4 > 3
ordinea incercuirilor nu conteaza
x2 = 1 e comun
y2 = 0 e comun
val. min x = 4
val. max y = 3
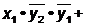 (- 1 -) > (0 0 -)→2>1
(- 1 -) > (0 0 -)→2>1
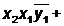 (1 1 -)
> (- 0 -)→6>5
(1 1 -)
> (- 0 -)→6>5
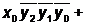 (- - 1) > (0 0 0)→1>0
(- - 1) > (0 0 0)→1>0
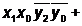 (- 1 1) > (0 - 0)→3>2
(- 1 1) > (0 - 0)→3>2
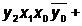 (1 1 1) > (- - 0)→7>6
(1 1 1) > (- - 0)→7>6
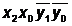 (1 - 1) >
(- 0 0)→5>4
(1 - 1) >
(- 0 0)→5>4
nr. x = 3,7 > 0,2
Concept de indifferent → rational
Obs: in α biti
x apar in mod direct
y numai negati
Cum se extrapoleaza /
diagrama de 4x4
= 4x4
biti 16 coloane, 16 linii pe diag.
16 cazuri egalitate
256-16 = 240 pct 1>0
120 pct x>y 15>14 120 pct acop in 15 cazuri
Comp. direct pe 8 biti
pe 16 biti→ 216 combinatii
nr. sunt de 8 biti →
256x256 diag. k
28 = 256 egalitate
215-27=
255 cazuri
Pentru un comp. pe 33 biti → 11 celule
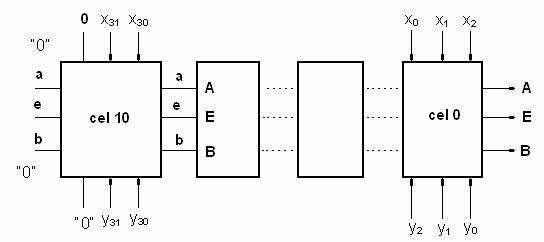
Concluzia: tp ~ complexitatea unei celule


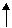 conform
formulei A=a+e·α
conform
formulei A=a+e·α

asteptare se
prelucreaza rapid
impune asteptare var
locale
Sumatoare binare
Un S.B. complet are 2 tipuri var intrare: grupurile de biti din structura binara a celor
2 operanzi (x, y) si 1 bit numit transport de intrare.
Iesiri: fiecare sumator genereaza rasp. ∑ pe cati
biti apar la intrare si 1 bit de transport pentru celula de rang
superior.
Sumator complet pe 1 bit.
 Sumatorul
pe 2 biti
Sumatorul
pe 2 biti
Sumatorul pe 1 bit
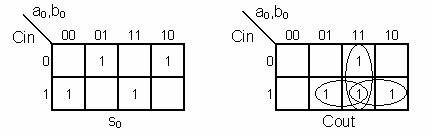
S = 1 cand numarul de biti <1 se insumeaza =
impar
Transport cand nr. bit =1≥2,3
forma disjunct care nu este
minimizabila
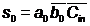 +
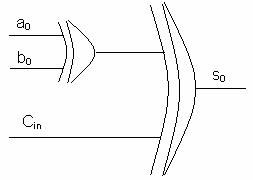
desenul cu porti NAND s0 → info
+
desenul cu porti NAND s0 → info
+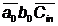 se propaga prin 3 nivele 1 Nand =
se propaga prin 3 nivele 1 Nand = 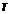
+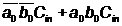 1, 2, 3
nivele NAND
1, 2, 3
nivele NAND

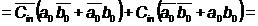
XoR negat
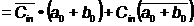
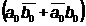 → XoR = suma modulo
2
→ XoR = suma modulo
2
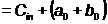
transportul: Cout =a0b0+a0Cin+
b0Cin
tp = 3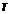 ,
, 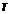 = tp per poarta
= tp per poarta
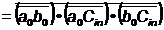
tp = 2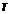
Concluzie:
trecerea informatiei din
telefonul fara fir de la 1 celula la alta ce ne impiedica.
Sumatorul binar pe 2 biti:
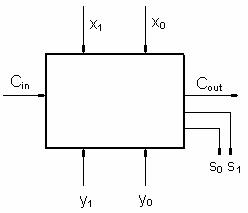
Functiile C1, Cin ~ cei toti 5 biti
8 coloane; 4 randuri
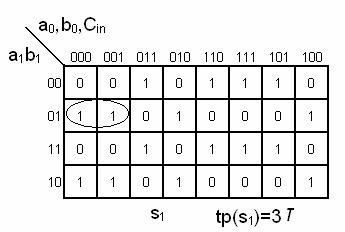
nr. par de 1 cel putin 2 de 1
s1
= ?
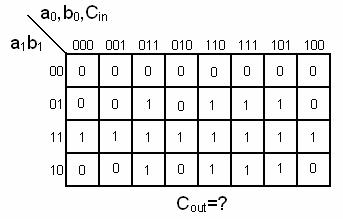
Expr. acestei fct.=?
Toti bitii apar nenegati
acasa
tp (Cout) = 2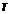
S pe 32 biti suma e de 2 ori mai scurt care se propaga rapid.