Dreapta - Probleme
1. Fie dreapta oarecare (D) (d,d ,d') definita de punctele A
si V . Sa se
construiasca proiectiile dreptei (D)
si proiectiile urmelor sale; sa se determine traseul dreptei
(D). A(60,50,10) V(20,0,30).
2. Fie dreapta oarecare (D) (d,d ,d') definita de punctele A
si B . Sa se
construiasca proiectiile dreptei (D)
si proiectiile urmelor sale; sa se determine traseul dreptei
(D).
A(17,
42, 5 ) I
I1 si B(-45,- 5, 23 ) I I2.
3. Se considera dreapta (D) definita de
punctele A si B.
Prin punctul I(20,yD,zD)
situat pe dreapta (D), sa se
construiasca dreapta orizontala (D1)
care face cu planul lateral [L] un unghi de 30o.
A(10,
77, 12 ) I
I1 si B(-25, 32, 10) II2.
Sa se
construiasca orizontala (O)=(AB)
concurenta cu frontala (F)=(AC)
.
A(70,
20, 15), B(10, 52, zB) si C(50, 20, 35) .
5. Sa se construiasca dreptele
concurente (D1)=(AB)
si (D2)=(AC). A(65, 20, 10), B(80, 30, -5) si C(15, 50, 10) . Ce dreapta este
(AC)?.
6. Prin punctul A(40, 30, 20) sa se
construiasca o frontala care face un unghi de 45o cu planul
[H]. Sa se construiasca un segment AB pe frontala de 40 mm. In
punctul A sa se ridice o drepta (D) perpendicula pe
frontala.
7. Prin punctul A(50, 35, 25) sa se
construiasca o orizontala care face un unghi de 30o cu planul
[V]. Sa se construiasca un segment AB pe orizontala de 40 mm. In
punctul A sa se ridice o drepta (D) perpendicula pe
orizontala.
Fie punctul A(40,30,20). Sa se duca prin A o Orizontala
(O) ce formeaza un unghi de 45o cu planul [V] si o
frontala (F) ce formeaza un unghi de 60o cu [H]. Sa
se construiasca triunghiul
ABC dreptunghic in B astfel ca AB = 45
mm, BI
(O) si punctul C I
(F).
Fie punctul A(40,30,20). Sa se duca prin A o frontala (F) ce
formeaza un unghi de 45o cu planul [H] si o
orizontala (O) ce formeaza un unghi de 60o cu [V]. Sa
se construiasca triunghiul
ABC dreptunghic in B astfel ca AB = 45
mm, BI
(O) si punctul C I
(F).
10. Sa se construiasca o dreapta
frontala (F) perpendiculara
pe o dreapta oarecare (D) definita
de punctele A si B intr-un punct
M(-10,yD, zD)
al acesteia.
A(17,
42, 25) si B(-35,45, 15).
11. Fie punctul N(30, yD, zD)
situat pe o dreapta (AB); Prin
punctul N sa se
construiasca o dreapta de profil (D1),
perpendiculara pe (AB).
A(20,
18, 35) si B( 40, 35, 15).
12. Sa se construiasca un triunghi
isoscel ABC, avand laturile //AB//=//AC//=30
mm si sa se determine centrul de greutate G al acestuia.
A(35,
20, 40) (AB) frontala, (AC) orizontala.
Indicatii:
Prin A
se construiesc o
frontala (AB) si o orizontala (AC) concurente, pe care se pot masura
adevaratele marimi ale laturilor congruente. Centrul de greuate G se
afla la intersectia medianelor /NC/
si /MB/.
Fie dreapta frontala (F) definita de punctele A (
90,30,0) si L(0,30,75). Prin punctul M(20,55,20) sa se
construiasca perpendiculara pe (F).
Fie punctul A(40,30,20). Sa se duca
prin A o orizontala (O) ce formeaza un unghi de 45o cu
planul [V] si o frontala (F) ce formeaza un unghi de 60o
cu [H]. Sa se construiasca triunghiul ABC dreptunghic in B astfel ca AB = 45 mm, BI
(O) si punctul C I
(F).
Prin
punctul C(15,20,35) sa se construiasca perpendiculara pe dreapta
definita de punctele A(90,15,25) si B(25,55,25).
Sa se construiasca urmele planului [P] definit de frontala
(F), perpendiculara in punctul A pe dreapta oarecare (D)=(AB),
A(30, 5, 25) si B(10, 35, 0).
T planul [P] definit de Px(95,0,0), Py(0,60,0),
Pz(0,0,100). Punctele A(50, 20, zA), B(30,yB,20), C(20,0,zC) apartin
planului. Sa se construiasca triunghiul ABC in planul [P].
T Sa
se construiasca perpendiculara din punctul M (35, 30,25), pe planul [P] de capat, definit de Px(80,0,0), A(0,0,70). Sa se
determine punctul de intersectie I
.
Sa se
intersecteze planul [P] Px(80,0,0), H(0,70,0), V(0,0,60) cu un plan de nivel [R] cu z=40.
Sa se
construiasca dreapta de intersectie.
Sa se
determine adevarata marime a segmentul /AB/, A(50, 10, 15), B(10,35, 50), prin metoda rotatiei si
rabaterii. Sa se costruiasca triunghiul echilateral ABC in planul de capat [P],
definit de dreapta (AB).
Sa se construiasca sectiunea rezultata din
intersectia dintre o piramida dreapta ABCS cu baza in planul orizontal de proiectie si un
plan [P]
de capat. Sa se
determine adevarata marime a sectiunii si sa se desfasoare poliedrul
rezultat. Se dau A(70, 30, 0), B(40, 40,
0), C(55, 10, 0), inaltimea piramidei h=60mm, Px(15, 0,
0), M(60, 0, 30)I[P].
Sa se sectioneze un cilindru circular drept cu baza intr-un plan
de proiectie [V], un cerc cu
centrul in O1 si raza
R1, cu un plan vertical [P] (Px,M)=>
Px(35, 0, 0), M(90, 60, 0). Inaltimea cilindrului este de 70 mm . Cilindrul are centrul
bazei in O1(60, 0, 40), R1=25
mm.
Sa se construiasca, in adevarata marime,
sectiunea rezultata, desfasurata cilindrului si a
trunchiului de cilindru.
Sa se sectioneze un con circular drept cu baza, in planul orizontal de proiectie, un cerc
cu centrul O1(60, 40, 0)
si raza R1=25 mm, cu un plan proiectant [P], Px(20, 0, 0), M(80, 0, 50), plan de capat.
Varful conului este S(60, 40, 65).
Sa se determine adevarata marime a sectiunii si
sa se desfasoare trunchiul de con situat sub planul [P].
1 Urmele planului definit de punctele:
I) A( ), B(10, ) si C(
II)A(70, 20, 15),
B(10, 52, 15) si C(50, 20, 35)
Ce drepte se obtin?
a) Se traseaza dreptele;
b) Se definesc urmele dreptelor;
c) Se traseaza urmele planului.
2 Constructia triunghiului isoscel definit de:
a) A( frontala (F) si orizontala (O)
AI (F), AI (O) <(F)[H]=60, <(O)[V]=45.
b) Punctele B si C unde |AB|=|AC|=40
BI (F), CI (O),
3 Fie dreapta (AB):
A(2 , 35) si B( 4
a)
Sa se construiasca planul [P] ce contine dreapta
(AB);
b)
Din punctul M(70,50,70) sa
se duca o dreapta
perpendiculara la planul [P];
c) Care este punctul I de intersectie a dreptei cu planul?
I) [P] de capat II) [P] vertical.
Prisma dreapta
cu baza un triunghi echilateral A(70,35,0) B(45, 10,0) h=55
[P] plan de capat Px(5,0,0) M(75,0,40)
Fie prisma patrulatera dreapta [ABCA1B1C1] cu baza un triunghi echilateral [ABC] I [H]
si inaltimea / AA1 /=55
mm, A(70,35,0) B(45, 10,0) h=55
Prisma se intersecteaza cu planul [P], plan de capat Px(5,0,0) M(75,0,40).
Se cer :
1 Constructia prismei;
2 Constructia planului [P];
3 Sectionarea prismei cu planul de capat, constructia
sectiunii;
4 Rabaterea planului [P] pentru adevarata marime a
sectiunii;
Sa se
desfasoare poliedrul rezultat prin sectionarea piramidei cu planul de capat [P]


Fie piramida
patrulatera dreapta [VABC]
cu baza un triunghi echilateral [ABC] I [H] si inaltimea / VG /=55 mm, A(70,35,0), B(45, 10,0) si h=55.
Piramida se intersecteaza cu planul [P], plan de capat definit
de Px(5,0,0) M(75,0,40).
Se cer :
1 Constructia piramidei;
2 Constructia planului [P];
3 Sectionarea piramidei cu planul de capat, constructia
sectiunii;
4 Rabaterea planului [P] pentru adevarata marime a
sectiunii;
Sa se
desfasoare poliedrul rezultat prin sectionarea piramidei cu planul de capat [P] .
Sa se construiasca piramida [SABCD] cu baza ABCD I[P], unde
Px(60, 0, 0) si M(0,65,0),
A(40,yA,5 I[P]
//AB//=25 mm, //AD//=40 mm,
//SW//=50 mm, /AB/I(D1) si /AD/ I(D2)
(D1)-dreapta orizontala si (D2)-dreapta
verticala

Sa se
construiasca in planul de capat [P]
determinat de punctele A(45,10,35),
B(35,30,40) un patrat [ABCD].
Sa se construiasca prisma
dreapta cu baza [ABCD] si de inaltime h=60 mm. Sa se intersecteze prisma cu un plan de nivel z=50
mm.
Sa se desfasoare prisma rezultata in urma
intersectiei.
Se parcurg etapele:
1 Constructia planului [P];
2 Punctele A si B;
3 Rabaterea planului ȋn planul [H], definirea patratului
ȋn adevarata marime;
4 Ridicarea rabaterii, pentru punctele C, D;
5 Construirea prismei pornind de la muchiile din plan [V] frontale, cu
lungime de 60;
6 Vizibilitatea prismei;
7 Desenarea planului de nivel, definirea punctelor de intersectie dintre
planul [N] si piramida.
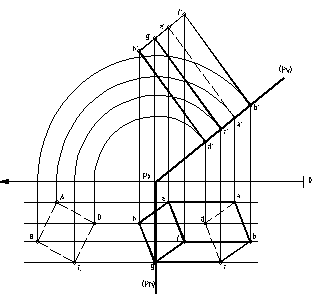
Se se construiasca epura unei piramide dreapte [ABCS] cu baza un triunghi echilateral [ABC] I[P] (Px,
A), centrul cercului circumscris bazei este GI[P] si inaltimea piramidei //GS//=60
mm. Sa se intersecteze piramida cu un plan [R],
[R]//[P] aflat la distanta d de acesta. Sa se
desfasoare trunchiul de piramida rezultat in urma
intersectiei. (tabelul
4.13).
Modelul de rezolvare este pentru varianta nr. 12 (fig.4.26
a,b):
Px( [P] plan de capat, A(125, 65, 60), G(110, 40, zG), d=30
mm
|
Nr.
|
[P]
|
[P]
|
d
|
|
Px
|
A
|
G
|
|
xPx
|
xA
|
yA
|
zA
|
xG
|
yG
|
zG
|
|
80
|
125
|
60
|
65
|
110
|
yG
|
40
|
Vertical
|
45
|
|
30
|
60
|
25
|
60
|
105
|
yG
|
55
|
Vertical
|
30
|
|
30
|
100
|
55
|
20
|
105
|
yG
|
55
|
Vertical
|
30
|
|
20
|
40
|
15
|
40
|
65
|
yG
|
25
|
Vertical
|
40
|
|
|
95
|
15
|
50
|
110
|
yG
|
|
Vertical
|
45
|
|
60
|
40
|
40
|
20
|
20
|
yG
|
20
|
Vertical
|
30
|
|
20
|
65
|
65
|
60
|
50
|
40
|
zG
|
Capat
|
40
|
|
20
|
60
|
30
|
35
|
45
|
40
|
zG
|
Capat
|
30
|
|
20
|
35
|
25
|
25
|
45
|
40
|
zG
|
Capat
|
30
|
|
|
95
|
50
|
15
|
110
|
40
|
zG
|
Capat
|
40
|
|
|
|
|
|
|
|
zG
|
Capat
|
35
|
|
|
|
|
|
|
|
zG
|
Capat
|
30
|
Indicatii:
Se determina planul [P] punctul G si se rabat planul [P] si
punctele A si G in planul [H] unde se
construieste triunghiul echilateral A0B0C0 inscris in cercul de centru R ce trece prin A cu centrul in G. Se ridica rabaterea si se construieste inaltimea piramidei
intial in planul [V] de 60 mm. Inaltimea piramidei este
perpendiculara pe urmele planului [P]. Se construiesc proiectiile
muchiilor piramidei, avandu-se in vedere vizibilitatea lor si urmele
planului [R], paralele cu urmele planului [P]. Se definesc
proiectiile [1'2'3'] si [123] triunghiului de
intersectie a piramidei cu planul [R]. Pentru construirea
desfasuratei piramidei este necesara cunoasterea dimensiunilor muchiilor.
Se roteste muchia (AS) in jurul lui S pana ce devine o
frontala (A1S1) , segmetul de frontala /a'1s'1/ defineste valoarea reala a
muchiilor. Desfasurata se construieste pornind de la triunghiul
echilateral [ABC] si construind initial fetele laterale ale
piramidei. Segmentul /S 1/ =/1'1s'1/
se gaseste in adevata marime pe frontala (A1S1).

Fig. 4.26, a

Fig. 4.26, b
Se se construiasca epura unei prisme dreapte [ABCA1B1C1] cu baza un triunghi
echilateral [ABC] I[P] (Px,
A); [P] plan vertical, centrul cercului circumscris bazei este GI[P] si inaltimea prismei h=80
mm. Sa se intersecteze prisma cu un plan [R], [R]//[V] aflat la
distanta d de acesta. Sa se desfasoare
trunchiul de prisma rezultat in urma intersectiei. (tabelul 4.14).
Modelul de rezolvare este pentru
varianta nr. 12 (fig.4.27 a,b):
Px(30, 0, 0) si A(60, 25, 60), B(100, xB, 20), d=80
Tabelul
4.14
|
Nr.
|
[P]
|
[P]
|
d
|
|
Px
|
A
|
B
|
|
xPx
|
xA
|
yA
|
zA
|
xB
|
yB
|
zB
|
|
50
|
30
|
40
|
25
|
10
|
10
|
zB
|
Capat
|
70
|
|
50
|
20
|
10
|
35
|
35
|
45
|
zB
|
Capat
|
80
|
|
30
|
15
|
45
|
20
|
0
|
15
|
zB
|
Capat
|
60
|
|
0
|
20
|
60
|
25
|
60
|
10
|
zB
|
Capat
|
60
|
|
|
|
|
|
|
50
|
zB
|
Capat
|
80
|
|
|
|
|
|
|
20
|
zB
|
Capat
|
70
|
|
50
|
30
|
25
|
40
|
10
|
yB
|
10
|
Vertical
|
70
|
|
50
|
20
|
35
|
10
|
35
|
yB
|
45
|
Vertical
|
80
|
|
30
|
15
|
20
|
45
|
0
|
yB
|
15
|
Vertical
|
60
|
|
0
|
20
|
25
|
60
|
60
|
yB
|
10
|
Vertical
|
60
|
|
|
|
|
|
|
yB
|
50
|
Vertical
|
80
|
|
|
|
|
|
|
yB
|
20
|
Vertical
|
70
|
Indicatii:
Se determina planul [P], punctul B, continut in
planul [P] si se rabat planul [P] si
punctele A si B in planul [H] unde se
construieste triunghiul echilateral A0B0C0 Se ridica rabaterea pentru
punctul C (c,c') si se construiesc muchiile prismei (segmente pe
orizontale), perpendiculare pe urmele planului [P] de 80 mm,
intial in planul [H], avandu-se in vedere vizibilitatea lor. Se
construieste urma (Rh) a planului [R], paralela
cu (Ox). Se definesc
proiectiile [1'2'3'] si [123] triunghiului de
intersectie al prismei cu planul [R]. Pentru construirea
desfasuratei prismei este necesara cunoasterea dimensiunilor muchiilor.
Muchiile prismei sunt segmente de frontala, valoarea reala a muchiilor fiind
de 80 mm in planul [H]. Desfasurata se construieste pornind de
la triunghiul echilateral [ABC] si de la fetele laterale ale
prismei. Segmentul /A 1/ =/a1/
se gaseste in adevata marime pe orizontala (AA1).
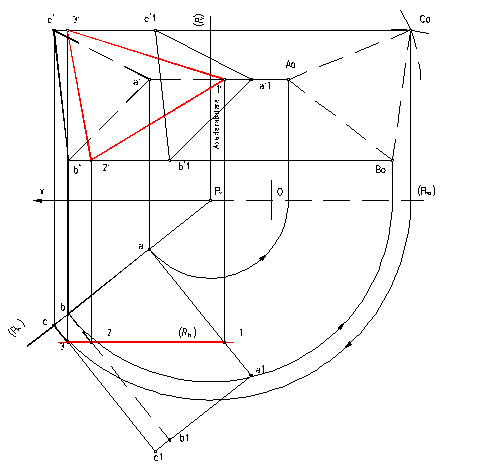
Fig. 27,a

Fig. 27,b











