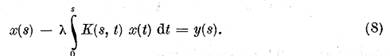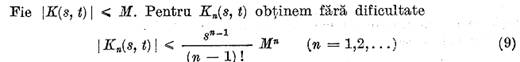 |  |
|
Ecuatia de tip Volterra
Daca nucleul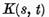 
se anuleaza pentru 
atunci ecuatia (1) poate fi scrisa
sub forma
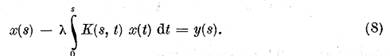
Ecuatiile de acest tip se numesc ecuatii integrale Volterra.
Este usor de verificat ca
nucleele iterate ale ecuatiei Volterra de asemenea se anuleaza
pentru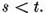 
Presupunand ca nucleul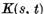 
este continuu pentru 
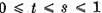vom demonstra ca dezvoltarea (4) este
adevarata pentru orice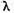 
complex adica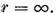 
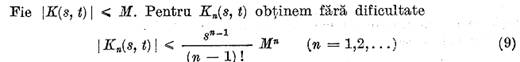
Intradevar pentru 
marginirea este trivial
satisfacuta si daca (9 este adevarata pentru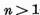 
atunci
de unde
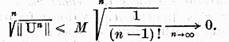
Rezulta in acest mod ca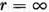 
si ca un
operator integral de tip Volterra nu are valori caracteristice.
Acest document nu se poate descarca
| E posibil sa te intereseze alte documente despre:
|
| Copyright © 2024 - Toate drepturile rezervate QReferat.com | Folositi documentele afisate ca sursa de inspiratie. Va recomandam sa nu copiati textul, ci sa compuneti propriul document pe baza informatiilor de pe site. { Home } { Contact } { Termeni si conditii } |
Documente similare:
|
Cauta document |