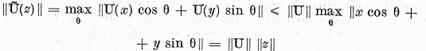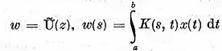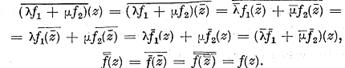Ecuatii in spatiul complex

Ecuatii in spatiul complex

Dupa cum va fi clar din ceea ce urmeaza este natural sa consideram ecuatia

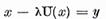
in spatiul complex, in particular, dandu-i lui 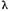valori complexe. In legatura cu aceasta , vom introduce mai jos unele notiuni ajutatoare , referitoare la spatiile complexe si care permit includerea cazului real in cel complex.

1.Complexificatul spatiului Banach X

Fie Z un spatiu normat complex . Vom spune ca Z are o structura reala daca pe Z este definit un operator C numit involutie , care aplica pe Z in el insusi si are urmatoarele proprietati :

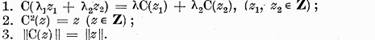
Multimea elementelor pentru care 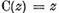se numeste nucleu real al spatiului Z si se noteaza Re Z; elementele acestei multimi se numesc reale.

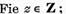elementul :

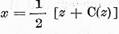
se numeste parte reala a elementului z si se noteaza x=Re z.

Elementul :

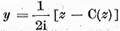
se numeste partea imaginara a elementului z si se noteaza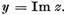

Deoarece :

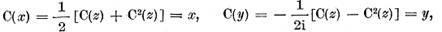
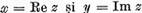sunt elemente reale. Evident

si

Ultima relatie justifica sa numim elementul 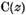conjugatul elementului z si sa introducem notatia obisnuita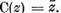

Daca elementul z admite o reprezentare sub forma 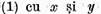reali atunci neaparat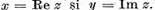

Intr-adevar 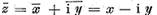si de aceea

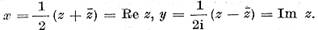
Astfel reprezentarea (1) este unica , elementele x si y sunt determinte univoc de elementul z.

Nucleul real X al spatiului Z este spatiu normat real si daca spatiul Z de plecare este complet X este de asemenea complet.

Intradevar o combinatie liniara cu coeficienti reali de elemente din X este si ea element al multimii X. Faptul ca in X sunt satisfacute axiomele spatiului normat rezulta din faptul ca aceste axiome sunt satisfacute in spatiul dat Z.

Sa probam completitudinea lui X . Fie 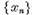un sir fundamental de elemente din spatiul X . Considerandu-l in spatiul Z si tinand seama de completitudinea acestuia , gasim ca exista.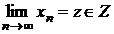

Deoarece in virtutea conditiei 1 ,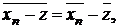 avem 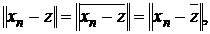  de unde 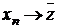.Din unicitatea limitei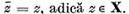

Toate spatiile reale concrete considerate mai sus sunt nuclee reale ale unor spatii complexe corespunzatoare . Astfel de exemplu 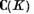real este nucleul real al spatiului complex 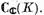Aici involutia va fi operatorul de conjugare complexa 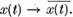Acelasi lucru poate fi spus in legatura cu spatiile 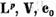etc.

In general un spatiu real arbitrar X poate fi considerat ca nucleu real al unui spatiu complex anume ca nucleul real al spatiului Z ale carui elemente sunt perechile ordonate de elemente ale spatiului X ;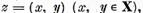iar operatiile cu ele sunt introduse dupa regulile urmatoare :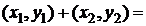

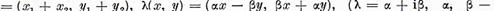
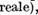
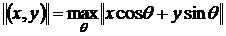(2)

Pentru a ne convinge ca X este nucleul real al spatiului Z este suficient sa punem

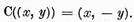
Atunci in spatiul Z vor fi reale toate elementele de forma (x, 0) si numai ele.

Deoarece

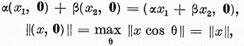
vom obtine rezultatul dorit identificand elementul (x, 0) cu elementul x. Aceasta identificare permite ca in locul lui ( x, y) sa folosim notatia obisnuita x+i y. Spatiul Z se numeste complexificatul lui X.

2.Operatori liniari si continui intre spatii complexe

Fie Z si W spatii complexe cu nucleele reale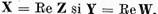

Un operator liniar continuu U care aplica pe Z in W se numeste real daca trece elementele reale ale spatiului Z in elemente reale ale spatiului W, adica daca 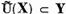; un operator real induce astfel un operator liniar continuu din spatiul real X in spatiul real Y.

Reciproc daca U este operator liniar continuu care aplica spatiul X in spatiul Y si daca 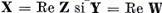atunci punand

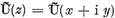=U(x) + iU(y) (z=x+i y)

obtinem un operator liniar continuu 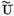din spatiul complex Z in spatiul complex W. Evident pe X operatorul U coincide cu U. Operatorul 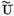se numeste extensia complexa a operatorului U.

Sa remarcam integralitatea

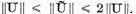   (3)

Prima parte a integralitatii este evidenta. A doua parte rezulta din lantul de integralitati

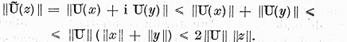
(Aici a fost folosita integralitatea 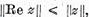care se demonstraza astfel :

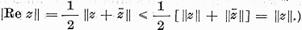
Intr-o serie de cazuri se poate demonstra egalitatea 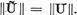Astfel daca normele in spatiile Z si W sunt definite prin formula (2) atunci

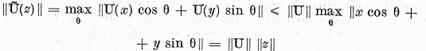
si prin urmare 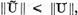care impreuna cu (3) da

Atunci daca pentru orice 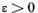exista un element real si normat x astfel ca

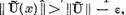de asemenea deoarece in acest caz

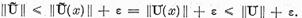
Ultima conditie este satisfacuta, de exemplu, cand Z si W sunt spatii de functii dintre cele enumerate mai sus iar operatorul 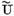este operatorul integral

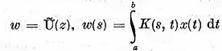
cu nucleul real K (s, t).

Exact la fel ,conditia este indeplinita daca Z si W sunt spatii de siruri, iar operatorul 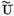este definit de o matrice reala

Daca operatorul real 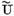este compact atunci evident si operatorul U indus de el din 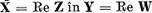este de asemenea compact. Este valabila si afirmatia reciproca : daca U este operatorul compact din X in Y atunci extensia lui complexa, operatorul 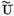, este compacta.

Pentru a demonstra acest fapt este suficient sa observam ca din convergenta sirului 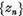rezulta convergenta sirurilor 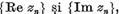si reciproc.

3.Nucleul real al spatiului dual

.Daca spatiul Z are o structura reala atunci si spatiul dual 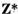are o structura reala.

Intradevar fie 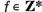; definim involutia 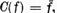prin

Vom stabili intai ca f este o functionala liniara continua. Pentru aceasta

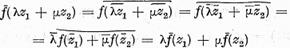
si

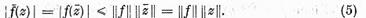
Tinand seama de regula de inmultire a unei functionale cu un numar complex avem

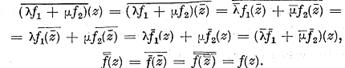
In sfarsit din integralitatea (5) rezulta ca 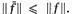Pe de alta parte

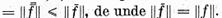
Sa notam X nucleul real al spatiului Z si sa demonstram ca daca 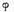este o functionala liniara pe spatiul real X atunci extensia complexa f a functionalei 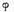apartine nucleului real al spatiului si ca aceasta se compune numai din functionalele de aceasta forma. Ambele afirmatii rezulta fara dificultate din definitia conjugatei unei functionale . Intradevar daca f este extensia complexa a functionalei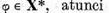

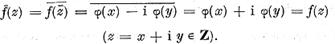
Reciproc daca functionala f este un element real al spatiului 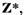adica daca 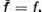atunci . In particular , daca z =

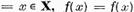, adica f(x) este real

Afirmatia demonstrata poate fi enuntata astfel : nucleul real al spatiului dual este spatiul dual al nucleului real al spatiului dat.

Este natural sa ne asteptam ca adjunctul unui operator real sa fie la randul lui un operator real. Fie 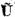un operator real care aplica spatiului Z in spatiul W si U operatorul din spatiul X in Y indus de acesta 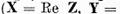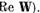Sa demosntram ca este operatorul real si ca operatorul de la spatiul 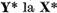indus de el este 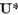. Ultima afirmatie trebuie inteleasa in sensul urmator : daca 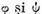sunt functionale pe spatiile X si Y astfel incat

atunci

unde f este extensia complexa a functionalei iar g este extensia complexa a functionalei , reciproc daca functionalele reale sunt legate prin relatia (7) atunci functionalele 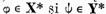induse de ele sunt legate prin relatia (6).

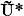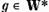Faptul ca operatorul este real se demonstreaza foarte simplu : daca este o functionala reala, adica 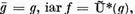atunci

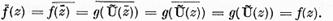
Fie mai departe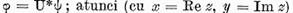

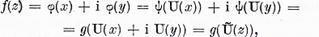
astfel incat 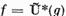. Tot asa de simplu se stabileste ca din relatia (7) rezulta relatia (6)