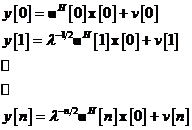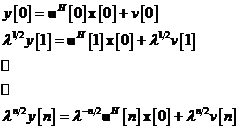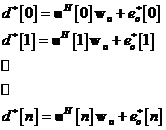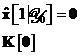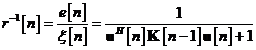Filtrul Kalman
Acest capitol
completeaza studiul filtrelor optimale lineare prin trecerea in revista a
fundamentelor filtrarii Kalman. O caracteristica deosebita a unui filtru
Kalman este faptul ca pentru descrierea sa matematica se utilizeaza conceptul
de spatiu al starilor. O alta trasatura care deosebeste filtrul Kalman de
filtrul optimal linear este faptul ca solutia sa se calculeaza recursiv.
In particular, fiecare noua estimare a starii se calculeaza pe baza estimarii
anterioare si a noii valori a marimii de intrare, astfel incat numai ultima
estimare trebuie memorata. Aceasta caracteristica reduce volumul de calcul
necesar implementarii filtrului Kalman pe un calculator electronic. In
consecinta, filtrele Kalman au fost implementate cu succes in multe aplicatii
practice, in particular in industria aeronautica si spatiala.
Atentia pe care o
acordam filtrelor Kalman se justifica prin aceea ca ele ofera un cadru unitar
pentru fundamentarea matematica a filtrelor adaptive ce se bazeaza pe calcul
recursiv. In ceea ce priveste reprezentarea prin spatiul starilor, pe langa
numeroase aspecte favorabile care vor fi evidentiate in continuare, aceasta se
bucura de avantajele utilizarii metodelor algebrei lineare ceea ce permite
punerea in evidenta a unor proprietati remarcabile.
Se considera un
sistem dinamic linear in timp discret descris de graful de semnal din Fig. 11. . Reprezentarea sistemului in domeniul timp utilizata
aici ofera urmatoarele avantaje:
este convenabila din punct de vedere matematic si al notatiilor
utilizate
are o puternica legatura cu realitatea fizica
constituie o baza utila pentru evidentierea comportarii statistice a
sistemului
Notiunea de stare
joaca un rol esential in aceasta reprezentare. Vectorul de stare de
dimensiune 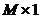 desemnat prin
desemnat prin 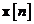 in Fig. 11. se defineste ca orice ansamblu de marimi suficiente
pentru a descrie comportarea dinamica nefortata a sistemului la momente de timp
in Fig. 11. se defineste ca orice ansamblu de marimi suficiente
pentru a descrie comportarea dinamica nefortata a sistemului la momente de timp
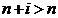 . Cu alte cuvinte, starea unui sistem reprezinta un rezumat de
informatii suficiente ce permit descrierea evolutiei sistemului. Vectorul de
stare
. Cu alte cuvinte, starea unui sistem reprezinta un rezumat de
informatii suficiente ce permit descrierea evolutiei sistemului. Vectorul de
stare 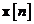 nu este in mod necesar direct
accesibil pentru a fi masurat, astfel incat pentru a fi evaluat se utilizeaza
un set de date observabile, descrise in Fig.
11. prin vectorul
nu este in mod necesar direct
accesibil pentru a fi masurat, astfel incat pentru a fi evaluat se utilizeaza
un set de date observabile, descrise in Fig.
11. prin vectorul 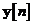 de dimensiune
de dimensiune 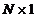
In termeni
matematici, graful de semnal din Fig.
11. incorporeaza urmatoarea pereche de ecuatii:
Fig. 11. Reprezentarea prin graf de semnal a unui sistem in timp discret linear
si dinamic
|
O
ecuatie de proces
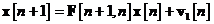
unde 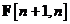 este o matrice de tranzitie a starilor de dimensiune
este o matrice de tranzitie a starilor de dimensiune 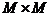 ce este cunoscuta si care
exprima legatura dintre starile sistemului la momentele
ce este cunoscuta si care
exprima legatura dintre starile sistemului la momentele 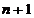 si
si 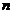 . Vectorul de dimensiune
. Vectorul de dimensiune 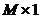
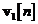 reprezinta semnalul de intrare a
procesului. De obicei, in cazul abordarii statistice a modelarii sistemului, el
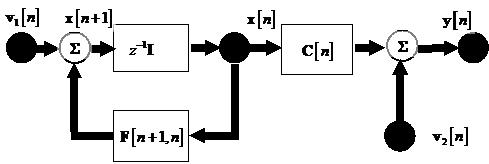
este zgomotul de proces, un proces de zgomot alb cu media nula, si are
matricea de corelatie
reprezinta semnalul de intrare a
procesului. De obicei, in cazul abordarii statistice a modelarii sistemului, el
este zgomotul de proces, un proces de zgomot alb cu media nula, si are
matricea de corelatie
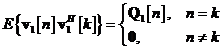
O ecuatie de masurare, ce
stabileste vectorul de observatie prin relatia:
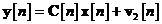
unde 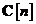 este o matrice de masurare
de dimensiune
este o matrice de masurare
de dimensiune 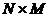 cunoscuta. Vectorul de dimensiune
cunoscuta. Vectorul de dimensiune 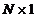
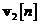 este denumit zgomot de
masurare. Este, de obicei, modelat printr‑un proces de zgomot alb ce
are matricea de corelatie
este denumit zgomot de
masurare. Este, de obicei, modelat printr‑un proces de zgomot alb ce
are matricea de corelatie
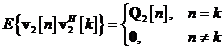
Se presupune
ca valoarea starii initiale, 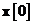 , este necorelata atat cu
, este necorelata atat cu 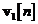 cat si cu
cat si cu 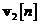 pentru
pentru 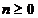 . Vectorii de zgomot
. Vectorii de zgomot 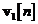 si
si 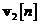 sunt statistic independenti,
astfel ca se poate scrie
sunt statistic independenti,
astfel ca se poate scrie
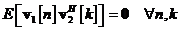
Problema filtrarii
Kalman poate fi acum formulata dupa cum urmeaza: Sa se utilizeze toate datele
observate, ce constau din vectorii 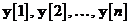 , pentru a stabili pentru fiecare
, pentru a stabili pentru fiecare 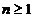 estimarea de medie patratica
minima a componentelor starii
estimarea de medie patratica
minima a componentelor starii 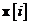 . Ea este denumita problema de filtrare daca
. Ea este denumita problema de filtrare daca 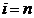 , problema de predictie daca
, problema de predictie daca 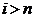 si, in sfarsit,
problema de mediere daca
si, in sfarsit,
problema de mediere daca 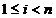 . In continuare ne vom concentra asupra problemelor de filtrare si
predictie care sunt strans legate, facand apel la o abordare bazata pe procesul
de inovatii.
. In continuare ne vom concentra asupra problemelor de filtrare si
predictie care sunt strans legate, facand apel la o abordare bazata pe procesul
de inovatii.
Desemnam prin
vectorul 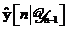 estimarea de medie patratica
minima a datelor observate
estimarea de medie patratica
minima a datelor observate 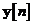 la momentul
la momentul 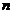 . Estimarea se face pe baza tuturor valorilor anterioare ale datelor de
observatie, incepand cu momentul
. Estimarea se face pe baza tuturor valorilor anterioare ale datelor de
observatie, incepand cu momentul 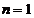 si pana la, inclusiv momentul
si pana la, inclusiv momentul 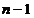 . Aceste valori anterioare sunt reprezentate prin vectorii
. Aceste valori anterioare sunt reprezentate prin vectorii 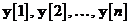 , care subintind spatiul vectorial
, care subintind spatiul vectorial 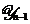 . Se defineste procesul de inovatii asociat vectorului de
observatie
. Se defineste procesul de inovatii asociat vectorului de
observatie 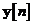 prin:
prin:
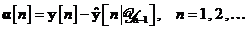
Vectorul 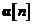 de dimensiune
de dimensiune 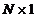 rerezinta informatia noua in
datele observate
rerezinta informatia noua in
datele observate 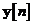
Pe baza
caracteristicilor generale ale semnalului de eroare in cazul filtrului optimal,
se demonstreaza ca procesul de inovatii are urmatoarele proprietati:
Procesul de inovatii 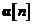 asociat vectorului de date
observate
asociat vectorului de date
observate 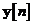 la momentul
la momentul 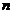 , este ortogonal pe toate observatiile anterioare, dupa cum evidentiaza
ecuatia de mai jos:
, este ortogonal pe toate observatiile anterioare, dupa cum evidentiaza
ecuatia de mai jos:
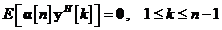
Procesul de inovatii consta
dintr-o secventa de vectori variabile aleatoare, ortogonali unul pe celalalt,
fapt evidentiat prin:
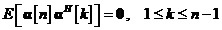
Exista o corespondenta
biunivoca intre secventa de vectori variabile aleatoare ce reprezinta datele
observate, 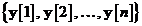 si secventa de vectori variabile
aleatoare
si secventa de vectori variabile
aleatoare 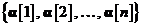 care reprezinta procesul de
inovatii, in sensul ca o secventa poate fi obtinuta din cealalta prin
intermediul unor operatori lineari stabili fara pierdere de informatie. Aceasta
ultima afirmatie este descrisa matematic prin:
care reprezinta procesul de
inovatii, in sensul ca o secventa poate fi obtinuta din cealalta prin
intermediul unor operatori lineari stabili fara pierdere de informatie. Aceasta
ultima afirmatie este descrisa matematic prin:
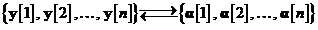
Pentru a forma secventa de vectori variabile
aleatoare ce defineste procesul de inovatii, se pot utiliza tehnici specifice
calculului matricial, de exemplu procedura de ortogonalizare Gram-Schmidt.
Matricea de
autocorelatie a procesului de inovatii
Pentru a determina
matricea de corelatie a procesului de inovatii 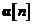 , se incepe prin a rezolva recursiv ecuatia de stare , ceea ce conduce
la relatia
, se incepe prin a rezolva recursiv ecuatia de stare , ceea ce conduce
la relatia
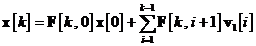
In relatia s-au utilizat urmatoarele presupuneri si proprietati:
Valoarea initiala a
vectorului de stare este 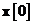
Se presupune ca datele
observate, si prin urmare vectorul de zgomot de stare 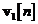 sunt nule pentru
sunt nule pentru 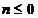
Matricea de tranzitie a
starilor are proprietatile
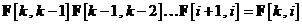
si
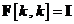
unde 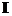 este matricea identitate. De
observat ca pentru un sistem invariant in timp se scrie
este matricea identitate. De
observat ca pentru un sistem invariant in timp se scrie
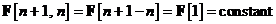
Ecuatia arata faptul ca 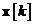 este o combinatie lineara de
este o combinatie lineara de 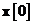 si
si 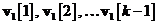
Prin ipoteza,
vectorul zgomotului de masurare 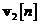 este necorelat atat cu vectorul
de stare initial
este necorelat atat cu vectorul
de stare initial 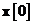 cat si cu vectorul de zgomot a
procesului
cat si cu vectorul de zgomot a
procesului 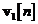 . In consecinta, multiplicand ambii termeni ai ecuatiei cu
. In consecinta, multiplicand ambii termeni ai ecuatiei cu 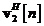 si mediind statistic, se deduce
ca:
si mediind statistic, se deduce
ca:
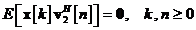
Corespunzator, din ecuatia de masurare se poate deduce:
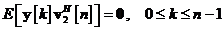
Mai mult, se poate scrie
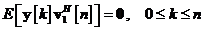
Fiind date observatiile
anterioare 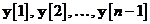 ce definesc spatiul vectorial
ce definesc spatiul vectorial 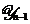 , putem de asemenea evidentia din ecuatia de masurare , faptul ca estimarea de medie patratica minima a valorii curente a
vectorului de observare
, putem de asemenea evidentia din ecuatia de masurare , faptul ca estimarea de medie patratica minima a valorii curente a
vectorului de observare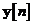 este data de:
este data de:
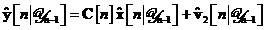
Totusi, estimarea 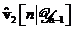 a vectorului de zgomot de
masurare este nula, intrucat
a vectorului de zgomot de
masurare este nula, intrucat 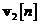 este ortogonala pe observatiile
anterioare
este ortogonala pe observatiile
anterioare 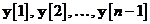 ; vezi ecuatia . Prin urmare, se scrie pur si simplu
; vezi ecuatia . Prin urmare, se scrie pur si simplu
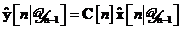
Prin urmare, utilizand ecuatiile si , putem exprima procesul de inovatii sub forma
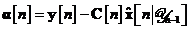
Inlocuind ecuatia de masurare in , se obtine:
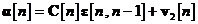
unde 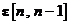 este vectorul de eroare a
predictiei de stare la momentul
este vectorul de eroare a
predictiei de stare la momentul 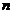 , pe baza datelor disponibile pana la momentul
, pe baza datelor disponibile pana la momentul 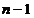 . Prin urmare,
. Prin urmare, 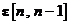 este diferenta dintre vectorul
de stare si vectorul de predictie inainte cu un pas
este diferenta dintre vectorul
de stare si vectorul de predictie inainte cu un pas 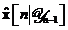
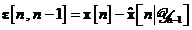
Se observa ca vectorul de predictie a erorii de stare este ortogonal
atat pe vectorul de zgomot de proces 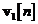 cat si pe vectorul de zgomot de
masurare
cat si pe vectorul de zgomot de
masurare 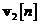
Matricea de
autocorelatie a procesului de inovatii 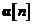 se defineste prin
se defineste prin
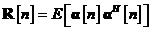
Inlocuim in continuare ecuatia in , dezvoltam expresia obtinuta, si avand in vedere faptul ca vectorii 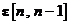 si
si 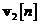 sunt ortogonali se obtine
rezultatul:
sunt ortogonali se obtine
rezultatul:
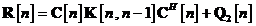
unde 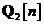 este matricea de autocorelatie a
vectorului de zgomot
este matricea de autocorelatie a
vectorului de zgomot 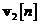 . Matricea de dimensiune
. Matricea de dimensiune 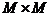
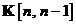 poarta numele de matricea de
autocorelatie a erorii de predictie a starii, fiind definita prin
poarta numele de matricea de
autocorelatie a erorii de predictie a starii, fiind definita prin
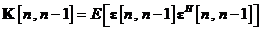
unde 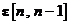 este vectorul de eroare a
predictiei de stare. Matricea
este vectorul de eroare a
predictiei de stare. Matricea 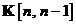 se foloseste pentru descrierea
statistica a erorii facute prin utilizarea estimarii
se foloseste pentru descrierea
statistica a erorii facute prin utilizarea estimarii 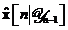
Vom lua in
considerare in continuare problema determinarii estimarii de medie patratica
minima a starii 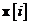 pe baza procesului de inovatii.
Se poate demonstra faptul ca aceasta estimare poate fi exprimata ca o
combinatie lineara a secventei de procese de inovatii
pe baza procesului de inovatii.
Se poate demonstra faptul ca aceasta estimare poate fi exprimata ca o
combinatie lineara a secventei de procese de inovatii 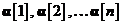
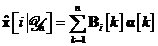
unde 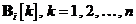 , este un set de matrici
, este un set de matrici 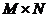 ce urmeaza a fi determinate. In
conformitate cu principiul ortogonalitatii, vectorul de eroare a predictiei de
stare este ortogonal pe procesul de inovatii, asa cum exprima ecuatia care
urmeaza
ce urmeaza a fi determinate. In
conformitate cu principiul ortogonalitatii, vectorul de eroare a predictiei de
stare este ortogonal pe procesul de inovatii, asa cum exprima ecuatia care
urmeaza
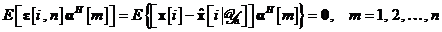
Inlocuind
ecuatia in si apeland la principiul ortogonalitatii pentru procesul de inovatii,
in particular la ecuatia , se obtine
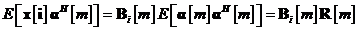
In
consecinta, inmultind la dreapta ambii membri ai ecuatiei cu matricea inversa 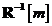 . gasim pentru matricea
. gasim pentru matricea 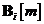 expresia
expresia
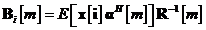
In
final, prin inlocuirea ecuatiei in se obtine estimata de medie patratica minima
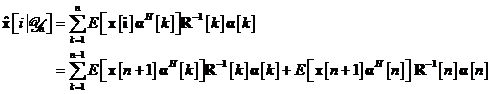
Vom
particulariza relatia pentru 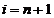
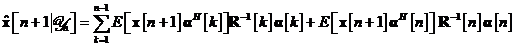
In
ceea ce priveste starea 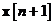 de la momentul
de la momentul 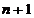 , ea este legata de starea
, ea este legata de starea 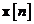 de la momentul
de la momentul 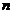 prin ecuatia de proces . Drept urmare, utilizand aceasta relatie, putem scrie pentru
prin ecuatia de proces . Drept urmare, utilizand aceasta relatie, putem scrie pentru 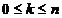
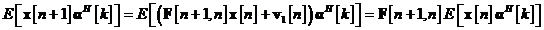
In
ultima relatie s-a folosit faptul ca 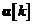 depinde numai de datele observate
depinde numai de datele observate 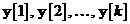 , si prin urmare din ecuatia se observa ca
, si prin urmare din ecuatia se observa ca 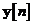 si
si 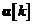 sunt ortogonali pentru
sunt ortogonali pentru 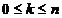 . Putem atunci rescrie suma din membrul drept al ecuatiei dupa cum urmeaza:
. Putem atunci rescrie suma din membrul drept al ecuatiei dupa cum urmeaza:
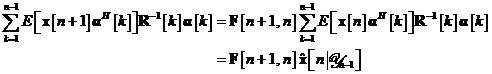
Vom
introduce in continuare cateva definitii fundamentale, necesare pentru
formularea problemei filtrarii Kalman.
Matricea de
castig Kalman
Se introduce
matricea 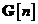 de dimensiuni
de dimensiuni 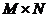 , definita prin:
, definita prin:
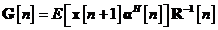
Utilizam in continuare aceasta definitie si
rezultatul ecuatiei , pentru a rescrie ecuatia dupa cum urmeaza:
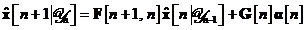
Ecuatia are o importanta fundamentala, reprezentand formula de calcul recursiv
utilizata in cazul filtrului adaptiv Kalman. Ea evidentiaza faptul ca estimarea
de medie patratica minima 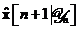 a starii unui sistem dinamic
linear, poate fi calculata prin adaugarea la estimarea starii anterioare a
sistemului
a starii unui sistem dinamic
linear, poate fi calculata prin adaugarea la estimarea starii anterioare a
sistemului 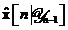 multiplicata cu matricea de
tranzitie a starii
multiplicata cu matricea de
tranzitie a starii 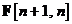 , a unui termen de corectie egal cu
, a unui termen de corectie egal cu 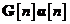 . Termenul de corectie este egal cu vectorul procesului de inovatii
. Termenul de corectie este egal cu vectorul procesului de inovatii 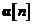 multiplicat inainte cu matricea
multiplicat inainte cu matricea 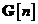 . Drept urmare, si in semn de recunoastere a meritelor de pionierat ale
lui Kalman, matricea
. Drept urmare, si in semn de recunoastere a meritelor de pionierat ale
lui Kalman, matricea 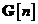 este numita matricea de castig a
lui Kalman.
este numita matricea de castig a
lui Kalman.
Ramane problema
exprimarii matricii de castig a lui Kalman 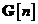 intr-o forma convenabila
calculului. Pentru a ajunge la rezultat, vom face apel la ecuatiile si pentru a exprima media produsului lui
intr-o forma convenabila
calculului. Pentru a ajunge la rezultat, vom face apel la ecuatiile si pentru a exprima media produsului lui 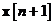 cu
cu 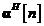 dupa cum urmeaza:
dupa cum urmeaza:
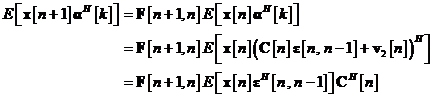
unde s-a utilizat constatarea ca starea 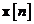 si vectorul de zgomot
si vectorul de zgomot 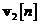 sunt necorelate (vezi ecuatia . Mai mult, in conformitate cu principiul ortogonalitatii, sa notam ca
vectorul de predictie a erorii de stare
sunt necorelate (vezi ecuatia . Mai mult, in conformitate cu principiul ortogonalitatii, sa notam ca
vectorul de predictie a erorii de stare 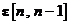 este ortogonal pe estimarea
este ortogonal pe estimarea 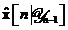 . Prin urmare, media statistica a produsului
. Prin urmare, media statistica a produsului 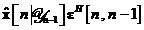 este nula, astfel incat putem
rescrie ecuatia , inlocuind factorul multiplicativ
este nula, astfel incat putem
rescrie ecuatia , inlocuind factorul multiplicativ 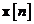 prin vectorul de predictie a
erorii de stare
prin vectorul de predictie a
erorii de stare 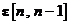 , ca mai jos:
, ca mai jos:
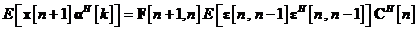
Facem apel in continuare la ecuatia pentru a evidentia faptul ca media statistica din membrul drept al
ecuatiei este egal cu matricea de autocorelatie a erorii de predictie a starii.
Drept urmare, ecuatia este rescrisa astfel:
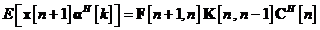
Acum, poate fi redefinita matricea de castig a
lui Kalman. In particular, inlocuim relatia in pentru a obtine
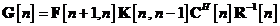
unde matricea de autocorelatie 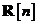 este ea insasi definita prin
ecuatia
este ea insasi definita prin
ecuatia

Fig. 11. Diagrama de calcul
a matricii de castig Kalman
|
Schema bloc din Fig. 11. ilustreaza graful de semnal al ecuatiei pentru calculul matricii de castig Kalman 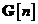 . Odata calculata matricea de castig Kalman
. Odata calculata matricea de castig Kalman 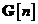 , se poate utiliza ecuatia pentru a reinnoi cu un nou pas predictia. Cu alte cuvinte, fiind data
vechea predictie
, se poate utiliza ecuatia pentru a reinnoi cu un nou pas predictia. Cu alte cuvinte, fiind data
vechea predictie 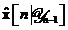 , se calculeaza predictia curenta
, se calculeaza predictia curenta 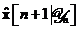 , proces ilustrat prin graful de semnal din Fig. 11. . In aceasta din urma figura, s-a utilizat de asemenea
ecuatia pentru determinarea vectorului procesului de inovatii
, proces ilustrat prin graful de semnal din Fig. 11. . In aceasta din urma figura, s-a utilizat de asemenea
ecuatia pentru determinarea vectorului procesului de inovatii 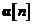
|
Fig. 11. Predictorul Kalman inainte
intr-un pas
|
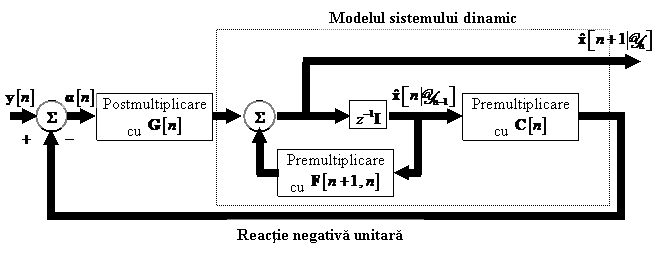
Ecuatia Riccati
Ecuatia de calcul
a matricii de castig Kalman nu este utila sub forma actuala, intrucat pentru determinarea lui 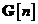 este nevoie de cunoasterea
valorii matricii de autocorelatie a erorii de predictie a starii
este nevoie de cunoasterea
valorii matricii de autocorelatie a erorii de predictie a starii 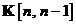 . Pentru a depasi aceasta dificultate, vom deduce in continuare o
formula de calcul recursiv pentru matricea
. Pentru a depasi aceasta dificultate, vom deduce in continuare o
formula de calcul recursiv pentru matricea 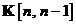
Vectorul de eroare
a predictiei de stare 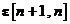 este egal cu diferenta dintre
vectorul de stare
este egal cu diferenta dintre
vectorul de stare 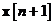 si predictia inainte intr-un pas
a acestuia
si predictia inainte intr-un pas
a acestuia 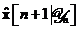 (vezi ecuatia
(vezi ecuatia
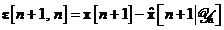
Inlocuind ecuatiile si in , si utilizand ecuatia pentru vectorul procesului de inovatii 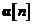 , obtinem:
, obtinem:
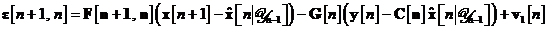
In continuare, se utilizeaza ecuatia pentru a elimina vectorul 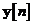 din ecuatia . Se obtine ecuatia cu diferente finite de mai jos, care se utilizeaza
la calculul recursiv al vectorului de predictie al erorii de stare:
din ecuatia . Se obtine ecuatia cu diferente finite de mai jos, care se utilizeaza
la calculul recursiv al vectorului de predictie al erorii de stare:
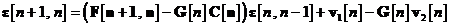
Matricea de autocorelatie a vectorului de
predictie a erorii de stare 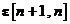 este data in conformitate cu
ecuatia de relatia:
este data in conformitate cu
ecuatia de relatia:
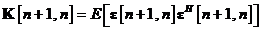
Inlocuind ecuatia in , si acceptand ipoteza ca vectorul de eroare 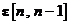 si vectorii de zgomot
si vectorii de zgomot 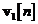 si
si 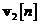 sunt mutual necorelati, putem
exprima matricea de autocorelatie a vectorului de predictie a erorii de stare
dupa cum urmeaza:
sunt mutual necorelati, putem
exprima matricea de autocorelatie a vectorului de predictie a erorii de stare
dupa cum urmeaza:
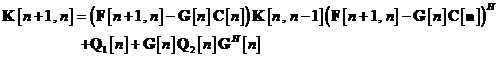
unde 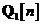 si
si 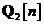 sunt matricile de autocorelatie
ale lui
sunt matricile de autocorelatie
ale lui 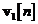 respectiv
respectiv 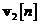 . Dezvoltam, in continuare, membrul drept al ecuatiei si apoi utilizam ecuatiile si pentru matricea de castig Kalman. Se obtine ecuatia cu diferente
finite Riccati ce permite calculul recursiv al matricii de autocorelatie al
predictiei erorii de stare:
. Dezvoltam, in continuare, membrul drept al ecuatiei si apoi utilizam ecuatiile si pentru matricea de castig Kalman. Se obtine ecuatia cu diferente
finite Riccati ce permite calculul recursiv al matricii de autocorelatie al
predictiei erorii de stare:
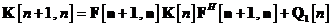
unde matricea patrata de dimensiuni 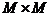
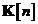 este definita prin ecuatia de
recursie:
este definita prin ecuatia de
recursie:
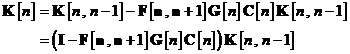
S-a utilizat aici proprietatea:
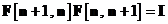
unde 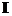 este matricea identitate. Aceasta
proprietate este o consecinta a definitiei matricii de tranzitie. Semnificatia
matematica a matricii
este matricea identitate. Aceasta
proprietate este o consecinta a definitiei matricii de tranzitie. Semnificatia
matematica a matricii 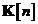 din ecuatia va fi lamurita in paragraful urmator.
din ecuatia va fi lamurita in paragraful urmator.
Fig. 11. este reprezentarea prin graf de semnal al ecuatiilor si , reprezentare facuta chiar in aceasta ordine. Acest graf poate fi
vazut ca o reprezentare al calculatorului ecuatiei Riccati, prin aceea
ca fiind data vechea valoare 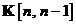 , el calculeaza valoarea curenta
, el calculeaza valoarea curenta 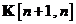
Ecuatiile si , in ordinea enuntata, definesc algoritmul de predictie inainte a lui
Kalman intr-un pas.

Fig. 11. Graful de semnal al rezolvarii ecuatiei Riccati (Calculatorul
ecuatiei Riccati)
|
Comentarii
Procesul aplicat la intrarea
filtrului Kalman consta din datele observate 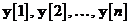 care definesc spatiul vectorial
care definesc spatiul vectorial 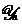 .
Iesirea care rezulta a filtrului este egala cu vectorul de predictie a starii
.
Iesirea care rezulta a filtrului este egala cu vectorul de predictie a starii 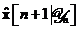 . Fiind cunoscute matricile
. Fiind cunoscute matricile 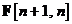 ,
,
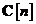 ,
,
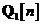 si
si 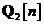 ,
se stabileste din ecuatiile si faptul ca matricea de corelatie a
predictiei erorii de stare
,
se stabileste din ecuatiile si faptul ca matricea de corelatie a
predictiei erorii de stare 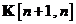 este independenta de marimea de intrare a
filtrului
este independenta de marimea de intrare a
filtrului 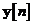 ,
oricare ar fi aceasta. Matricea de castig Kalman
,
oricare ar fi aceasta. Matricea de castig Kalman 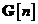 este de asemenea independenta de
este de asemenea independenta de 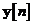 .
in consecinta, matricea de corelatie a predictiei erorii de stare
.
in consecinta, matricea de corelatie a predictiei erorii de stare 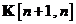 si matricea de castig a lui Kalman
si matricea de castig a lui Kalman 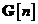 pot fi calculate inainte ca filtrul Kalman sa
intre propriuzis in operare. Utilizand matricea de corelatie
pot fi calculate inainte ca filtrul Kalman sa
intre propriuzis in operare. Utilizand matricea de corelatie 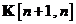 pentru a furniza o descriere statistica a
erorii vectorului de predictie a starii
pentru a furniza o descriere statistica a
erorii vectorului de predictie a starii 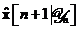 ,
aceasta poate fi examinata pe baza filtrului Kalman care produce o realizare a
unui sistem fizic care prezinta interes. In acest fel, se poate stabili daca
gradul de satisfactie oferit de solutia furnizata de filtrul Kalman este convenabil.
,
aceasta poate fi examinata pe baza filtrului Kalman care produce o realizare a
unui sistem fizic care prezinta interes. In acest fel, se poate stabili daca
gradul de satisfactie oferit de solutia furnizata de filtrul Kalman este convenabil.
Vom considera, in
continuare, operatia de filtrare. In particular, dorim sa calculam estimarea
filtrata 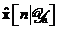 pornind de la algoritmul de predictie intr-un
pas descris anterior.
pornind de la algoritmul de predictie intr-un
pas descris anterior.
Sa notam, pentru inceput faptul ca vectorul de stare 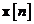 si vectorul de zgomot
si vectorul de zgomot 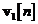 sunt independenti unul fata de celalalt. Prin
urmare, stabilim din ecuatia de stare ca estimarea de eroare medie
patratica minima a starii
sunt independenti unul fata de celalalt. Prin
urmare, stabilim din ecuatia de stare ca estimarea de eroare medie
patratica minima a starii 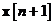 la momentul
la momentul 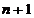 ,
fiind date observatiile facute pana la inclusiv momentul
,
fiind date observatiile facute pana la inclusiv momentul 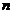 (adica
(adica 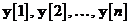 ) este
) este
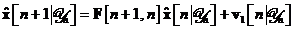
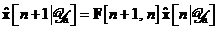
Pentru a stabili
estimarea filtrata 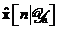 , multiplicam inainte ambii termeni
ai ecuatiei cu inversa matricii de tranzitie
, multiplicam inainte ambii termeni
ai ecuatiei cu inversa matricii de tranzitie 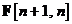 :
:
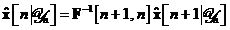
Utilizand
proprietatea matricii de tranzitie a starilor, data in , putem scrie
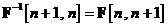
si sa reluam ecuatia in forma echivalenta:
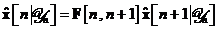
Ultima relatie arata ca pornind de la
solutia problemei predictiei intr-un pas, care este estimarea de medie
patratica minima 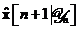 , putem determina estimarea filtrata
corespunzatoare
, putem determina estimarea filtrata
corespunzatoare 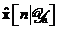 prin multiplicarea lui
prin multiplicarea lui 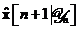 cu matricea de tranzitie a starilor
cu matricea de tranzitie a starilor 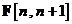 .
.
Eroarea de
estimare filtrata si factorul de conversie
In contextul discutarii operatiunii de
filtrare, este normala introducerea unui vector de eroare a estimarii
filtrate a starii sistemului. El se defineste astfel:
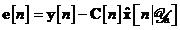
Aceasta definitie este similara definitiei vectorului de inovatii 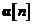 din , cu exceptia faptului ca estimarea filtrata
din , cu exceptia faptului ca estimarea filtrata 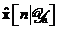 a inlocuit estimarea prezisa
a inlocuit estimarea prezisa 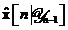 .
Inlocuind relatiile si in , se obtine
.
Inlocuind relatiile si in , se obtine
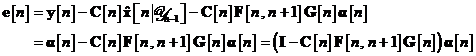
Marimea matriciala din interiorul
parantezei rotunde a ecuatiei este numita factor de conversie, furnizand o formula pentru
conversia vectorului de inovatii 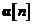 in vectorul de eroare a estimarii filtrate
in vectorul de eroare a estimarii filtrate 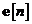 .
Facem apel la ecuatia pentru a elimina matricea de castig Kalman
.
Facem apel la ecuatia pentru a elimina matricea de castig Kalman 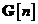 din aceasta definitie, si eliminand termenii
comuni, putem rescrie relatia in forma echivalenta:
din aceasta definitie, si eliminand termenii
comuni, putem rescrie relatia in forma echivalenta:
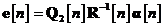
unde 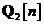 este matricea de autocorelatie a procesului de
zgomot de masurare
este matricea de autocorelatie a procesului de
zgomot de masurare 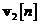 ,
iar matricea
,
iar matricea 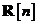 se defineste prin relatia ca matricea de autocorelatie a procesului de inovatii
se defineste prin relatia ca matricea de autocorelatie a procesului de inovatii 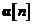 .
Astfel, cu exceptia unei premultiplicari cu matricea
.
Astfel, cu exceptia unei premultiplicari cu matricea 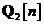 ,
relatia arata ca matricea inversa
,
relatia arata ca matricea inversa 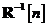 joaca rolul unui factor de conversie in teoria
filtrarii Kalman. Intr-adevar, in cazul special in care
joaca rolul unui factor de conversie in teoria
filtrarii Kalman. Intr-adevar, in cazul special in care 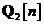 este egala cu matricea unitate, matricea
inversa
este egala cu matricea unitate, matricea
inversa 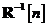 reprezinta exact factorul de conversie definit
mai sus.
reprezinta exact factorul de conversie definit
mai sus.
Matricea de
corelatie a erorii de stare filtrata
S-a introdus anterior la formularea
ecuatiei cu diferente Riccati , matricea de dimensiuni 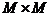
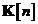 .
Vom concluziona aceasta discutie asupra teoriei filtrului Kalman prin
demonstrarea faptului ca aceasta matrice este egala cu matricea de
autocorelatie a erorii ce se face la estimarea starii filtrate
.
Vom concluziona aceasta discutie asupra teoriei filtrului Kalman prin
demonstrarea faptului ca aceasta matrice este egala cu matricea de
autocorelatie a erorii ce se face la estimarea starii filtrate 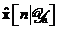
Se defineste vectorul de eroare a
starii filtrate 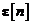 ca diferenta dintre starea
ca diferenta dintre starea 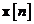 si estimarea filtrata a acesteia
si estimarea filtrata a acesteia 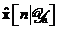
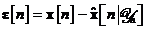
Inlocuind ecuatiile si in , si recunoscand faptul ca produsul 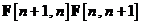 este egal cu matricea unitate, se obtine
este egal cu matricea unitate, se obtine
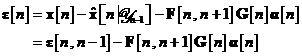
unde 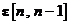 este vectorul de eroare a predictiei de stare
la momentul de timp
este vectorul de eroare a predictiei de stare
la momentul de timp 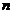 pe baza datelor existente pana la momentul
pe baza datelor existente pana la momentul 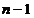 iar
iar 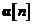 este
vectorul procesului de inovatii.
este
vectorul procesului de inovatii.
Prin definitie, matricea de autocorelatie
a vectorului de eroare a starii filtrate 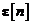 este egala cu media statistica
este egala cu media statistica 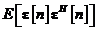 .
In consecinta, utilizand ecuatia , se poate exprima aceasta medie dupa cum urmeaza:
.
In consecinta, utilizand ecuatia , se poate exprima aceasta medie dupa cum urmeaza:
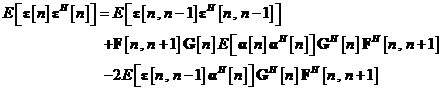
In urma examinarii membrului drept ale
ccuatiei se poate stabili faptul ca cele trei medii statistice din componenta
sa pot fi interpretate individual dupa cum urmeaza:
Prima medie este egala cu matricea
de autocorelatie a erorii de predictie a starii:
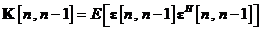
Media statistica din cel de al
doilea termen este egala cu matricea de autocorelatie a procesului de inovatii 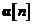 :
:
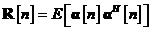
Media din cel de-al treilea termen
poate fi exprimata dupa cum urmeaza:
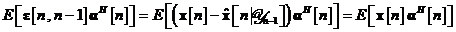
unde, ultima
expresie s-a obtinut in urma observatiei ca estimarea 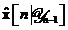 este ortogonala pe procesul de
observatii
este ortogonala pe procesul de
observatii 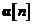 ,
ce reprezinta intrarea filtrului Kalman. In continuare din ecuatia se observa ca, punand
,
ce reprezinta intrarea filtrului Kalman. In continuare din ecuatia se observa ca, punand 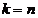 si apoi multiplicand inainte ambii membri ai
relatiei prin matricea inversa
si apoi multiplicand inainte ambii membri ai
relatiei prin matricea inversa 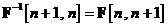 se obtine
se obtine
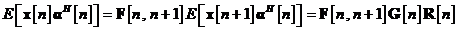
unde in ultima
relatie s-a facut apel la ecuatia . Prin urmare
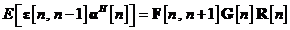
In continuare, putem utiliza aceste
relatii in ecuatia pentru a obtine
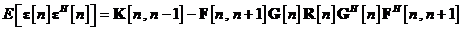
Ultima relatie poate fi simplificata in
continuare observand din ecuatia ca:
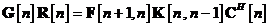
Drept urmare, utilizand relatiile si si avand in vedere faptul ca produsul 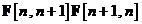 este egal cu matricea unitate, obtinem
rezultatul dorit pentru matricea de autocorelatie a erorii de stare filtrate
este egal cu matricea unitate, obtinem
rezultatul dorit pentru matricea de autocorelatie a erorii de stare filtrate
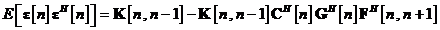
Echivalent, prin utilizarea proprietatii de a
fi hermitica pentru 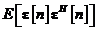 si
si 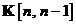 ,
putem scrie:
,
putem scrie:
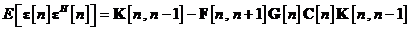
Comparam relatia cu pentru a evidentia ca
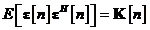
Aceasta demonstreaza ca matricea 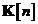 utilizata in ecuatia Riccati cu diferente
finite este de fapt matricea de autocorelatie a erorii de stare filtrate.
Matricea
utilizata in ecuatia Riccati cu diferente
finite este de fapt matricea de autocorelatie a erorii de stare filtrate.
Matricea 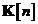 este folosita la descrierea statistica a
erorii estimarii filtrate
este folosita la descrierea statistica a
erorii estimarii filtrate 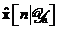
Pentru a pune in miscare algoritmii de
predictie intr-un pas si de filtrare descrisi in paragrafele 11.3 si , este obligatorie specificarea conditiilor
initiale. Vom prezenta in continuare modalitatea de rezolvare a acestei
probleme.
Starea initiala a procesului descris prin
ecuatia nu se cunoaste cu precizie. Ea se descrie de obicei prin media si
matricea sa de autocorelatie. In absenta oricarei date observate la momentul 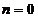 ,
putem alege drept estimare de predictie initiala valoarea:
,
putem alege drept estimare de predictie initiala valoarea:
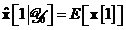
iar drept matrice de autocorelatie
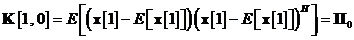
Aceasta modalitate de selectare a conditiilor
initiale nu numai ca satisface intuitiv dar are de asemenea avantajul de a
furniza o estimare filtrata a starii 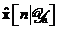 care este nedeplasata.
Presupunand ca vectorul de stare
care este nedeplasata.
Presupunand ca vectorul de stare 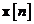 este de medie nula, putem simplifica
relatiile si impunand
este de medie nula, putem simplifica
relatiile si impunand
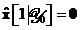
si
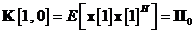
Tabela
11. prezinta un rezumat al variabilelor utilizate la
formularea solutiei problemei de filtrare Kalman. Intrarea filtrului este
vectorul de proces 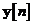 ,
reprezentat prin spatiul vectorial
,
reprezentat prin spatiul vectorial 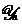 ,
iar iesirea este estimarea filtrata
,
iar iesirea este estimarea filtrata 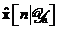 a vectorului de stare. Tabela 11. prezinta un rezumat al
filtrului Kalman (inclusiv conditiile initiale) ce este bazat pe algoritmul de
predictie intr-un pas.
a vectorului de stare. Tabela 11. prezinta un rezumat al
filtrului Kalman (inclusiv conditiile initiale) ce este bazat pe algoritmul de
predictie intr-un pas.
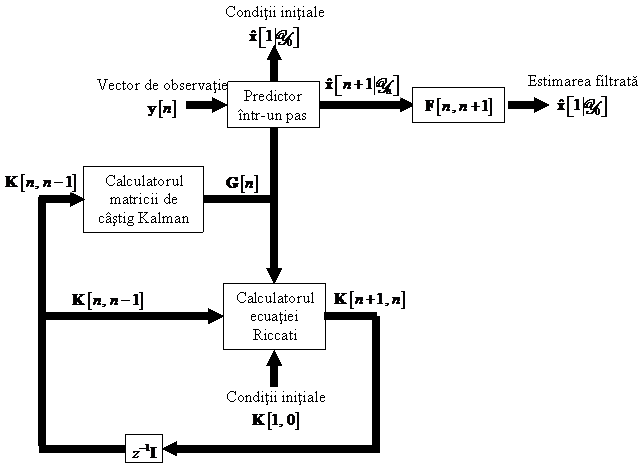
O diagrama bloc a algoritmului de
filtrare Kalman este prezentata in Fig.
11. . Ea se bazeaza pe trei blocuri functionale:
- Calculatorul matricii de castig Kalman, descris prin diagrama din Fig. 11.
- Predictorul Kalman inainte intr-un pas descris prin diagrama din Fig. 11.
- Calculatorul ecuatiei Riccati reprezentat prin diagrama din Fig. 11. .
Principalul motiv al interesului pe care
il aratam teoriei filtrelor Kalman se datoreaza faptului ca ea furnizeaza un
cadru general pentru deducerea unor algoritmi de filtrare adaptiva cunoscuti
sub numele colectiv de familia algoritmilor recursivi a celor mai mici patrate
(RLS). Pentru a evidentia corespondentele dintre filtrarea Kalman si algoritmii
RLS, ne vom focaliza atentia asupra unui model dinamic special de sistem
adaptiv care satisface necesitatile noastre viitoare.

|
Fig. 11. Diagrama bloc a algoritmului de filtrare Kalman bazat pe predictia
inainte intr-un pas
|
Caz special:
Sistem dinamic nefortat
Consideram un sistem dinamic linear a
carui model in spatiul starilor este descris de urmatoarea pereche de ecuatii
de stare:
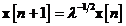
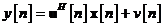
unde 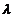 este un scalar real pozitiv. Conform acestui
model, zgomotul de proces este nul iar zgomotul de masurare, reprezentat prin
scalarul
este un scalar real pozitiv. Conform acestui
model, zgomotul de proces este nul iar zgomotul de masurare, reprezentat prin
scalarul 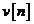 ,
este un proces de zgomot alb de varianta unitara, dupa cum rezulta din relatia
de mai jos
,
este un proces de zgomot alb de varianta unitara, dupa cum rezulta din relatia
de mai jos
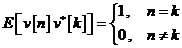
In urma compararii acestui model cu modelul
general descris prin ecuatiile pana la , notam urmatoarele:
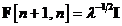
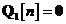
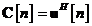
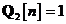
Modelul din spatiul starilor descris prin
ecuatiile pana la este numit model dinamic nefortat datorita faptului ca in
ecuatia de proces lipseste vreo forta externa. Mai important, matricea de tranzitie a
starilor a modelului este egala cu matricea identitate 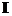 scalata cu constanta
scalata cu constanta 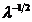 .
In consecinta, matricea de autocorelatie a erorii de predictie a starii
.
In consecinta, matricea de autocorelatie a erorii de predictie a starii 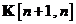 si matricea de autocorelatie a erorii de
filtrare a starii
si matricea de autocorelatie a erorii de
filtrare a starii 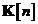 iau o valoare comuna (vezi
relatia
iau o valoare comuna (vezi
relatia
Acest model special constituie cheia
formularii unui cadru general pentru dezvoltarea familiei de algoritmi adaptivi
de filtrare RLS. Dupa cum se va arata mai departe, constanta 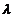 are un rol semnificativ in functionarea
acestor algoritmi.. Vom considera in continuare, cateva variante ale
algoritmului de filtrare Kalman bazate pe modelul dinamic nefortat.
are un rol semnificativ in functionarea
acestor algoritmi.. Vom considera in continuare, cateva variante ale
algoritmului de filtrare Kalman bazate pe modelul dinamic nefortat.
Algoritmul de
filtrare de covarianta (Kalman)
Algoritmul de filtrare Kalman rezumat in Tabela 11. este astfel conceput incat sa propage matricea de
autocorelatie (covarianta) 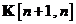 ce se refera la eroarea de estimare a starii
ce se refera la eroarea de estimare a starii 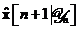 . Acest algoritm este denumit, prin urmare, algoritmul de filtrare
de covarianta (Kalman). Pentru modelul dinamic nefortat pe de alta parte,
gasim ca inlocuind ecuatiile din Tabela 11. se obtine algoritmul simplificat de filtrare de
covarianta, rezumat in Tabela
11. . In acest din urma tabel, se observa ca se utilizeaza
. Acest algoritm este denumit, prin urmare, algoritmul de filtrare
de covarianta (Kalman). Pentru modelul dinamic nefortat pe de alta parte,
gasim ca inlocuind ecuatiile din Tabela 11. se obtine algoritmul simplificat de filtrare de
covarianta, rezumat in Tabela
11. . In acest din urma tabel, se observa ca se utilizeaza
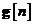 pentru a desemna matricea Kalman de castig,
care in acest caz special ia forma unui vector.
pentru a desemna matricea Kalman de castig,
care in acest caz special ia forma unui vector.
|
Tabela 11. Rezumatul algoritmului de filtrare de covarianta (Kalman) pentru
modelul special dinamic nefortat
Procesul scalar de intrare
Observatii
= 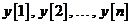
Parametrii cunoscuti
Matricea
de tranzitie a starilor = 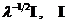 =
matricea identitate =
matricea identitate
Matricea
de masurare = 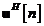
Varianta
zgomotului de masurare 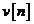 = = 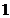
Conditii
initiale
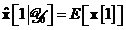
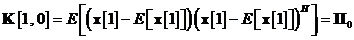
Algoritm de calcul 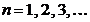
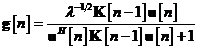
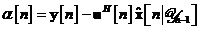
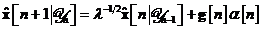
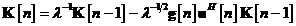
|
Algoritmul de
filtrare informationala
Filtrul Kalman poate fi de asemenea
implementat prin calculul recursiv a matricii inverse 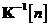 .
In aceasta abordare se poate spune ca se accentueaza caracterul de algoritm RLS
al procesului de filtrare. Inversa matricii de autocorelatie a erorii de
stare
.
In aceasta abordare se poate spune ca se accentueaza caracterul de algoritm RLS
al procesului de filtrare. Inversa matricii de autocorelatie a erorii de
stare 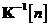 este legata de matricea de informatie a lui
Fisher, fapt care permite sa se dea operatiunii de filtrare o interpretare din
punctul de vedere al teoriei informatiei. Din acest motiv, implementarea
algoritmului de filtrare Kalman, care se bazeaza pe
este legata de matricea de informatie a lui
Fisher, fapt care permite sa se dea operatiunii de filtrare o interpretare din
punctul de vedere al teoriei informatiei. Din acest motiv, implementarea
algoritmului de filtrare Kalman, care se bazeaza pe 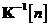 ,
este denumita algoritm de filtrare informationala.
,
este denumita algoritm de filtrare informationala.
Pentru a deduce algoritmul de filtrare
informationala, procedam in maniera descrisa in continuare.
Pasul 1. Se porneste de la ecuatia cu
diferente finite Riccati care, in cazul special al modelului dinamic nefortat,
capata forma (vezi ultima linie din Tabela
11. ):
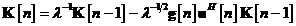
Exprimam din ultima ecuatie valoarea
produsului matricial 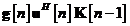
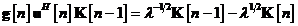
In continuare exprimam, ca in prima linie a
algoritmului din Tabela 11. , valoarea vectorului de castig Kalman pentru modelul
dinamic nefortat
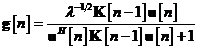
Inmultind si rearanjand termenii, putem
rescrie ecuatia sub forma:
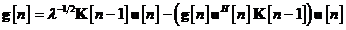
Se obtine astfel o noua definitie a vectorului
de castig Kalman prin inlocuirea relatiei in si simplificarea termenilor comuni
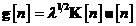
Eliminand in continuare pe 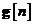 intre ecuatiile si , si multiplicand apoi rezultatul cu
intre ecuatiile si , si multiplicand apoi rezultatul cu 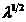 se obtine
se obtine
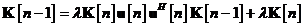
In sfarsit, se inmulteste inainte ecuatia cu matricea inversa 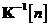 si inapoi cu
si inapoi cu 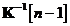 .
Rezultatul care se obtine este prima ecuatie de recursie a algoritmului de
filtrare informationala:
.
Rezultatul care se obtine este prima ecuatie de recursie a algoritmului de
filtrare informationala:
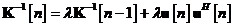
Pasul 2 Conform liniilor doi si trei ale
algoritmului prezentat in Tabela
11. se scrie:
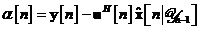
si respectiv
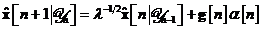
In consecinta, inlocuind ecuatia in , obtinem
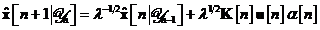
Apoi, eliminarea lui 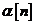 intre ecuatiile si , conduce la
intre ecuatiile si , conduce la
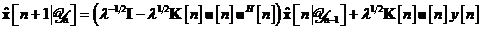
Dar, din ecuatia , se poate deduce cu usurinta urmatoarea relatie:
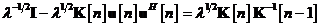
Conform ultimei relatii, ecuatia se poate simplifica dupa cum urmeaza:
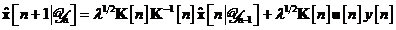
Inmultim inainte aceasta ecuatie cu matricea inversa 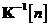 si obtinem cea de a doua relatie de recursie a
algoritmului de filtrare informationala:
si obtinem cea de a doua relatie de recursie a
algoritmului de filtrare informationala:
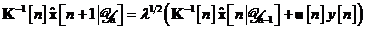
Se poate observa faptul ca prin ecuatia , algoritmul propaga mai degraba produsul 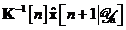 decat estimarea
decat estimarea 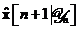 ,
care de fapt prezinta interes.
,
care de fapt prezinta interes.
Pasul 3 In final, valoarea reinnoita a
estimarii vectorului de stare este calculata prin combinarea rezultatelor
pasilor 1 si 2 dupa cum urmeaza:
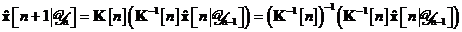
Ecuatiile si , in aceasta ordine, reprezinta algoritmul de filtrare informationala
pentru modelul de sistem dinamic nefortat definit prin relatiile pana la . Un rezumat al algoritmului este prezentat in Tabela 11. .
|
Tabela 11. Rezumatul algoritmului de filtrare informationala pentru modelul
special dinamic nefortat
Procesul scalar de intrare
Observatii = 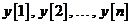
Parametrii cunoscuti
Matricea de
tranzitie a starilor = 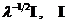 =
matricea identitate =
matricea identitate
Matricea de masurare
= 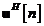
Varianta zgomotului
de masurare 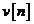 = = 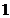
Conditii initiale
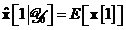
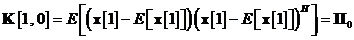
Algoritm de calcul 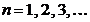
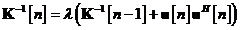
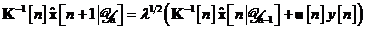
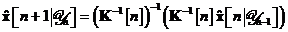
|
Desi implementarile de covarianta si
filtrare informationala a filtrului Kalman, asa cum au fost descrise mai sus,
sunt echivalente algebric, proprietatile lor numerice pot sa difere
substantial. Totusi, ambii algoritmi necesita acelasi numar de operatii
algebrice (adica multiplicari si adunari), ceea ce, pentru modelul special de
sistem examinat este 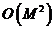 ,
unde
,
unde 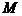 reprezinta dimensiunea vectorului de stare.
reprezinta dimensiunea vectorului de stare.
Pana in acest moment al discutiei noastre
asupra filtrelor Kalman, s-a tratat doar problema estimarii vectorului de stare
pentru un model linear al unui sistem dinamic. Vom arata in prezentul
paragraf ca, si in cazul in care modelul sistemului este nelinear, se
poate aplica filtrarea Kalman prin utilizarea unei proceduri de linearizare.
Vom denumi in mod natural filtrul rezultat in urma acestei operatiuni, filtru
Kalman extins (Extended
Kalman Filter).
O asemenea extindere este fezabila datorita faptului ca filtrul Kalman este
descris, in cazul nostru, prin ecuatii cu diferente finite. Trebuie subliniat
faptul ca o asemenea extindere nu este posibila in cazul filtrului Wiener,
intrucat notiunea de raspuns la impuls (pe care se bazeaza filtrul Wiener) are
sens doar in cazul sistemelor lineare. Aceasta observatie reprezinta un avantaj
major al filtrului Kalman in raport cu filtrul Wiener.
Vom porni in dezvoltarea filtrului Kalman
extins de la modelul linear standard al unui sistem dinamic in spatiul starilor
introdus in prima parte a capitolului (ecuatiile si ), pe care le reproducem in continuare:
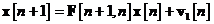
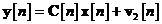
unde 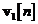 si
si 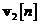 sunt procese de zgomot alb necorelate si cu
media nula si matrici de autocorelatie
sunt procese de zgomot alb necorelate si cu
media nula si matrici de autocorelatie 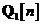 respectiv
respectiv 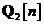 ,
definite prin relatiile si . Ecuatiile de definitie a filtrului Kalman corespunzator sunt rezumate
in Tabela 11. . Vom rescrie aceste ecuatii intr-o forma usor
modificata, mai convenabila scopului propus. In particular, vom realiza
recursia pentru estimarea starii
sistemului in doi pasi. In primul pas se recalculeaza
,
definite prin relatiile si . Ecuatiile de definitie a filtrului Kalman corespunzator sunt rezumate
in Tabela 11. . Vom rescrie aceste ecuatii intr-o forma usor
modificata, mai convenabila scopului propus. In particular, vom realiza
recursia pentru estimarea starii
sistemului in doi pasi. In primul pas se recalculeaza 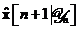 pornind de la
pornind de la 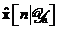 .
In al doilea pas, pornind de la
.
In al doilea pas, pornind de la 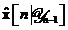 se obtine
se obtine 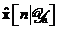 .
Aceasta recursie face apel la inlocuirea ecuatiei in si definirea unei noi matrici de castig Kalman:
.
Aceasta recursie face apel la inlocuirea ecuatiei in si definirea unei noi matrici de castig Kalman:
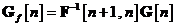
In aceste conditii, algoritmul de filtrare
Kalman este descris prin urmatoarele ecuatii
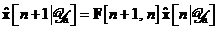
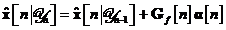
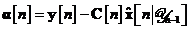

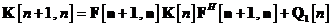
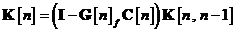
In continuare, vom aborda un model ceva mai elaborat pentru sistemul dinamic. In
loc de ecuatiile de stare si , vom utiliza modelul alternativ:
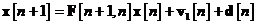
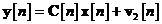
unde 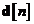 este un vector cunoscut (adica nealeator). Se
verifica usor in acest caz ca ecuatiile Kalman pana la raman nemodificate, exceptie facand prima ecuatie care devine:
este un vector cunoscut (adica nealeator). Se
verifica usor in acest caz ca ecuatiile Kalman pana la raman nemodificate, exceptie facand prima ecuatie care devine:
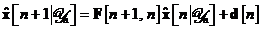
Aceasta modificare va fi utilizata la
deducerea filtrului Kalman extins ce va fi efectuata in continuare.
Dupa cum a fost mentionat inainte,
filtrul Kalman extins (EKF) este o solutie aproximativa care ofera
posibilitatea extinderii principiului de filtrare Kalman la modele nelineare
in spatiul starilor. In particular, modelul nelinear, pe care il vom considera
in continuare, are urmatoarea forma:
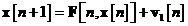
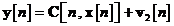
unde, ca si mai sus, 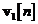 si
si 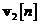 sunt procese de zgomot alb necorelate si cu
media nula si matrici de autocorelatie
sunt procese de zgomot alb necorelate si cu
media nula si matrici de autocorelatie 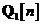 respectiv
respectiv 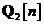 .
In schimb, aici, functionala
.
In schimb, aici, functionala 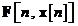 reprezinta o matrice de tranzitie nelineara,
posibil variabila in timp.. In cazul linear, ea se reduce pur si simplu la
cazul tratat anterior
reprezinta o matrice de tranzitie nelineara,
posibil variabila in timp.. In cazul linear, ea se reduce pur si simplu la
cazul tratat anterior
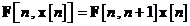
In schimb, in cazul general nelinear, prin
actiunea functionalei 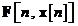 componentele vectorului de stare
componentele vectorului de stare 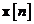 pot fi combinate nelinear. Mai mult, aceasta
dependenta nelineara poate fi si variabila in timp. Similar, functionala
pot fi combinate nelinear. Mai mult, aceasta
dependenta nelineara poate fi si variabila in timp. Similar, functionala 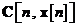 reprezinta o matrice de masurare nelineara
care, de asemenea, poate fi variabila in timp.
reprezinta o matrice de masurare nelineara
care, de asemenea, poate fi variabila in timp.
Drept exemplu, sa consideram urmatorul
model bidimensional in spatiul starilor pentru relatia
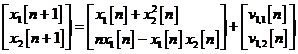
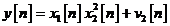
In acest exemplu avem
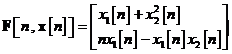
si
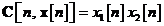
Ideea fundamentala a filtrului Kalman
extins consta in linearizarea modelului in spatiul starilor din
ecuatiile si la fiecare moment de timp in jurul celei mai recente estimari de
stare, care poate fi atat 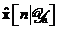 cat si
cat si 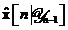 ,
in functie de forma particulara a functionalei utilizate.. Odata obtinut
modelul linear, se aplica ecuatiile standard ale filtrului Kalman.
,
in functie de forma particulara a functionalei utilizate.. Odata obtinut
modelul linear, se aplica ecuatiile standard ale filtrului Kalman.
Mai explicit, aproximarea se face in doi
pasi.
Pasul 1. Se construiesc urmatoarele doua
matrici
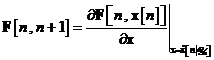
si
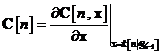
Drept urmare, componenta 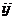 a lui
a lui 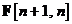 este egala cu derivata partiala a componentei
este egala cu derivata partiala a componentei 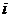 a lui
a lui 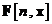 in raport cu componenta
in raport cu componenta 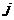 a lui
a lui 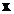 .
Similar, componenta
.
Similar, componenta 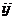 a lui
a lui 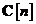 este egala cu derivata partiala a componentei
este egala cu derivata partiala a componentei 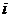 a lui
a lui 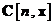 in raport cu componenta
in raport cu componenta 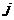 a lui
a lui 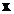 .
In primul caz, derivatele sunt evaluate in
.
In primul caz, derivatele sunt evaluate in 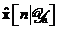 ,
in timp ce in al doilea caz, derivatele se evalueaza la
,
in timp ce in al doilea caz, derivatele se evalueaza la 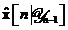 .
Componentele matricilor
.
Componentele matricilor 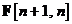 si
si 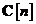 sunt cunoscute cu toate (adica sunt
calculabile), pentru ca
sunt cunoscute cu toate (adica sunt
calculabile), pentru ca 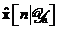 si
si 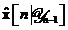 sunt cunoscute asa cum se arata in continuare.
sunt cunoscute asa cum se arata in continuare.
Aplicam definitiile si la exemplul ales si obtinem
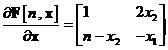
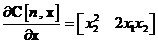
ceea ce conduce la
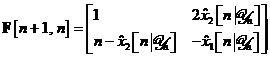
si
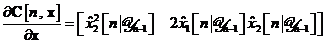
Pasul 2 Odata facuta evaluarea matricilor 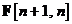 si
si 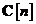 ,
acestea sunt utilizate in continuare la stabilirea aproximatiei Taylor de
ordinul intai a functionalelor nelineare
,
acestea sunt utilizate in continuare la stabilirea aproximatiei Taylor de
ordinul intai a functionalelor nelineare 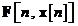 si
si 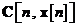 in jurul valorilor
in jurul valorilor 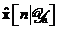 si
si 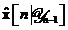 .
In particular,
.
In particular, 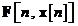 si
si 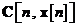 se aproximeaza dupa cum urmeaza:
se aproximeaza dupa cum urmeaza:
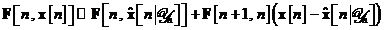
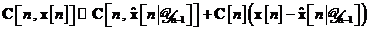
Pe baza ultimelor doua relatii, se poate
acum purcede la aproximarea ecuatiilor de stare nelineare si prin expresiile care urmeaza:
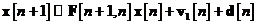
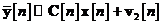
In si s-au introdus doua noi cantitati:
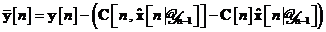
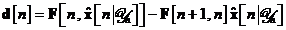
Componentele vectorului 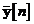 sunt toate cunoscute la momentul de timp
sunt toate cunoscute la momentul de timp 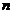 ,
si, prin urmare,
,
si, prin urmare, 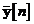 poate fi privit ca un vector de observatie la
momentul
poate fi privit ca un vector de observatie la
momentul 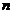 .
Similar, si toate componentele vectorului
.
Similar, si toate componentele vectorului 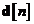 se cunosc la momentul
se cunosc la momentul 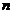 .
.
Modelul de stare aproximativ descris de ecuatiile si este linear si are o forma matematica identica cu modelul descris prin
ecuatiile si ; de fapt, cu acest obiectiv in vedere s-a formulat mai devreme modelul
din ecuatiile si . Ecuatiile filtrului Kalman extins sunt, prin urmare, si in acest caz,
ecuatiile Kalman standard pana la si aplicate modelului linear definit mai sus. Se ajunge la urmatorul set
de ecuatii:
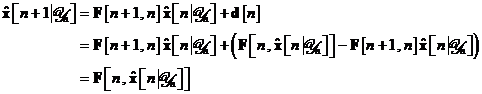
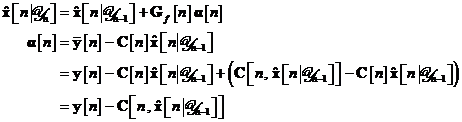
Pe baza ecuatiilor si poate fi acum reprezentat graful de semnal din Fig.
11. a operatiei de reinnoire a predictiei cu un pas la
filtrul Kalman extins.
Tabela
11. 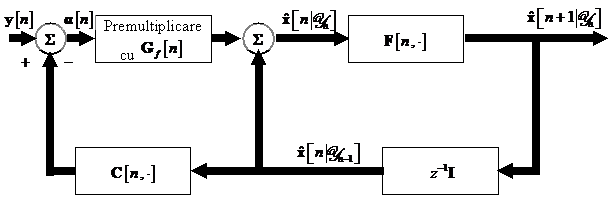 prezinta un rezumat a algoritmului
de filtrare Kalman extins, in care matricile linearizate
prezinta un rezumat a algoritmului
de filtrare Kalman extins, in care matricile linearizate 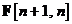 si
si 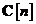 sunt calculate din omoloagele lor nelineare pe
baza ecuatiilor si . Fiind dat un model de sistem in spatiul starilor descris prin
ecuatiile si , se poate utiliza acest algoritm pentru a calcula estimarea de stare
recursiv. Comparand ecuatiile filtrului Kalman extins rezumate aici cu
ecuatiile filtrului Kalman standard date prin relatiile pana la , observam faptul ca singurele diferente dintre ele apar la calculul
vectorului de inovatii
sunt calculate din omoloagele lor nelineare pe
baza ecuatiilor si . Fiind dat un model de sistem in spatiul starilor descris prin
ecuatiile si , se poate utiliza acest algoritm pentru a calcula estimarea de stare
recursiv. Comparand ecuatiile filtrului Kalman extins rezumate aici cu
ecuatiile filtrului Kalman standard date prin relatiile pana la , observam faptul ca singurele diferente dintre ele apar la calculul
vectorului de inovatii 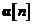 si a estimarii vectorului de stare
si a estimarii vectorului de stare 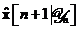 .
In detaliu, termenii lineari
.
In detaliu, termenii lineari 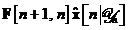 si
si 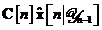 de la filtrul Kalman standard sunt inlocuiti
prin termenii aproximativi
de la filtrul Kalman standard sunt inlocuiti
prin termenii aproximativi 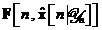 si
si 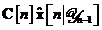 respectiv de la filtrul Kalman extins. Aceste diferente sunt de asemenea puse in
evidenta la compararea grafului de semnal din Fig.
11. pentru predictia intr-un pas facuta cu filtrul Kalman
standard si cel din Fig. 11. pentru predictia intr-un pas facuta cu filtrul Kalman
extins.
respectiv de la filtrul Kalman extins. Aceste diferente sunt de asemenea puse in
evidenta la compararea grafului de semnal din Fig.
11. pentru predictia intr-un pas facuta cu filtrul Kalman
standard si cel din Fig. 11. pentru predictia intr-un pas facuta cu filtrul Kalman
extins.
|
Fig. 11. Graful de semnal a predictorului intr-un pas a
filtrului Kalman extins
|
|
Tabela 11. Rezumatul filtrului Kalman extins
Vectorul procesului de intrare
Observatii = 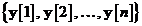
Parametrii cunoscuti
Matricea de
tranzitie a starilor = 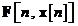
Matricea de masurare
= 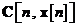
Matricea de
autocorelatie a vectorului de zgomot de proces = 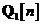
Matricea de
autocorelatie a zgomotului de masurare = 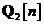
Algoritm de calcul 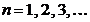

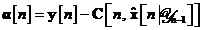
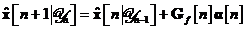
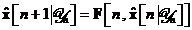
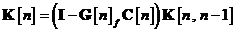
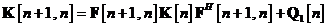
Observatie: Matricile
linearizate 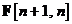 si si 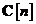 sunt calculate din omoloagele lor nelineare sunt calculate din omoloagele lor nelineare 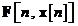 si si 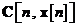 prin utilizarea relatiilor si, respectiv, prin utilizarea relatiilor si, respectiv,
Conditii initiale
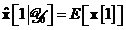
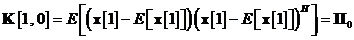
|
Algoritmul
RLS ponderat exponential a fost dedus pe baza principiilor enuntate in
paragraful 10.3. Modelul matematic ce serveste drept fundament acestei deduceri
este deterministic, intrucat singura sa sursa de incertitudine rezida in
caracterul aleator al erorii de masurare 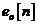 .
Algoritmul RLS poate fi de asemenea dedus exact direct din algoritmul de
filtrare Kalman de covarianta prezentat in paragraful 11.7, utilizand un model in spatiul starilor care se
adapteaza perfect problemei RLS. Modelul de stare utilizat aici este prin
formularea sa natural stochastic. Aceasta abordare alternativa fata de solutia
problemei RLS este deosebit de importanta intrucat ne permite sa stabilim o
lista de corespondente unu la unu intre variabilele RLS si variabilele Kalman
bazate pe modelul de stare. Cu o asemenea lista la dispozitie, putem utiliza
vasta literatura consacrata filtrelor Kalman pentru a rezolva problema RLS
intr-o maniera unificata, ceea ce reprezinta obiectivul nostru final.
.
Algoritmul RLS poate fi de asemenea dedus exact direct din algoritmul de
filtrare Kalman de covarianta prezentat in paragraful 11.7, utilizand un model in spatiul starilor care se
adapteaza perfect problemei RLS. Modelul de stare utilizat aici este prin
formularea sa natural stochastic. Aceasta abordare alternativa fata de solutia
problemei RLS este deosebit de importanta intrucat ne permite sa stabilim o
lista de corespondente unu la unu intre variabilele RLS si variabilele Kalman
bazate pe modelul de stare. Cu o asemenea lista la dispozitie, putem utiliza
vasta literatura consacrata filtrelor Kalman pentru a rezolva problema RLS
intr-o maniera unificata, ceea ce reprezinta obiectivul nostru final.
Compararea modelelor aleatoare si deterministe
Pentru inceput, vom considera modelul dinamic nefortat descris prin
ecuatiile pana la , reprodus in continuare
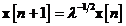
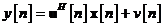
unde 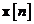 este vectorul de stare a modelului,
este vectorul de stare a modelului, 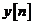 este marimea scalara de obsevatie sau semnalul
de referinta, iar
este marimea scalara de obsevatie sau semnalul
de referinta, iar 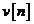 este un proces scalar aleator de zgomot alb de
medie nula si varianta unitara. Parametrul modelului
este un proces scalar aleator de zgomot alb de
medie nula si varianta unitara. Parametrul modelului 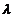 este o constanta reala si pozitiva. Din
relatia se vede usor ca:
este o constanta reala si pozitiva. Din
relatia se vede usor ca:
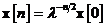
unde 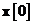 este valoarea initiala a vectorului de stare.
Evaluand in consecinta ecuatia la momentele
este valoarea initiala a vectorului de stare.
Evaluand in consecinta ecuatia la momentele 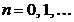 ,
si utilizand in continuare ecuatia pentru a exprima vectorii de stare la momente distincte in functie de
valoarea initiala
,
si utilizand in continuare ecuatia pentru a exprima vectorii de stare la momente distincte in functie de
valoarea initiala 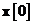 ,
se obtine urmatorul sistem de ecuatii lineare simultane:
,
se obtine urmatorul sistem de ecuatii lineare simultane:
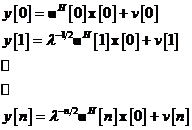
Echivalent, putem scrie
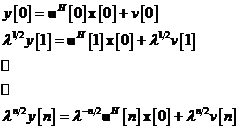
Sistemul de ecuatii reprezinta o caracterizare stochastica a modelului dinamic nefortat,
corespunzand astfel la o abordare din punct de vedere Kalman a problemei.
Vom considera in continuare formularea determinista a problemei, adica
vom incerca sa o privim din punctul de vedere RLS. Adaptand la problema
examinata modelul de regresie lineara din ecuatia (10.43):
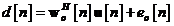
putem scrie urmatorul sistem
determinist de ecuatii lineare simultane:
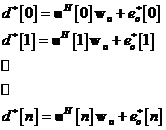
unde 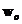 este vectorul de parametri necunoscuti ai
modelului,
este vectorul de parametri necunoscuti ai
modelului, 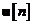 este vectorul de intrare,
este vectorul de intrare, 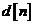 este semnalul de referinta sau raspunsul dorit
iar
este semnalul de referinta sau raspunsul dorit
iar 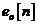 este eroarea de masurare.
este eroarea de masurare.
|
Tabela 11. Corespondente intre variabile Kalman si variabile RLS
|
Kalman
|
RLS
|
|
Descriere
|
Variabila
|
Variabila
|
Descriere
|
|
Valoarea initiala a vectorului de
stare
|
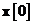
|
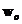
|
Vectorul necunoscut al
coeficientilor filtrului
|
|
Vectorul de stare
|
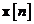
|
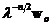
|
Versiunea ponderata exponential al
vectorului necunoscut al coeficientilor filtrului
|
|
Semnalul de referinta (observat)
|
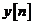
|
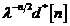
|
Raspunsul dorit
|
|
Zgomotul de masurare
|
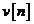
|
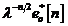
|
Eroarea de masurare
|
|
Vectorul de stare a predictiei
intr-un pas
|
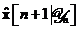
|
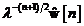
|
Estimarea vectorului coeficientilor
|
|
Matricea de corelatie a erorii in
predictia de stare
|
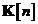
|
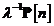
|
Inversa matrici de corelatie a
vectorului de intrare
|
|
Vectorul de castig Kalman
|
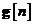
|
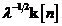
|
Vectorul de castig
|
|
Inovatie
|
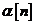
|
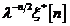
|
Eroarea de estimare apriori
|
|
Factorul de conversie
|
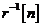
|
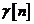
|
Factorul de conversie
|
|
Conditiile initiale
|
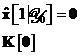
|
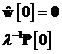
|
Conditiile initiale
|
|
Avem astfel doua
sisteme de ecuatii lineare simultane pentru rezolvarea in esenta a aceleiasi
probleme. Un sistem este stochastic, bazat pe teoria filtrului Kalman; celalalt
sistem este determinist, bazat pe teoria estimarii dupa cele mai mici patrate.
Intuitiv, ne-am astepta ca ambele abordari sa conduca exact la aceiasi solutie
pentru problema examinata. mai mult, recunoscand ca aceste doua sisteme de
ecuatii au aceiasi forma matematica, pare rezonabil pentru noi sa fixam
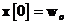
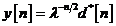
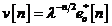
unde asteriscul reprezinta conjugarea
complexa, variabilele din membrii stangi se refera la modelul din spatiul starilor,
iar cele din membrii drepti se refera la modelul de regresie lineara.
Comparatie
intre filtrul Kalman de covarianta si a algoritmului RLS
Vom extinde in
continuare lista de corespondente intre cele doua metode, comparand algoritmul
de filtrare de covarianta Kalman din Tabela
11. si algoritmul RLS prezentat in Tabel 10.1 din capitolul
10. Facand comparatia linie cu linie a celor doi algoritmi si presupunand ca in
Tabela 11. se ia 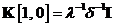 si
si 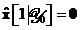 ,
se obtine:
,
se obtine:
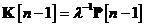
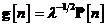
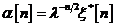
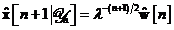
Mai mult, compararea ecuatiilor si (10.37) evidentiaza faptul ca factorul de conversie 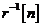 din forma specializata a algoritmului de filtrare Kalman de covarianta si factorul
de conversie
din forma specializata a algoritmului de filtrare Kalman de covarianta si factorul
de conversie 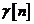 din algoritmul RLS sunt identici:
din algoritmul RLS sunt identici:
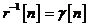
Intr-adevar, adaptand ecuatia la forma specializata a algoritmului de filtrare Kalman din Tabela 11. , avem
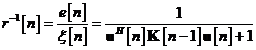
Tabela 11. prezinta corespondentele dintre variabilele utilizate
de cei doi algoritmi. Partea stanga a tabelei prezinta variabilele Kalman si
descrierea lor iar partea dreapta contine variabilele RLS.
Filtrul Kalman este un sistem in timp
discret, linear, de dimensiuni finite, a carui implementare se adecveaza bine
calculatorului electronic. O proprietate fundamentala a filtrului Kalman este
aceea ca el conduce la minimizarea urmei matricii de autocorelatie a erorii de
stare filtrate 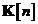 .
Aceasta, inseamna ca filtrul Kalman este estimatorul linear de varianta
minima a vectorului de stare
.
Aceasta, inseamna ca filtrul Kalman este estimatorul linear de varianta
minima a vectorului de stare 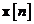 .
.
Filtrul Kalman a fost utilizat cu succes
la rezolvarea multor probleme tehnice si stiintifice. Mai mult, filtrul Kalman
furnizeaza cadrul general pentru dezvoltarea tuturor algoritmilor cunoscuti din
familia filtrelor adaptive RLS. Acest lucru a fost demonstrat intr-o lucrare
din 1994 a lui Sayed si Kailath. Drept urmare, s-a aratat perfecta echivalenta
dintre problemele intalnite in filtrarea adaptiva a semnalelor si cele
rezolvate prin filtrare Kalman in automatica. S-a deschis astfel calea
aplicarii si in prelucrarea digitala a semnalelor a acestor rezultate.


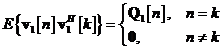





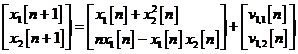
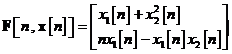
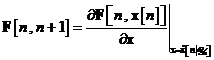
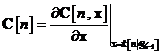
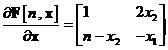
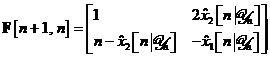
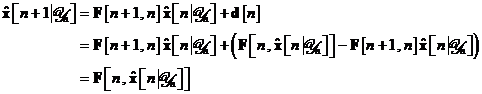
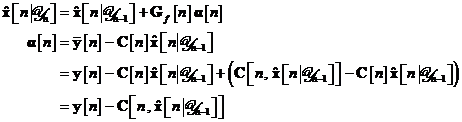
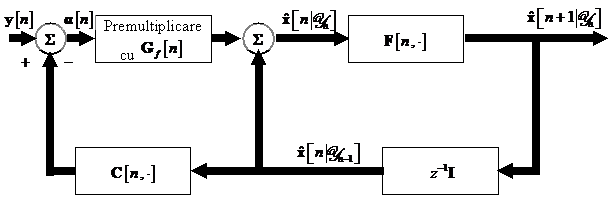 prezinta un rezumat a algoritmului
de filtrare Kalman extins, in care matricile linearizate
prezinta un rezumat a algoritmului
de filtrare Kalman extins, in care matricile linearizate