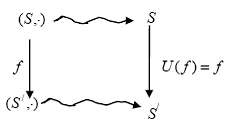Functori

Functori

Atunci cand definim o categorie se surprinde numai o parte particulara a structurii si obiectelor componente.In plus, pot exista, pentru o aceeasi clase de obiecte, mai multe notiuni de structura. De exemplu, in cazul dezvoltarii orientate obiect, avem o structura care descrie modul de interconectare al obiectelor in sisteme precum si o structura care surprinde rafinarea obiectelor.

De asemenea, pot exista relatii pe care le dorim a fi studiate intre doua domenii complet diferite, cum ar fi intre specificarea unui limbaj de programare si categoria proceselor.

Definitia 2. 1:

Fiind date doua categorii C    si D , un functor F : C 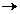  D consta in operatiile F : C → D si F : C → D astfel incat, pentru fiecare f : X → Y, F (f ) : F (X) → F (Y) si

pentru X 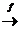Y 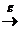Z F (g o f) = F (g) o F (f);

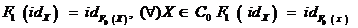pentru fiecare X C

De obicei scriem doar F in loc de F , F

Asadar, rolul functorilor in teoria categoriilor este asemanator celui jucat de homomorfism intre structuri algebrice (grupuri, monoizi, s.a.m.d.).

Exemple de functori :

. Exista un functor U: Top → Set care atribuie oricarui spatiu topologic X, multimea X. 

Similar, exista si functorii "uituci" Grp Set, Graph Set, Rng Set, Pos Set

Sgr Set

U: Sgr Set

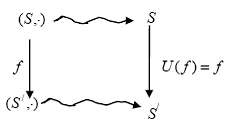
Pentru fiecare categorie C, exista un functor unic C 1 si un alt functor unic 0 C

Putem defini un functor P Set Set power set functor) care asociaza fiecarei multimi A

multimea tuturor submultimilor sale P A

Fie doua categorii C si D Putem defini categoria produs C D care are:

obiecte: perechile (C D ∈

morfisme: (C D (C',D' perechile ( f g) cu f C C' in C si g D D in D

Exista functorii  :C D C si  : C D D , care duc obiectele si morfismele lui C D in C, respectiv D

Fie doi functori F: C 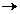 D si G: D 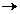C. Se poate defini compunerea G o F: C  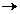C Aceasta compunere este asociativa si cum avem, pentru orice categorie e, functorul identitate C  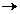C atunci exista categoria Cat a tuturor categoriilor, care are ca obiecte categoriile, iar ca morfisme functorii.

Orice graf orientat poate fi privit ca o categorie astfel: obiectele sunt nodurile, iar morfismele sunt drumurile in graf. Se defineste un functor de la categoria Dgraph a grafurilor orientate la Cat. Imaginea unui graf orientat D prin acest functor se numeste categoria generat de graful D.

Multe operatii asupra multimilor sunt "functoriale", adica ele nu actioneaza doar asupra multimilor, ci si asupra functiilor dintre multimi, intr-o maniera potrivita. Acest lucru este familiar si informaticii folosindu-se insa nu terminologia din teoria categoriilor, ci de termenul de functie. Sa exemplificam:

Fie Set categoria multimilor si List categoria listelor. Putem defini un functor intre aceste categorii astfel:

Daca A este o multime, ii asociem list (A) in categoria List, unde list(A) descrie multimea listelor finite de elemente ale lui A (clar izomorf cu A*);

pentru functia f : A -> B, putem defini o functie list (A) -> list (B) intre multimile similare de liste, care este numita de obicei map_list (f); ea transforma o lista finita de elemente ale lui A, [ a1, , an], in lista [f (aj, , f (an)] de elemente din B.

Nu este greu de aratat ca aceasta operatie map_list pastreaza functiile identitate si compunerea functiilor, adica:

si map_list(g o f = map_list (g) o map_list (f)

In continuare ne vom concentra pe astfel de functorialitate la cateva operatii de baza, cum ar fi produsul coprodusul (reuniunea disjuncta) si powerset-ul (multimea partilor).

Doua multimi X Y produsul cartezian X Y este multimea de perechi: X Y =

Exista, evident, proiectiile

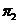X Y X   si X Y Y

date prin relatiile:

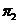x y x si x y y

De asemenea, pentru functiile: f Z X si g Z Y , exista o "functie pereche" unica:

f, g Z X Y , cu f g f si 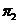f, g g si anume:

f, g z f z g z X Y z Z

Observatie:

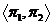=id : X×Y→X×Y

f, g 〉 h f h g h W X Y , pentru h W → Z

Interesant este ca produsul cartezian nu se aplica doar pentru multimi ci si pentru functii.

Pentru functiile f X → X′ si g Y → Y′ putem defini o functie pe X X′ → Y Y′ prin relatia:

x y f x g y

Aceasta functie se poate scrie: f g : X Y → X′ Y′ , unde simbolul " " este folosit si la multimi si la functii.

Se observa ca f g poate fi descrisa in termeni de proiectie si pereche astfel:

f×g

Se verifica usor ca operatia " " asupra functiilor satisface relatiile:

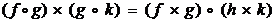
Aceasta ne demonstreaza ca produsul " " este functorial: adica nu se aplica doar multimilor, ci si

functiilor si face ca astfel sa se pastreze aplicatiile identitate si compunerea.

Putem da ca exemplu coprodusul (sau reuniunea disjuncta, sau suma

Pentru multimile X Y, scriem reuniunea lor disjuncta ca X Y

Explicit: X Y

Primele componente: 0 si 1 "forteaza" ca aceasta reuniune sa fie disjuncta. Acestea ne

permit sa recunoastem elementele lui X si ale lui Y, in coprodusul X Y. In loc de proiectii (ca mai

sus), vorbim acum de "coproiectii

X X Y si Y X Y