Idealele si inelele
factor ale inelului Z
Deoarece orice ideal este subgrup al
grupului aditiv al inelului, rezulta ca idealele lui Z sunt printre
subgrupurile grupului aditiv al lui Z, care, dupa cum stim,
sunt de forma n Z, cu n ≥ 0. Se observa
insa ca subgrupurile n Z ale lui Z sunt toate ideale ale
lui Z, deci idealele lui Z coincid cu subgrupurile grupului aditiv al lui Z si sunt toate
ideale principale.
Suma
a doua ideale n Z si m Z este idealul generat de cel mai
mare divizor comun al numerelor m si n pe care il notam cu (n, m). In adevar,
daca nZ + mZ = qZ,
q
≥ 0, atunci din faptul ca n qZ si m
qZ si m qZ rezulta
ca q divide pe n, respectiv m, adica q divide pe (n, m). Pe de alta parte,
rezulta ca q = ns +
mt, s,t
qZ rezulta
ca q divide pe n, respectiv m, adica q divide pe (n, m). Pe de alta parte,
rezulta ca q = ns +
mt, s,t  Z, deci orice divizor comun al lui n si m divide si pe q. Asadar, (n, m) divide pe q, de unde rezulta
egalitatea ceruta. In mod analog se arata ca nZ mZ [n, m]Z, unde am notat cu [n, m] cel mai mic multiplu
comun al numerelor n si m. De asemenea, rezulta ca produsul idealelor nZ si mZ este generat de produsul nm. Reamintim ca
doua numere intregi n, m se numesc prime intre ele (sau relativ prime) daca 1 este cel mai
mare divizor comun al lor.
Z, deci orice divizor comun al lui n si m divide si pe q. Asadar, (n, m) divide pe q, de unde rezulta
egalitatea ceruta. In mod analog se arata ca nZ mZ [n, m]Z, unde am notat cu [n, m] cel mai mic multiplu
comun al numerelor n si m. De asemenea, rezulta ca produsul idealelor nZ si mZ este generat de produsul nm. Reamintim ca
doua numere intregi n, m se numesc prime intre ele (sau relativ prime) daca 1 este cel mai
mare divizor comun al lor.
Din
cele de mai sus rezulta ca inelele factor ale lui Z sunt de forma:
Zn = Z/nZ.
Acestea sunt inele comutative cu
element unitate si Zn are n elemente pentru n
> 0. Pentru n Z 0 este izomorf cu Z.
Vom
demonstra cateva proprietati ale inelelor Zn precum si cateva
aplicatii ale acestora.
Propozitia 3.1. In inelul Zn, n >
1, un element 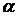 este inversabil
daca si numai daca exista a
este inversabil
daca si numai daca exista a  Z, a relativ prim cu n, astfel incat p(a)
Z, a relativ prim cu n, astfel incat p(a) 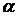 unde p : Z
unde p : Z  Zn este surjectia canonica. In particular,
daca n este prim, orice element nenul din Zn este inversabil.
Zn este surjectia canonica. In particular,
daca n este prim, orice element nenul din Zn este inversabil.
Demonstratie. A doua afirmatie a propozitiei rezulta din
prima. Pentru a demonstra prima afirmatie vom observa ca daca a Z si are proprietatea ca
este relativ prim cu n adica (a, n) = 1, atunci, pentru
orice a'
Z si are proprietatea ca
este relativ prim cu n adica (a, n) = 1, atunci, pentru
orice a' Z cu a' ≡ a mod n avem de asemenea (a',n) = 1. In adevar,
daca un numar divide pe a' si n atunci el divide pe a,
caci acesta are forma a'+ kn, cu k
Z cu a' ≡ a mod n avem de asemenea (a',n) = 1. In adevar,
daca un numar divide pe a' si n atunci el divide pe a,
caci acesta are forma a'+ kn, cu k Z .Daca a este un reprezentant al lui
Z .Daca a este un reprezentant al lui 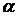 si (a, n) = 1, atunci, dupa
cum am observat mai sus, exista b,
c
si (a, n) = 1, atunci, dupa
cum am observat mai sus, exista b,
c Z astfel incat ab + nc = 1. Trecand
aceasta relatie in Zn, se obtine ca
Z astfel incat ab + nc = 1. Trecand
aceasta relatie in Zn, se obtine ca 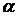 p(b) = 1, deci p(b) este inversul lui
p(b) = 1, deci p(b) este inversul lui 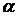 . Reciproc
sa presupunem ca
. Reciproc
sa presupunem ca 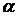
 Zn
Zn
este inversabil, deci exista β Zn astfel incat
Zn astfel incat 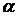 β = 1.Daca, a, b
β = 1.Daca, a, b Z sunt astfel incat p(a) =
Z sunt astfel incat p(a) =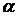 p(b) = β, atunci rezulta ca ab mod n,de unde rezulta ca (a, n)
p(b) = β, atunci rezulta ca ab mod n,de unde rezulta ca (a, n)
Propozitia
3.2. Fie m,n > 1 numere intregi, prime intre ele. Atunci inelul Zn Zm este
izomorf cu Zmn.
Zm este
izomorf cu Zmn.
Demonstratie. Fie pm : Z  Zm, pn : Z
Zm, pn : Z  Zn, pmn : Z
Zn, pmn : Z  Zmn, surjectiile canonice si p' : Z
Zmn, surjectiile canonice si p' : Z  Zm
Zm  Zn aplicatia definita prin p'( a )=( pm( a ), pn( a)).
Aplicatia p' este un morfism de
inele, dupa cum se verifica cu usurinta, iar Ker p' = mn Z .In adevar, mn Z
Zn aplicatia definita prin p'( a )=( pm( a ), pn( a)).
Aplicatia p' este un morfism de
inele, dupa cum se verifica cu usurinta, iar Ker p' = mn Z .In adevar, mn Z Ker p'.
Ker p'.
Fie x Ker p'. Atunci pm(
Ker p'. Atunci pm( ) = 0 si pn(
) = 0 si pn( ) = 0, deci
) = 0, deci  se divide
cu m si cu n si cum (m,n) = 1 rezulta ca x se divide cu produsul mn , adica
se divide
cu m si cu n si cum (m,n) = 1 rezulta ca x se divide cu produsul mn , adica 
 mn Z si Ker p'
mn Z si Ker p' mn Z . Din propozitia 2.7 rezulta ca exista un morfism
injectiv de inele p : Zmn
mn Z . Din propozitia 2.7 rezulta ca exista un morfism
injectiv de inele p : Zmn  Zm x Zn si.deoarece inelele Zmn si Zm
x Zn au acelasi numar de elemente.
rezulta ca p este si surjectiv.
Zm x Zn si.deoarece inelele Zmn si Zm
x Zn au acelasi numar de elemente.
rezulta ca p este si surjectiv.
Fie φ ׃ N  N functia
definita prin:
N functia
definita prin:
φ(0)
= 0, φ(1) = 1 si φ(n) =
numarul numerelor naturale nenule, prime cu n si mai mici decat n, pentru n > 1 . Aplicatia
φ se numeste funcsia lui Euler sau indicatorul lui Euler. Din
propozitia 3.1 rezulta ca Zn coincide cu numarul
elementelor inversabile din inelul Zn, daca n ≥ 1.
Propozitia 3.4. Daca m si n sunt numere naturale prime intre ele,
atunci φ(mn) = φ(m) φ(n).
Demonstratie. Daca
unul din numerele m, n este nul,afirmatia este
evidenta. In caz contrar, mn) coincide cu numarul elementelor
inversabile din inelul Zm x Zn dupa cum rezulta din
propozitia precedenta. Acum afirmatia propozitiei
rezulta din lema care urmeaza si a carei demonstratie
este imediata.
Lema
3.5. Fie A
si B doua inele unitare. Notam cu A*, B* si (AxB )*
respectiv, grupul multiplicativ al elementelor inversabile din A, B si AxB. Atunci exista egalitatea (AxB )* = A* x B*.
Propozitia
3.6. Fie n > 1 un numar intreg si n
= 
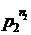 .
.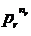 descompunerea sa in produs de numere prime, unde
descompunerea sa in produs de numere prime, unde 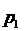 ,
, ,.
,. sunt numere prime distincte. Atunci φ(n) = ( 1 -
sunt numere prime distincte. Atunci φ(n) = ( 1 - 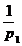 ) ( 1
-
) ( 1
- 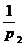 ) .. ( 1 -
) .. ( 1 - 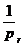 ).
).
Demonstratie Din propozitia 3.4 rezulta
ca φ(n) = φ( φ(
φ(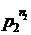 )φ(
)φ(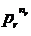 ) Atunci este
suficient sa aratam ca φ(
) Atunci este
suficient sa aratam ca φ( )
)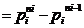 , ceea ce rezulta din faptul
ca numerele naturale mai mici decat
, ceea ce rezulta din faptul
ca numerele naturale mai mici decat
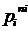 si
care se divid cu
si
care se divid cu 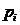 sunt in
numar de
sunt in
numar de  , anume 0,
, anume 0, 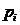 ,2
,2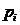 ,.,(
,.,(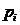 -1)
-1) 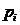 ,
,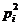 ,,(
,,(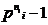 )
)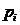
Propozitia 3.7 ( Teorema lui Euler). Daca a si n>0 sunt numere intregi prime
intre ele, atunci

Demonstratie. Deoarece grupul multiplicativ al
elementelor inversabile din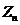 are
ordinul
are
ordinul  , iar
clasa a a lui
a apartine acestui grup,
rezulta ca
, iar
clasa a a lui
a apartine acestui grup,
rezulta ca 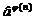 =
= , relatie care este echivalenta cu afirmatia
propozitiei.
, relatie care este echivalenta cu afirmatia
propozitiei.
Pentru
n numar
prim, avem (n)=n-1 si se obtine din propozitia
precedenta urmatorul corolar cunoscut sub numele de Teorema lui
Fermat sau mica teorema a lui Fermat.
Corolarul 3.8 Daca
p>1 este un numar intreg prim
si a un intreg care nu se divide
cu p ,atunci 

