Inele de polinoame
Inelul
polinoamelor intr-o nedeterminata.
Fie A un inel comutativ si unitar. Vom face o
constructie a inelului de polinoame intr-o nedeterminata peste A,
care la inceput nu foloseste scrierea obisnuita a polinoamelor cu
ajutorul unei nedeterminate X.
Peste inelul A se considera
sirurile f = (a0, a1, a2, . ), ai IA a.i.
toti termenii sai, in afara de un numar finit dintre ei, sunt
nuli.
Fie A' multimea tuturor sirurilor
de acest tip. Sirurile f = (a0, a1 , . ) si g = (b0 , b1 , . ) sunt egale daca si
numai daca ai = bi, pentru orice i. Pentru A' se definesc doua operatii
algebrice , adunarea si inmultirea, in raport cu care A' devine un inel
comutativ si unitar.
Fie
f, g IA', f = (a0, a1, a2, . ) , g = (b0, b1, b2, . ).
Atunci adunarea se defineste astfel: f + g = (a0 + b0, a1 + b1, a2 + b2, . ).
Este evident ca f + g are numai un numar finit de termeni
nenuli, deci f + g I A . Sa
verificam ca (A',+) este grup abelian .
Intr-adevar , daca f ,g, h I A , f = (a0, a1, a2, . ), g = (b0,
b1, b2, . ), h = (c0, c1,
c2, . ), atunci (f + g) + h = (a0 + b0,
a1 + b1, a2 + b2, . ) + + (c0, c1, c2, . ) = [(a0 + b0) + c0, (a1 + b1) + c1, . ] si f + (g + h) = (a0, a1, a2, . ) + [(b0, b1, b2,
. ) + (c0, c1, c2, . )] = [a0 + (b0 + c0),a1 + (b1 + c1), . ] .
Cum adunarea in inelul A este asociativa
,avem (ai + bi) + ci = ai + (bi + ci) , i = 1, 2, 3 . , de unde (f + g) + h = f
+ (g + h) . Analog se arata ca f + g = g + f.
Daca 0 = (0, 0, 0, . ) , atunci 0 + f = (0, 0,
. ) + (a0, a1, . ) = (0 + a0, 0 + + a1, . )
= (a0, a1, a2, . ) = f = f + 0, deci 0 este element neutru pentru adunare. Daca
fIA', f = (a0, a1, a2, . ), atunci -f = (- a0, -
a1, - a2, . ) este opusul lui f si f + (-
f) = (- f) + f = 0 .
Inmultirea pe A se defineste
astfel:
F g =
(a0b0, a0b1 + a1b0, a0b2 + a1b1 + a2b1, . ) = (c0, c1, . ) , unde Ck=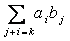
Este clar ca f, gIA'. Inmultirea pe A', astfel
definita , este asociativa, comutativa si are element
unitate. Sa aratam mai intai
asociativitatea .
Fie f, g, h IA' , unde f = (a0, a1, a2, . ) , g =
(b0, b1, b2, . ) , h = (c0, c1, ,c2, . ) si sa aratam ca
(fg)h = f(gh).
Fie fg = (d0, d1, d2, . ). Atunci 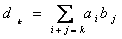 . De asemenea, fie
. De asemenea, fie
(fg)h = (d0',d1',d2', . ), unde d'm =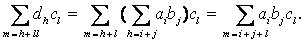
Daca gh = (c0,c1, . ), atunci :
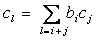 si fie f(gh) = (l'0,l'1,l'2, . ), unde :
si fie f(gh) = (l'0,l'1,l'2, . ), unde :
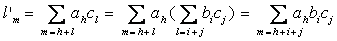
Deci d'm = l'm pentru orice m. Deci (fg)h = f(gh) .
Comutativitatea inmultirii rezulta din faptul ca inmultirea in inelul
A este comutativa, iar in expresia produsului polinoamelor f si g termenii factorilor intervin in mod simetric.
Elementul unitate din A' este sirul (1, 0, 0, . ) . Inmultirea
pe A' este distributiva fata de adunare. Intr-adevar, cu
notatiile de mai sus, rezulta :
f(g + h) = (d0, d1, . ) , unde 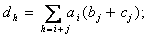
fg + fh = (d'0,d'1, . ), unde 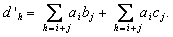
Cum operatia de inmultire pe A este distributiva fata de
adunare rezulta f(g + h) = fg + fh.
Evident are loc si relatia (f + g)h
= fh + gh si afirmatia s-a demonstrat.
Propozitia 5.1.
Daca A este un inel unitar comutativ, atunci multimea A' ( a
sirurilor de elemente din A, care au numai un numar finit de termeni
nenuli) impreuna cu operatiile de adunare si inmultire definite mai
sus este un inel comutativ si unitar.
Elementele acestui inel se numesc polinoame
peste A sau polinoame cu coeficienti din A .
Daca f = (a0, a1, . ) este un polinom nenul
(adica nu toti termenii ai sunt nuli ) si daca n este cel mai
mare numar natural cu proprietatea ca an 0 , atunci n se numeste gradul
polinomului f . Pentru polinomul nul nu se defineste gradul. Convenim sa consideram gradul sau ca fiind
- . Daca gradul (f) = n , atunci a0,
a1, . , an se numesc coeficientii polinomului f.
Fie aplicatia u: A A' definita prin u(a) = (a, 0, 0, . )
. Aplicatia u este injectiva , caci, daca u(a) = u(b), atunci (a, 0,
. ) = (b, 0, . ) a = b. De asemenea , u(a + b) = u(a) + u(b) si u(ab) =
u(a)u(b) , a, b I A , deoarece , dupa definitie
, este evident ca (a, 0, . ) + (b, 0, . ) = (a + b, 0, . ) si (a, 0, . ) (b, 0, . ) = (ab, 0, . ) .
Deci
u este omomorfism injectiv. Acest fapt permite sa se identifice elementul a IA cu
imaginea sa prin u , adica polinomul (a, 0, . ) din A'. Astfel, A se poate considera ca un subinel al lui A'.
Notam prin X polinomul (0, 1, 0, . ), care se numeste nedeterminata X.
Obtinem:
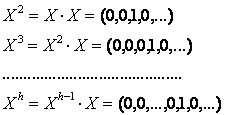
Pentru orice a I A, avem ax = (0, 0, . , 0, a, 0, . ). Fie acum un
polinom de gradul n , f = (a0, a1, a2, . , an, 0, . ) = (a0, 0, 0, . ) + (0, a1,
0, . ) + .
= (0, 0, . , 0, a, 0, . ). Fie acum un
polinom de gradul n , f = (a0, a1, a2, . , an, 0, . ) = (a0, 0, 0, . ) + (0, a1,
0, . ) + .
. + (0, 0, . an, 0, . ) = a0(1, 0, . ) + a1(0, 1,
0, . ) + . + an(0, 0, . , 1, 0, . ) = 
Daca an = 1 , spunem ca polinomul este
unitar. Inelul A' obtinut se numeste inelul polinoamelor in
nedeterminata X cu coeficienti in inelul A (sau peste inelul A) si se
noteaza cu A[X]. Observam ca f are gradul 0 sau - daca si numai daca f apartine inelului A. Din
definitia sumei si produsului a doua polinoame , rezulta ca
grad (f + g) max
(grad(f), grad(g)) ; grad(fg) grad(f) + grad(g), pentru f, g IA[x].
Daca A este un domeniu de integritate
, se poate inlocui a doua inegalitate printr-o egalitate.
Propozitia 5.2.
Daca A este un domeniu de integritate, atunci
inelul de polinoame A[x] este domeniu de integritate.
Demonstratie:
Fie f,
gIA[x] ; 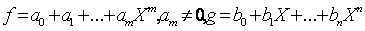
Atunci :
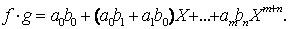
A fiind domeniu de integritate, rezulta
din am 0 si bn 0 ca ambn 0, adica fg 0. In
particular , pentru un corp comutativ K, inelul polinoamelor de o
nedeterminata cu coeficienti in K este un inel integru.
Propozitia 5.3.
Fie A un domeniu de integritate si A[x] inelul polinoamelor in
nedeterminata X cu coeficienti in A. Atunci elementele inversabile ale
inelului A[x] coincid cu elementele inversabile ale inelului A. deci, cu
notatiile cunoscute, avem: u(A[x]) ==u(A).
Demonstratie:
Fie aIA, inversabil in A , adica
exista bIA a.i. a b = 1. Evident, aceasta relatie are loc si in A[x] , deoarece a si b sunt
polinoame de gradul zero, deci a este inversabil in A[x].
Invers, fie f un polinom din A[x] inversabil.
Atunci exista un polinom g I
A[x] a.i. fg = 1 si , deci, grad(f) + grad(g) =
grad(1) = 0, adica f, g I A.
Deci f I A si f este inversabil in A. In
particular, pentru un corp comutativ K, polinoamele inversabile din K[x] sunt
polinoame de gradul 0 si numai acesta. Daca A nu este domeniu de integritate, putem avea u(A[x]) u(A).
Intr-adevar , polinomul neconstant 1 + 2X I Z [x] este inversabil, deoarece (1+2x)(1+2x) = 1.
Exemple . ( Probleme )
1. Sa se arate ca
in inelul Q[x, y], polinomul x + y este
ireductibil.
Solutie.
Este clar ca x + y este nenul si
neinversabil . Daca ar fi reductibil s-ar descompune astfel: x + y = (a + a x + a y)(b + b x + b y) = a b
+ (a b + a b )x + + (a b + a b
)y + (a b + a b )xy + a b x + a b y . De aici obtinem a b = 0, a b = 1 ,
a b = 1, a b + a b = 0 de unde a = b = 0.
Apoi, din a a (a b + a b ) = 0 se obtine se obtine ca a + a = 0,
contradictie .
2. Sa
se arate ca in inelul C[X, Y] , polinomul X (Y + 1) + X Y + X Y + + XY + Y este ireductibil, n 2 , n I N .
Solutie .
Polinomul poate fi considerat in nedeterminata X cu coeficienti in
Q[Y] deci, in inelul Q[X][Y]. Atunci, pentru valoarea particulara y = p, p -
prim , in inelul factorial Q[Y] sunt indeplinite conditiile din criteriul
lui Eisenstein . Deci, polinomul X (Y+1) +X Y +X Y +XY +Y este ireductibil in
inelul Q[X][Y] = Q[X,Y] .
3. Sa
se arate ca polinomul f = 3X + 4X - 6X + 7X + 21 este ireductibil in Z[X] .
Solutie .
Polinomul f este primitiv. Aplicam criteriul reductiei pentru p=2.
Avem f = X +X +1I Z [X] si aratam ca
f este ireductibil in Z [X]. Deoarece
f(0) = (1) = 1 0 , rezulta ca f nu are
factori de gradul intai in descompunere. Fie acum X +X +1= (aX + bX + c)(mX +
nx + pX + q). Prin identificarea coeficientilor se ajunge la am = 1, an +
mb = 0, ap + bn + cm = 0, aq + bp + cn = 1, cq = 1. De aici, avem a = m = c = q
= 1 si deci, b + n = 0, p + bn = 1, bp + n = 1, b + p = 0, de unde, prin calcul
simplu ajungem la a = 1, contradictie. In concluzie, f este ireductibil in
Z [X]. Din criteriul reductiei rezulta f ireductibil in Z[X].
6. Inelul claselor de resturi modulo n
Operatiile de
adunare si inmultire confera multimii Z a numerelor intregi
o structura de inel comutativ unitar si fara divizori ai lui zero .(pe scurt inel integru
) .In acest inel multimea nZ a multiplilor numarului natural n
(fixat) formeaza un ideal (bilateral) . Pe de alta parte daca I
este un ideal al inelului (Z, +, ) atunci I este un subgrup al
grupului (Z, +) deci exista un numar natural n astfel incat I = nZ .
Daca I = nZ si J = mZ sunt
doua ideale ale lui Z atunci I + J este de asemenea un ideal al lui Z
si exista d I Z astfel incat I + J = dZ sau nZ +
mZ = dZ (putem presupune d I N) . Din relatia n m I dZ
rezulta d n si d m , iar din relatia d I nZ + mZ
rezulta ca exista a, b I Z astfel incat d = an + bm . Din
urma relatiei deducem ca orice divizor comun al lui m si n este
si un divizor al lui d . Prin urmare d este cel mai mare divizor comun al
numerelor intregi n si m . Analog
se demonstreaza ca daca nZ mZ = qZ atunci q este cel mai mic
multiplu comun al lui n si m . De asemenea are loc relatia (nZ)(mZ) = (nm)Z .
Inelele factor ale
inelului Z se construiesc prin factorizare cu ideale care au forma nZ , n I N .
Reamintim ca pornind de la structura de grup aditiv a lui Z si
considerand un subgrup nZ al acestuia , relatia
x y x - y I nZ
este o relatie de echivalenta (numita si
relatie de congruenta modulo n ) si notata in teoria
numerelor prin x s z (mod n) ale carei clase de
echivalenta au forma
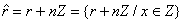
Clasele de
echivalenta se mai numesc si clase de resturi modulo n , in
rolul reprezentantului r putand fi ales totdeauna un numar natural cuprins
intre 0 si n - 1 . Multimea acestor clase Zn = capata o structura de grup comutativ in raport cu
operatia 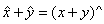 Constructia amintita tine
seama numai de operatia de adunare pe Z . Tinand
cont si de operatia de inmultire din Z , deci de structura de
inel , se poate completa si structura lui Zn . Astfel operatia
Constructia amintita tine
seama numai de operatia de adunare pe Z . Tinand
cont si de operatia de inmultire din Z , deci de structura de
inel , se poate completa si structura lui Zn . Astfel operatia
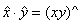
impreuna cu operatia de adunare induc pe Zn o structura
de inel comutativ si unitar Acest inel poarta numele de inelul
claselor de resturi modulo n . Elementele remarcabile ale acestui inel sunt
urmatoarele : 0 - elementul neutru (al operatiei de adunare ) , 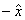 - opusul clasei
- opusul clasei 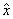 ,
, 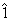 - elementul unitate (al
operatiei de inmultire ) .
- elementul unitate (al
operatiei de inmultire ) .
Aplicatia jn : Z Zn definita prin jn (x) = 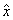 este un morfism unitar de inele deoarece :
este un morfism unitar de inele deoarece :

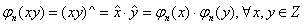
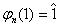
Morfismul jn se
numeste surjectia canonica a lui Z pe inelul sau factor Zn . Daca n = 0 atunci fiecare clasa de
resturi in Z0 este de forma 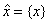 . Surjectia canonica j0 = Z Z0 este
si injectiva , deci inelele Z si Z0 sunt canonic izomorfe .
. Surjectia canonica j0 = Z Z0 este
si injectiva , deci inelele Z si Z0 sunt canonic izomorfe .
Daca n = 1 atunci  = Z , deci toate numerele intregi fac parte
dintr-o singura clasa de resturi , iar inelul Z1 este inelul nul , Z1
=
= Z , deci toate numerele intregi fac parte
dintr-o singura clasa de resturi , iar inelul Z1 este inelul nul , Z1
= 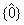 .
.
Inelul Zn are mai multe aplicatii in teoria numerelor . In
continuare , pe baza proprietatilor grupurilor finite vom deduce
cateva astfel de rezultate . Pentru aceasta vom stabilii mai intai care sunt
unitatile (elementele inversabile ) inelului Zn .
Teorema
6.1. In inelul Zn , n > 1, elementul 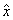 este inversabil daca si numai
daca x si n sunt relativ prime .
este inversabil daca si numai
daca x si n sunt relativ prime .
Demonstratie. Observam mai intai ca daca x
si n sunt relativ prime si y =
x + kn , k I Zn , atunci z si n sunt de asemenea
relativ prime. Daca 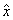 este inversabila in Z n atunci
exista
este inversabila in Z n atunci
exista 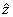 I Z n
astfel incat
I Z n
astfel incat 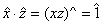 , de unde xz = 1 + kn , pentru un anumit k I Z . Din
relatia
, de unde xz = 1 + kn , pentru un anumit k I Z . Din
relatia
xz - kn = 1
rezulta ca divizorii comuni ai lui x si n sunt 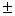 1 , deci x si n sunt relativ prime .
Reciproc , daca x si n sunt relativ prime , atunci exista
numerele intregi a si b astfel incat ax + bn = 1 .Luand imaginile acestor
elemente prin surjectia canonica jn si tinand seama ca jn (n) =
0 rezulta
1 , deci x si n sunt relativ prime .
Reciproc , daca x si n sunt relativ prime , atunci exista
numerele intregi a si b astfel incat ax + bn = 1 .Luand imaginile acestor
elemente prin surjectia canonica jn si tinand seama ca jn (n) =
0 rezulta 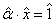 , adica
, adica 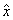 este inversabila in Zn .
este inversabila in Zn .
Conform teoremei precedente , de
exemplu , in Z15 , 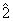 si
si  sunt inversabile , dar
sunt inversabile , dar 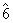 nu este inversabila .
nu este inversabila .
Consecinta . Daca n este numar prim , atunci Zn este corp .
Intr-adevar daca n este numar prim , atunci 1, 2, . . n - 1 sunt relativ prime cu n si deci toate
elementele inelului Zn diferite de elementul neutru al adunarii (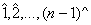 ) sunt inversabile .
) sunt inversabile .
2. Consecinta . Inelul Zn (n > 1)
contine atatea elemente inversabile cate numere naturale mai mici ca n
si prime cu n exista ,
adica j (n) elemente , unde j : N N este functia lui Euler .
3. Observatie . Legatura dintre elementele inversabile din Zn si j (n) ne
permite sa dam o noua demonstratie faptului ca
indicatorul lui Euler este o functie multiplicativa . Pentru aceasta
vom demonstra lema care urmeaza .
1. Lema . Daca m1 si m2 , sunt numere
intregi relativ prime , atunci 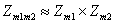 .
.
Demonstratie .
Consideram functia f : Z Zm1 x Zm2 , definita prin f (x)
= (j1(x ) , j2 (x)) , unde j j2 sunt surjectiile canonice ale
lui Z pe Zm1 , Zm2 . Se verifica imediat ca f este morfism de inele .
Daca x I Ker f , atunci m1 x , m2 x , si deoarece m1 , m2 sunt
relativ prime , deducem m1m2 x . Daca m1m2 x ,
atunci x I Ker f . Deci Ker f = m1m2 Z . Conform teoremei
fundamentale de izomorfism Im f Z Ker f =
Zm1m2 . Deoarece Im f are
m1m2 elemente rezulta ca Im f
= Zm1 x Zm2 , de unde izomorfismul din enunt .
Aplicand propozitiile din 5. pentru izomorfismul din lema precedenta
se obtine U(Zm1m2) u (Zm1) x U (Zm2) din care deducem
ca j( m1m2 ) = j(m1) j(m2)


