Matematici aplicate in economie 1 - Algebra
liniara - test
MULTIPLE CHOICE
1. Fie urmatoarea forma patratica:
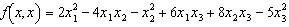
Aflati
matricea asociata acestei forme patratice.
ANS: A
2. Fie urmatoarea forma patratica:
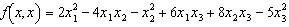
Precizati sirul minorilor asociati
acestei forme patratice
ANS: B
3. Fie urmatoarea forma patratica:
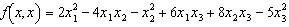
Sa
se aduca la o suma de patrate prin metoda lui Jacobi
ANS: A
4. Fie 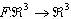 un operator liniar ca re in baza canonica este
dat de matricea :
un operator liniar ca re in baza canonica este
dat de matricea :
 .Precizati
polinomul caracteristic asociat acestui operator.
.Precizati
polinomul caracteristic asociat acestui operator.
ANS: A
5. Fie 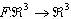 un operator liniar care in baza canonica este
dat de matricea :
un operator liniar care in baza canonica este
dat de matricea :
 .Aflati
valorile proprii asociate acestui operator.
.Aflati
valorile proprii asociate acestui operator.
ANS: B
6. Fie operatorul liniar 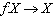 ,
unde
,
unde  .Determinati
spatiul vectorial X
.Determinati
spatiul vectorial X
ANS: B
7. Fie operatorul liniar 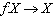 ,
unde
,
unde  .Precizati
matricea asociata acestui operator liniar.
.Precizati
matricea asociata acestui operator liniar.
ANS: C
8. Fie operatorul liniar 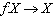 ,
unde
,
unde  .Determinati
polinomul caracteristic asociat acestui operator
.Determinati
polinomul caracteristic asociat acestui operator
ANS: C
9. Fie operatorul liniar 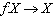 ,
unde
,
unde  .
Aflati valorile proprii asociate pentru acest operator liniar.
.
Aflati valorile proprii asociate pentru acest operator liniar.
ANS: B
Fie operatorul liniar 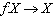 ,
unde
,
unde  .Aflati
vectorii proprii asociati acestui
operator liniar.
.Aflati
vectorii proprii asociati acestui
operator liniar.
ANS: D
Aflati coordonatele vectorului x=(1,1,1), 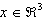 in baza canonica din spatiul
in baza canonica din spatiul 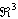
ANS: A
Aflati coordonatele vectorului x=(1,1,1), 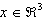 in baza
in baza
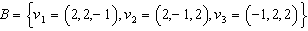 din spatiul
din spatiul 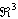
ANS: B
Aplicand metoda Gauss Jordan la un
moment dat s-a obtinut :
A I
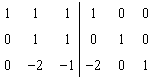
Detrminati 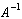 pornind calculele de la schema data
pornind calculele de la schema data
ANS: A
14. Se da forma biliniara urmatoare:

Scrieti matricea asociata
ANS: A
15. Se da matricea: 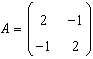 atasata
unei forme biliniare. Scrieti forma biliniara corespunzatoare.
atasata
unei forme biliniare. Scrieti forma biliniara corespunzatoare.
ANS: A
16. Se da forma patratica 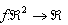
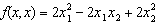
Se se reduca la forma canonica
utilizand metoda lui Jacobi
ANS: A
17. Se da forma patratica 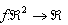
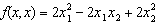
Sa
se calculeze minorii matricei asociate acestei forme patratice.
ANS: B
18. Sa se reduca la forma canonica forma
patratica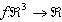
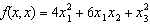
Scrieti minorii asociati acestei
forme patratice
ANS: C
19. Sa se reduca la forma canonica
urmatoarea forma patratica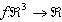
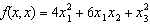
(Utilizand metoda lui Jacobi)
ANS: C
20. Fie urmatorul operator
:
 ,
, 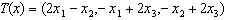
Precizati
pe ce spatiu X se lucreaza
ANS: C
21. Sa se scrie matricea operatorului :
 ,
, 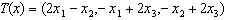
ANS: B
22. Sa se determine suma valorilor proprii
pentru urmatorul operator
T:X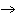 X
determinat prin matricea sa in baza canonica
X
determinat prin matricea sa in baza canonica
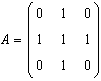
ANS: C
23. Pentru urmatorul operator
T:X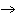 X
determinat prin matricea sa in baza canonica
X
determinat prin matricea sa in baza canonica 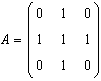
stabiliti care este ecuatia caracteristica
ANS: A
24. Pentru urmatorul operator
T:X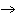 X
determinat prin matricea sa in baza canonica
X
determinat prin matricea sa in baza canonica 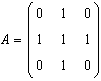 aflati vectorii proprii asociati.
aflati vectorii proprii asociati.
|
a.
|
a(1,1,-1),b(-1,-1,-1),c(1,1,1), a,b,c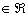
|
c.
|
a(1,0,-1),b(-1,1,-1),c(1,2,1), a,b,c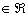
|
|
b.
|
a(1,0,-1),b(1,1,1),c(2,2,1), a,b,c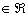
|
d.
|
a(2,0,-1),b(-1,1,-1),c(2,2,1), a,b,c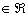
|
ANS: C
25. Scrieti ecuatia caracteristica pentru
operatorul T:X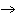 X
dat prin matricea sa in baza canonica:
X
dat prin matricea sa in baza canonica:
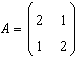
ANS: B
26. Fie operatorul T:X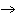 X
dat prin matricea sa in baza canonica:
X
dat prin matricea sa in baza canonica:
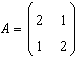
Aflati produsul valorilor proprii
asociate acestui operator
ANS: A
27. Fie operatorul T:X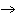 X
dat prin matricea sa in baza canonica:
X
dat prin matricea sa in baza canonica:
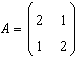
Stabiliti care sunt vectorii
proprii asociati acestui operator:
|
a.
|
(a,a),(b,b), 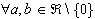
|
c.
|
(a,a),(b,b), 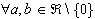
|
|
b.
|
(a,-a),(b,b), 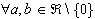
|
d.
|
(a,-a),(b,2b), 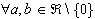
|
ANS: B
28. Fie matricea  .
Scrieti forma biliniara corespunzatoare:
.
Scrieti forma biliniara corespunzatoare:
ANS: B
29. Fie vectorii v1, v2
I R2 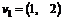 si
si 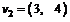 Sa se scrie vectorul
Sa se scrie vectorul 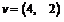 ca o combinatie liniara a valorilor v1,
v2.
ca o combinatie liniara a valorilor v1,
v2.
ANS: A
30. Fie A = unde 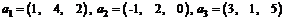
Sa se scrie
vectorul 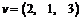 ca o combinatie liniara in baza A =
ca o combinatie liniara in baza A =
ANS: B
31. Fie vectorii v1, v2
I R2 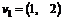 si
si 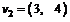 Sa se scrie vectorul
Sa se scrie vectorul 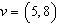 ca o combinatie liniara a valorilor v1,
v2.
ca o combinatie liniara a valorilor v1,
v2.
ANS: A
32. Fie vectorii 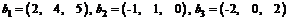 si B = baza in R3 . Sa se
exprime vectorul
si B = baza in R3 . Sa se
exprime vectorul 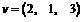 ca o combinatie liniara in baza B =
ca o combinatie liniara in baza B =
ANS: C
33. Fie V
spatiu vectorial n - dimensional peste corpul de scalari K si T : V V o aplicatie liniara. Un scalar l I K se numeste pentru
aplicatie liniara T daca exista cel putin un vector
nenul v I V astfel incat:
T(v) = lv.
|
a.
|
valoare proprie
|
c.
|
valoare
caracteristica
|
|
b.
|
vector propriu
|
d.
|
alt raspuns.
|
ANS: A
34. Vectorul nenul v I V care verifica relatia T(v) = lv se numeste pentru aplicatia T
asociata valorii proprii l
|
a.
|
valoare
proprie
|
c.
|
valoare
caracteristica
|
|
b.
|
vector propriu
|
d.
|
alt
raspuns
|
ANS: B
35. Polinomul P(l) = det (AT - lEn) se
numeste asociat aplicatiei liniare T ecuatia P(l) = 0 se numeste ecuatia
caracteristica a aplicatiei T.
|
a.
|
valoare
proprie
|
c.
|
valoare caracteristica;
|
|
b.
|
polinom
caracteristic
|
d.
|
alt raspuns
|
ANS: B
36. Ecuatia
det (AT - l En)=0 se
numeste a aplicatiei T.
|
a.
|
ecuatie
caracteristica
|
c.
|
valoare
caracteristica
|
|
b.
|
polinom
caracteristic
|
d.
|
alt
raspuns
|
ANS: A
37. Scrieti matricea asociata
operatorului liniar dat de 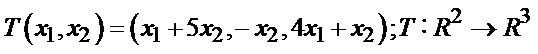
ANS: C
38. Scrieti matricea asociata
operatorului liniar dat de 
ANS: A
39. Aduceti
la forma canonica forma patratica urmatoare 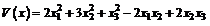 , utilizati metoda lui Jacobi.
, utilizati metoda lui Jacobi.
ANS: B
40. Determinati
a, 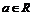 astfel incat forma
patratica urmatoare sa fie pozitiv definita
astfel incat forma
patratica urmatoare sa fie pozitiv definita 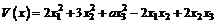
ANS: A
41. Determinati
valorile proprii ale operatorului liniar 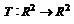 avand matricea
atasata
avand matricea
atasata 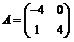
ANS: C
42. Determinati
vectorii proprii corespunzatori operatorului liniar 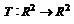 avand matricea
atasata
avand matricea
atasata 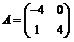
ANS: A
43. Fie vectorii din spatiul R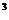 : v
: v = ( 1, 4, 2 ); v
= ( 1, 4, 2 ); v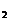 = ( -1, 2, 0 );
= ( -1, 2, 0 ); 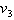 = ( 3, 2, 5 ).
Stabiliti daca
= ( 3, 2, 5 ).
Stabiliti daca
|
a.
|
vectorii sunt liniari dependenti
|
c.
|
vectorii sunt
liniari independenti
|
|
b.
|
multimea B = 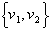 formeaza o baza a spatiului R formeaza o baza a spatiului R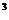
|
d.
|
alt raspuns
|
ANS: C
44. Sa se
exprime vectorul v = ( 2, 1, 3 ) ca o
combinatie liniara in baza B = 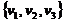
v = ( 1, 4, 2 ) ; v
= ( 1, 4, 2 ) ; v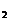 =
(-1, 2, 0 ); v
=
(-1, 2, 0 ); v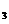 =
( 3, 2, 5 )
=
( 3, 2, 5 )
ANS: B
45. Stabiliti natura formei patratice
urmatoare
g(x)= 8x - 6x
- 6x x
x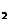 + 2x
+ 2x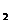 x
x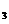 + 4x
+ 4x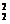 +
+ 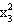
|
a.
|
pozitiv definita
|
c.
|
semipozitiv definita
|
|
b.
|
negativ definita
|
d.
|
nedefinita
|
ANS: A
46. Valorile proprii ale operatorului liniar
T: R³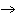 R³,
R³,
T(v) = ( 4v - v
- v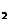 + v
+ v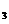 ,
v
,
v + 3v
+ 3v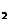 -
v
-
v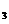 ,
v
,
v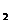 + v
+ v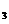 )
sunt:
)
sunt:
ANS: B
47. Radacinile
ecuatiei caracteristice asociate unei aplicatii liniare se numesc :
|
a.
|
valori proprii
|
c.
|
vectori proprii
|
|
b.
|
puncte de
extrem local
|
d.
|
vectori liniar
independenti
|
ANS: A
48. Matricea asociata unei forme patratice:
|
a.
|
are
determinantul zero
|
c.
|
are rangul 3
|
|
b.
|
este simetrica
|
d.
|
are
determinantul diferit de zero
|
ANS: B
49. Daca intr-o
forma patratica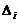 > 0 pentru i par, si
> 0 pentru i par, si 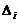 < 0 pentru i impar, atunci forma patratica este:
< 0 pentru i impar, atunci forma patratica este:
|
a.
|
nedefinita
|
c.
|
seminegativ
definita
|
|
b.
|
negativ
definita
|
d.
|
pozitiv
definita
|
ANS: B
50. Sa se
rezolve cu metoda eliminarii (pivotului) sistemul:
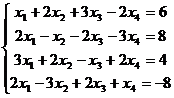
|
a.
|
sistemul este
incompatibil
|
c.
|
x =
-1; x =
-1; x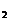 =
2; x =
2; x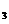 =
-1; x =
-1; x =
-2 =
-2
|
|
b.
|
x =
1; x =
1; x =
2; x =
2; x =
-1; x =
-1; x =
-2 =
-2
|
d.
|
sistemul este compatibil simplu nedeterminat
|
ANS: B
51. ) este combinatie liniara de (1,1) si (1,0) pentru ca
|
a.
|
pentru orice
numere reale a,b avem ca (1,2)=a(1,1)+b(1,0)
|
|
b.
|
exista numere
reale a,b asa ca (1,2)=a(1,1)+b(1,0)
|
|
c.
|
daca (1,2)=a(1,1)+b(1,0) atunci a=b =0
|
|
d.
|
nu exista numere reale a,b asa
ca (1,2)=a(1,1)+b(1,0)
|
ANS: B
52. ) si (1,0) formeaza un sistem liniar independent pentru ca
|
a.
|
pentru orice
numere reale a,b avem ca (0,0)=a(1,1)+b(1,0)
|
|
b.
|
exista numere
reale a,b asa ca (0,0)=a(1,1)+b(1,0)
|
|
c.
|
daca
(0,0)=a(1,1)+b(1,0) pentru doua numere reale a,b atunci a=b=0
|
|
d.
|
nu exista numere reale a,b asa
ca (0,0)=a(1,1)+b(1,0)
|
ANS: C
53. Cat este
2(1,1)+3(0,1)?
ANS: C
54. Se
considera transformarea liniara
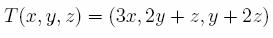
Care din
urmatoarele matrici este matricea lui 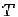 in baza canonica a lui
in baza canonica a lui 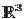
ANS: B
55. Se
considera transformarea liniara

Valorile proprii ale transformarii 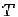 sunt
sunt
ANS: D
56. Se
considera transformarea liniara
T(x,y,z)=(3x,3y+z,y+3z)
Valorile proprii ale transformarii 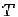 sunt
sunt
ANS: D
57. Se
considera transformarea liniara 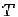 a
carei matrice asociata in baza canonica este
a
carei matrice asociata in baza canonica este
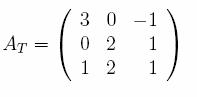
Atunci 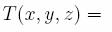
ANS: B
58. Se
considera forma patratica
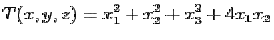
Forma
canonica a acestei forme patratice este
ANS: A
59. Se
considera forma patratica
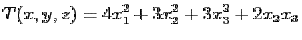
Forma canonica
a acestei forme patratice obtinuta cu metoda lui Jacobi este
ANS: D
60. Se da urmatoarea forma patratica 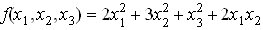 .
Matricea ei in baza canonica a lui
.
Matricea ei in baza canonica a lui  este
este
ANS: B
61. Se considera functia 
Aceasta
functie nu este o transformare liniara pentru ca exista termenul
ANS: B
62. Se considera functia 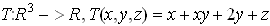
Aceasta
functie nu este o transformare liniara pentru ca exista termenul
ANS: B
63. Valorile proprii ale matricii 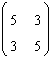 sunt
sunt
ANS: C
64. Se da urmatoarea forma patratica 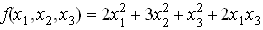 .
Matricea ei in baza canonica a lui
.
Matricea ei in baza canonica a lui  este
este
ANS: B
65. Se da urmatoarea forma patratica 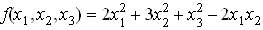 .
Matricea ei in baza canonica a lui
.
Matricea ei in baza canonica a lui  este
este
ANS: B
66. Valorile proprii ale matricii 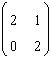 sunt
sunt
ANS: B
67. Se da transformarea liniara
T(x,y)=(2x+y,x-5y). Matricea asociata acestei transformari liniare in baza
canonica a lui  este
este
ANS: C
68. Se da o transformare liniara a carei
matrice asociata in baza canonica este
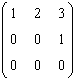 . Atunci valorile propriii ale
transformarii liniare sunt
. Atunci valorile propriii ale
transformarii liniare sunt
ANS: C
69. Se da o transformare liniara a carei
matrice asociata in baza canonica este
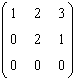 . Atunci valorile propriii ale
transformarii liniare sunt
. Atunci valorile propriii ale
transformarii liniare sunt
ANS: C
70. Se da o transformare liniara a carei
matrice asociata in baza canonica este
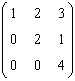 . Atunci valorile propriii ale
transformarii liniare sunt
. Atunci valorile propriii ale
transformarii liniare sunt
ANS: C
71. Matricea asociata unei transformari in
baza canonica este 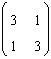 .
Atunci polinomul caracteristic al acestei transformari este
.
Atunci polinomul caracteristic al acestei transformari este
ANS: A
72. Matricea asociata unei transformari in
baza canonica este  .
Atunci polinomul caracteristic al acestei transformari este
.
Atunci polinomul caracteristic al acestei transformari este
ANS: B
73. Matricea asociata unei transformari in
baza canonica este  .
Atunci polinomul caracteristic al acestei transformari este
.
Atunci polinomul caracteristic al acestei transformari este
ANS: B
74. Matricea asociata unei transformari in
baza canonica este 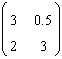 .
Atunci polinomul caracteristic al acestei transformari este
.
Atunci polinomul caracteristic al acestei transformari este
ANS: C
75. Matricea asociata unei transformari in
baza canonica este 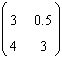 Atunci polinomul caracteristic al
acestei transformari este
Atunci polinomul caracteristic al
acestei transformari este
ANS: A
76. Fie urmatoarea forma patratica:
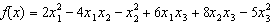
Precizati
sirul minorilor asociati acestei forme patratice(metoda lui Jacobi)
ANS: B
77. Fie urmatoarea forma patratica:
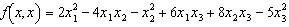
Sa
se aduca la o suma de patrate prin metoda lui Jacobi
ANS: A


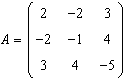
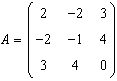
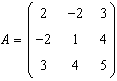
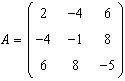


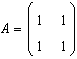
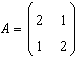
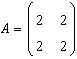
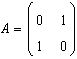
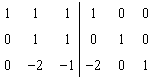
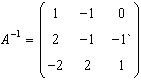

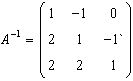
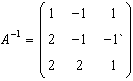

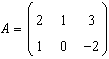

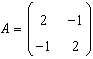
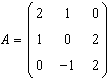
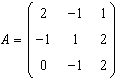
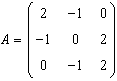
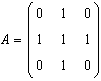
 .
Scrieti forma biliniara corespunzatoare:
.
Scrieti forma biliniara corespunzatoare: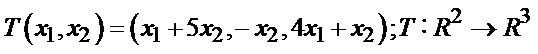
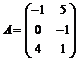
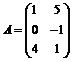
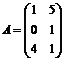




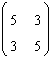 sunt
sunt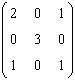
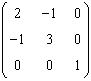
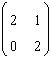 sunt
sunt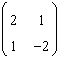
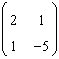
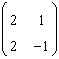
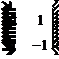
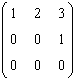
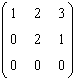
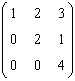
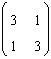 .
Atunci polinomul caracteristic al acestei transformari
.
Atunci polinomul caracteristic al acestei transformari  .
Atunci polinomul caracteristic al acestei transformari
.
Atunci polinomul caracteristic al acestei transformari  .
Atunci polinomul caracteristic al acestei transformari
.
Atunci polinomul caracteristic al acestei transformari 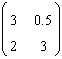 .
Atunci polinomul caracteristic al acestei transformari
.
Atunci polinomul caracteristic al acestei transformari