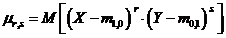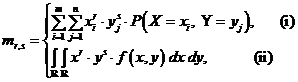Momentele variabilelor aleatoare vectoriale
Fie 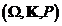 un
camp (borelian) de probabilitate. Vom considera
un
camp (borelian) de probabilitate. Vom considera  o variabila aleatoare bidimensionala.
o variabila aleatoare bidimensionala.
Definitia
2. Valoarea medie a
produsului  se
numeste moment initial de ordinul r in raport cu componenta X
si de ordinul s in raport cu componenta Y a variabilei
aleatoare vectoriale (X,Y),
se
numeste moment initial de ordinul r in raport cu componenta X
si de ordinul s in raport cu componenta Y a variabilei
aleatoare vectoriale (X,Y),  , notat mr,s.
, notat mr,s.
Conform acestei definitii avem: 
mr,s se poate exprima sub forma:
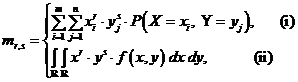
dupa
cum (X,Y) este variabila aleatoare discreta i) sau
continua ii).
De aici pentru 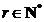 si
si 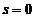 , obtinem:
, obtinem:

iar pentru
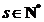 si
si 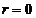 avem:
avem:

adica
momentul initial de ordinul r al componentei X (mr,0)
si momentul initial de ordinul s al componentei Y (m0,s).
Pentru 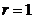 si
si 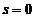 se
obtine media componentei X, iar pentru
se
obtine media componentei X, iar pentru 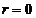 si
si  se
obtine media componentei Y:
se
obtine media componentei Y:
i) 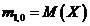 ii)
ii) 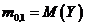
Daca m1,0 si m0,1
sunt finite definim variabila aleatoare vectoriala:
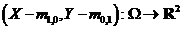
Definitia 3. Numim moment centrat al variabilei aleatoare (X,Y),
de ordinul r in raport cu componenta X si de ordinul s
in raport cu componenta Y, media produsului 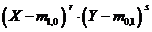 , notat
, notat 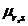
Prin urmare avem: