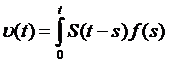Problema
Cauchy abstracta
1 Solutii clasice si moderate.
Proprietati
Fie X un spatiu Banach
real sau complex , S = 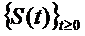 un C
un C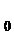 - semigrup si
- semigrup si
A : D(A) 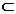 X
X 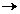 X generatorul sau infinitezimal.
X generatorul sau infinitezimal.
Pentru fiecare 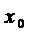
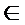
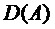 problema Cauchy
omogena
problema Cauchy
omogena
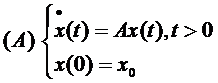
are o
unica solutie
x(t) = S(t)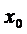
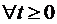 .
.
In
continuare studiem problema Cauchy neomogena descrisa de sistemul
(S) 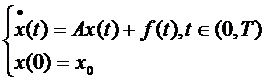
unde T 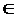 ( 0,
( 0,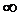 ], f : [ 0,T )
], f : [ 0,T ) 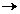 X ,
X , 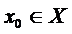 .
.
Definitia 1.1. O functie x : [0,T ) 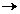 X se
numeste solutie clasica pentru sistemul (S) daca
indeplineste urmatoarele conditii :
X se
numeste solutie clasica pentru sistemul (S) daca
indeplineste urmatoarele conditii :
(i) x este continua pe [ 0, T) si de clasa 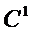 pe ( 0,
T);
pe ( 0,
T);
(ii) x(t) 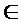 D(A) , pentru orice
D(A) , pentru orice 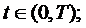
(iii) x verifica sistemul (S).
Teorema 1.1. Daca x este solutie pentru sistemul (S), atunci
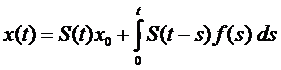
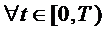 .
.
Definitia 1.3. Fie 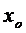
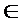 X si f
X si f 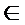
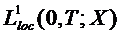 . Functia x : [0,T)
. Functia x : [0,T) 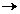 X data de relatia
X data de relatia
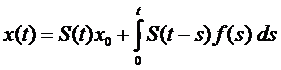 ,
, 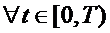
se
numeste solutie moderata (mild) a sistemului (S).
Teorema urmatoare ne da o proprietate importanta a
solutiei moderate.
Teorema 1.2. Daca x : [0,T) 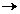 X
este solutia moderata a sistemului (S)
atunci x este continua pe [0,T
X
este solutia moderata a sistemului (S)
atunci x este continua pe [0,T
2 Conditii necesare ca o solutie moderata sa fie
clasica.
Exemplul 2.1. Fie 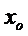
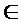
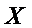 cu proprietatea ca
cu proprietatea ca
S(t)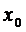
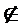 D(A) , pentru orice
D(A) , pentru orice 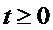 . Consideram sistemul
. Consideram sistemul
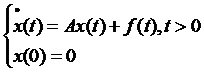
unde f(t) = S(t)x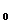 , pentru orice t > 0. Atunci avem ca f este continua
pe
, pentru orice t > 0. Atunci avem ca f este continua
pe 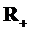 si x(0) =
0
si x(0) =
0 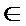 D(A). Cu toate
acestea , solutia moderata are expresia
D(A). Cu toate
acestea , solutia moderata are expresia
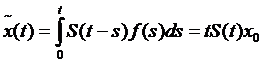 ,
, 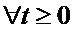 ,
,
deci 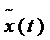
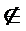 D(A), pentru orice t > 0
D(A), pentru orice t > 0
Teorema
2.2. Fie
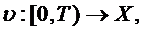
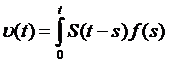 ds .
ds .
Daca x  f este continua pe 0,T) si
f este continua pe 0,T) si 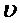 este o aplicatie
de clasa C
este o aplicatie
de clasa C pe (0,T), atunci solutia moderata a sistemului (S) este solutia
clasica.
pe (0,T), atunci solutia moderata a sistemului (S) este solutia
clasica.
Teorema 2.3. Daca x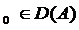 si f este o functie
de clasa
si f este o functie
de clasa 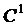 pe 0,T), atunci sistemul (S) are o unica
solutie classica.
pe 0,T), atunci sistemul (S) are o unica
solutie classica.
Bibliografie
1. Buse, C.
- Comportari asimptotice ale proceselor de evolutie, Editura Sedona, Timisoara, 1988;
2. Cristescu, K.
- Analiza functionala, Editura Didactica ;
3. Curtain, R;
Zwart, H. J. - An Introduction to Infinite Dimensional Linear Control Systems
Theory, Springer Verlag , New
York, 1995 ;
4. Curtain, R;
Pritchard, A.J. - Functional Analysis in Modern Applied Mathematics, Mathematics in Science and
Engineering 132, Academic Press 1977;
5. Engel , K. J.;
Nagel, R. - One- Parameter Semigroups for Linear Evolution Equations, Graduate
Texts in Mathematics, vol 194, Berlin 2000;
6. Gaspar,
D.- Analiza functionala, Editura Facla, Timisoara 1981;
7. Hille, E;
Phillips , R. S. - Functional Analysis and Semi-groups American Mathematical
Society, Colloquium Publications Vol 31, Providence, R. I. 1957;
8. Gheorghiu, N.-
Introducere in analiza functionala, Editura Academiei RSR,
Bucuresti 1974;
9. von Neerven,
J. M. A. M.- The Asymptotic Behaviour of
Semigroups of Linear Operators, Operator Theory Advanced and Applications, vol
88, Birkhäuser, Bassel 1996;
10. Pazy, A. -
Semigroups of Linear Operators and Applications to Partial Differential
Equations, Springer Verlag, 1983;
11. Sasu, A. L. .
Sasu, B.- Sisteme liniare cu control, Editura Politehnica Timisoara 2003;
12. Yosida, K-
Functional Analysis, Springer Verlag, 1993.


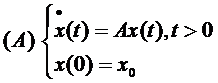
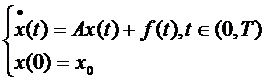
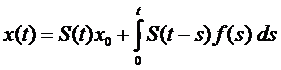
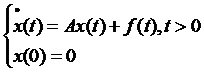
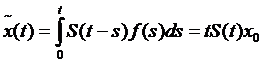 ,
,