Translatia

TRANSLATIA

Cercul

Fie r un numar real, r > 0 si O un punct din plan. Se numeste cerc de centru O si raza r, notat C(O,r), multimea punctelor M din plan pentru care OM = r. Prin raza se mai intelege si un segment OM unde M este pe cerc.

Pozitia unei drepte fata de cerc:

Daca distanta de la centrul unui cerc la o dreapta d este mai mica decat raza cercului atunci dreapta are doua puncte comune cu cercul si se numeste secanta

Daca distanta de la centrul unui cerc la o dreapta d este egala cu raza cercului atunci dreapta are un punct comun cu cercul si se numeste tangenta.

Tangenta este perpendiculara pe raza corespunzatoare. Dintr-un punct exterior cercului se pot duce doua tangente la cerc. Segmentele determinate de punctul exterior si punctele de tangenta sunt congruente.

Daca distanta de la centrul unui cerc la o dreapta d este mai mare decat raza cercului atunci dreapta nu are puncte comune cu cercul si se numeste exterioara.

Unui unghi i se poate circumscrie un cerc (cercul trece prin varfurile triunghiului). Centrul cercului circumscris este intersectia mediatoarelor laturilor triunghiului

Intr-un triunghi se poate inscrie un cerc ( cercul este tangent laturilor triunghiului). Centrul cercului inscris este intersectia bisectoarelor unghiurilor triunghiului.

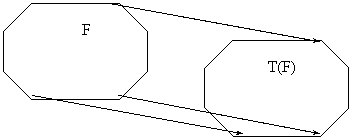
Translatia

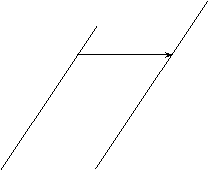
Translatia poate fi sugerata cu ajutorul ideii de miscare sau de deplasare. De exemplu, pentru a trasa o dreapta paralela cu o dreapta data folosind o rigla si un echer se procedeaza astfel: se suprapune una din laturile echerului pste dreapta data, se pune in contact rigla cu cealalta latura a echerului si se deplaseaza astfel incat o latura sa ramana in contact cu rigla. Aceasta deplasare a echerului se numeste translatie si are propietatea ca cealalta latura a sa este tot timpul paralela cu dreapta data. (fig I . )

C C′

A B A` B`

Fig I

Fie, acum, o placa rigida care se deplaseaza pe un plan astfel incat fiecare punct al placii descrie o dreapta. O astfe de deplasare se numeste miscare de translatie.

In figura I. b se considera o placa triunghiulara care are succesiv pozitiile ABC, A'B'C', A''B''C''

C C' C``

B B'

B` `

AA

A A' A``

Comparand pozitia placii ABC cu pozita placii A'B'C' se observa ca vectorii AA', BB', CC', MM' sunt egali.

Se va defini translatia ca o transformare geometrica in care toate punctele unui plan se deplaseaza cu un acelas vector.

Fie v un vector nenul. Se numeste translatia de vector v o functie T prin care fiecarui punct M ii corespunde un punct T(M) = M ' astfel incat MM' = v . Puctul M' se numeste translatul punctului M (fig I.c).

M' = T(M) B' = T(B)

Fig. I.c

A' = T(A)

v C'= T(C)

Daca F este o multime de puncte din plan ( segment, unghi, dreapta, poligon, cerc etc.) se va nota cu T(F) multimea obtinuta prin translarea punctelor multimii F.

Daca se fixeaza un punct O al planului ( de exemplu originea unui reper cartezian) atunci pentru orice pereche de puncte M si M' = T(M) are loc relatia OM' = OM + v.

O translatie este determinata daca se da vectorul v sau daca se cunoaste translatul unui anumit punct adica o pereche M si M' = T(M) atunci v = MM'.

Daca este data o portiune din plan in care este desenat un caroiaj atunci acesta poate fi utilizat pentru a descrie o translatie; in figura I. d v = AA'

Fig .Id

Proprietatile translatiei

Pentru doua puncte distincte A, B adca se noteaza A' = T(A), B' = T(B), atunci AB = A'B' si T(AB) = A'B' (fig. e) (translatia pastreaza lungimea, directia si sensul unui segment orientat).

A' M'

B'

v

Fig. I.e

A

M

B

Daca d este o dreapta atunci T(d) este o dreapta paralela cu ea (fig I.71) ( translatia pastreaza directia dreptlor)

v

Fig.I.71

v

d

Daca F este un poligon atunci T(F) este un poligon congruent cu F ( fig. I.72)

Fig. I.72

v

Daca F este un cerc atunci T(F) este un cerc care are aceeasi raza (I.73).

v

v

Translatia pastreaza directia, sensul, lungimea segmentelor, masura unghiurilor si aria suprafetelor.