Transformata Z si transformata Laplace
discreta
Transformata
Z
Fie  un sir de numere reale
sau complexe.
un sir de numere reale
sau complexe.
Se numeste transformata Z a
sirului  , functia de variabila complexa
, functia de variabila complexa
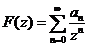 .
.
Daca sirul dat satisface conditia  , unde
, unde 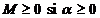 , atunci F(z) defineste o functie olomorfa in
domeniul
, atunci F(z) defineste o functie olomorfa in
domeniul  .
.
Relatia de mai sus, in care este
definit F(z), reprezinta de fapt dezvoltarea acestei functii
intr-o vecinatate a lui  . Astfel, daca F(z) este data, pentru determinarea
sirului
. Astfel, daca F(z) este data, pentru determinarea
sirului  se poate proceda astfel:
se poate proceda astfel:
- se dezvolta F(z) in
jurul lui  , identificandu-se termenii sirului, sau
, identificandu-se termenii sirului, sau
- se aplica formula de calcul pentru
coeficientii dezvoltarii in serie Laurent: 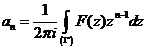 , unde
, unde  este o curba simpla
inchisa cu proprietatea ca in
este o curba simpla
inchisa cu proprietatea ca in 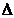 cu
cu  se afla toate
singularitatile lui F(z) aflate la distanta finita.
se afla toate
singularitatile lui F(z) aflate la distanta finita.
Exemplu
pentru determinarea sirului a carui transformata Z se cunoaste
Sa se deduca sirul  daca trasformata sa Z
este
daca trasformata sa Z
este 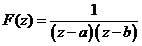 .
.
- Metoda 1):
Dezvoltam F(z) in
jurul lui  :
:
 ,
,
pentru 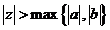 .
.
Rezulta:  .
.
- Metoda 2):
Aplicam formula de calcul a
coeficientilor dezvoltarii in serie Laurent:
 .
.
Conform teoremei reziduurilor:

 ;
;
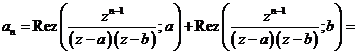
 .
.
Transformata Laplace discreta
Fie 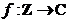 . Daca
. Daca 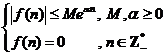 , atunci f se numeste functie original discreta.
, atunci f se numeste functie original discreta.
Se numeste transformata Laplace
discreta a functiei (original discrete) f, functia de variabila
complexa, notata 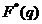 , data de:
, data de:
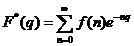 .
.
- Observam ca 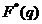 se obtine din F(z)
(transformata Z), luand in definitia acesteia
se obtine din F(z)
(transformata Z), luand in definitia acesteia 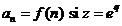 .
.
- De asemenea, se observa ca 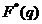 exista pentru
exista pentru 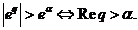
Notatie: legatura
dintre f(n) si 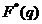 se
noteaza: f(n)
se
noteaza: f(n) 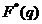 sau
sau 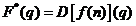 .
.
Are loc formula de inversiune:
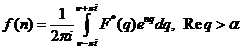 .
.
Exemplu
de calcul si de notatie pentru transformata Laplace
discreta
Sa
calculam transformata Laplace discreta pentru  .
.
Conform
definitiei, 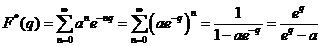 ;
;
(se subintelege ca 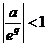 , pentru ca
, pentru ca 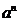 trebuie sa fie functie
original discreta, adica
trebuie sa fie functie
original discreta, adica 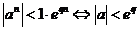 ).
).
Deci, 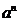
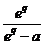 (sau
(sau 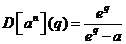 ).
).
Daca  , atunci
, atunci 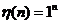
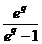 (sau
(sau 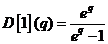 ).
).
Proprietatile transformatei
Laplace discrete si reguli de calcul
- Liniaritatea
Daca 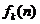
 ,
,  , atunci
, atunci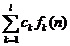
 .
.
- Teorema deplasarii
Daca f(n) 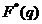 , atunci
, atunci 
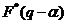 .
.
Exemple pentru
teorema deplasarii si liniaritatea transformatei Laplace
discrete
Sa calculam
transformata Laplace discreta a functiilor 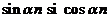 .
.
Folosind
formulele lui Euler, rezulta:
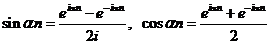 .
.
Din
liniaritate si din teorema deplasarii, avem:
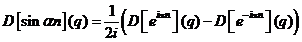 ;
;
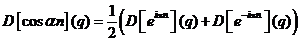 ;
;
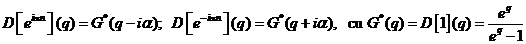 .
.
Prin
urmare:
 ;
;
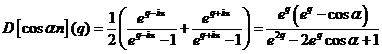 .
.
- Teorema intarzierii
Daca f(n) 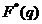 , atunci:
, atunci:
(i) 
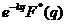 ;
;
(ii) 
 .
.
Exemple pentru
teorema deplasarii si liniaritatea transformatei Laplace
discrete
Sa calculam
transformata Laplace discreta a functiilor 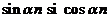 .
.
Folosind formulele
lui Euler, rezulta:
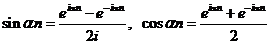 .
.
Din
liniaritate si din teorema deplasarii, avem:
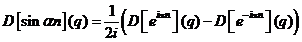 ;
;
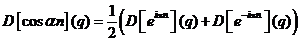 ;
;
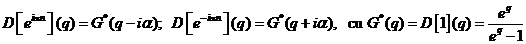 .
.
Prin
urmare:
 ;
;
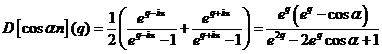 .
.
- Teorema de
derivare in raport cu un parametru
Daca f(n,x)  , atunci
, atunci 
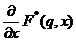 .
.
- Teorema de
derivare a imaginii (a transformatei Laplace discrete)
Daca f(n) 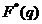 , atunci
, atunci 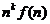
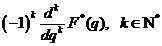 .
.
Exemplu
pentru teorema de derivare a transformatei Laplace
discrete
Sa calculam
transformata Laplace discreta a functiei
original disctreta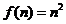 .
.
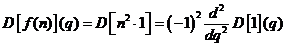 , conform teoremei de derivare a imaginii.
, conform teoremei de derivare a imaginii.
Dar 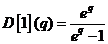 si prin urmare
rezulta:
si prin urmare
rezulta:
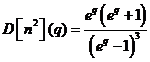 .
.
- Teorema de
integrare a transformatei Laplace discrete
Daca f(n)  , atunci
, atunci 
 .
.
- Transformata
Laplace discreta a diferentelor divizate de ordin k ale originalului
Daca f(n) 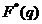 , atunci
, atunci 
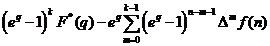 .
.
Definitia
diferentelor divizate de
ordin k
Fiind data  , diferentele divizate asociate lui f se definesc
recursiv, astfel:
, diferentele divizate asociate lui f se definesc
recursiv, astfel:
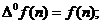
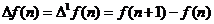 ;
;
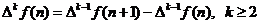 .
.
Observatie:
 .
.
- Transformata
Laplace discreta pentru o suma finita de functii original
Daca f(n) 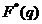 , atunci g(n)
, atunci g(n) 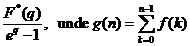 .
.
- Teorema
inmultirii (transformata Laplace discreta a produsului de convolutie)
Daca f(n) 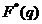 si g(n)
si g(n)  , atunci
, atunci 
 .
.
Definitia
produsului de convolutie (discret)
Daca  , atunci produsul lor de convolutie, notat
, atunci produsul lor de convolutie, notat  , este dat de:
, este dat de:
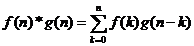 .
.
Folosind regulile de calcul de mai
sus, se pot deduce si se poate intocmi o lista de transformate Laplace discrete
folosite des in aplicatii.
Lista de transformate Laplace discrete
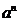
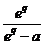 ;
; 
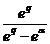 ;
;

 ;
; 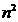
 ;
;
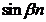
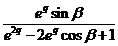 ;
; 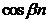
 ;
;
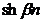
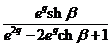 ;
; 
 ;
;
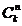
 ;
; 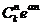
 ;
;

 .
.


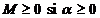 , atunci F(z) defineste o functie olomorfa in
domeniul
, atunci F(z) defineste o functie olomorfa in
domeniul 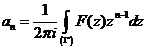 , unde
, unde  ,
, .
. .
.
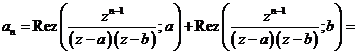
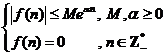 , atunci f se numeste functie original discreta.
, atunci f se numeste functie original discreta.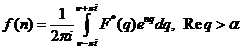 .
. ;
;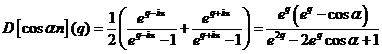 .
.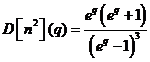 .
. .
. ;
;  ;
; ;
; ;
; ;
;  ;
; .
.