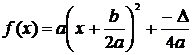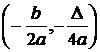 |  |
|
Ecuatii de gradul al doilea
ax2 + bx + c = 0, a,b,cIR, a 0
1. Formule de rezolvare D > 0
, 
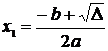, D = b2 - 4ac;
2. Formule utile in studiul ecuatiei de gradul al II-lea:
x12 + x22 = (x1 + x2)2 - 2x1x2 = S2 - 2P
x13 + x23 = (x1 + x2)3 - 3x1x2(x1 + x2) = S3 - 2SP
x14 + x24 = (x1 + x2)4 - 2x12x22= S4 - 4S2P + 2P2
3. Semnul functiei f:R R, f(x) = ax2 + bx + c, a,b,cIR
D > 0: a 0, x1 < x2.
|
x |
x1x2 + |
|
f(x) |
semnul lui a 0 semn contrar lui a 0semnul lui a |
D = 0
|
X |
x1 = x2 + |
|
f(x) |
semnul lui a 0 semnul lui a |
D < 0
|
X |
+ |
|
f(x) |
semnul lui a |
4. Graficul functiei f:R R, f(x) = ax2 + bx + c, a,b,cIR este o parabola.
Aceasta functie se poate scrie si sub forma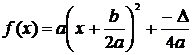 
, numita forma canonica.
Varful parabolei: V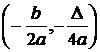
Maximul sau minimul functiei de gradul al doilea
1.
Daca
a > 0, functia f(x) = ax2 + bx + c are un minim egal cu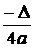 
, minim ce se realizeaza pentru x =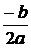 
2. Daca
a < 0, functia f(x) = ax2 + bx + c are un maxim egal cu 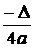, maxim ce se realizeaza pentru x =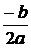
Descompunerea trinomului f(x) = aX2 + bX + c, a,b,cIR, a 0, x1 si x2 fiind radacinile trinomului.
1. D > 0, f(x) = a(X - x1)(X - x2);
2. D = 0, f(x) = a(X - x1)2;
3. D < 0, f(x) este ireductibil pe R, deci f(x) = aX2 + bX + c
Construirea unei ecuatii de gradul al doilea cand se cunosc suma si produsul radacinilor ei: x2 - Sx + P = 0, cu S = x1 + x2 si P = x1x2.
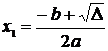Acest document nu se poate descarca
| E posibil sa te intereseze alte documente despre:
|
| Copyright © 2025 - Toate drepturile rezervate QReferat.com | Folositi documentele afisate ca sursa de inspiratie. Va recomandam sa nu copiati textul, ci sa compuneti propriul document pe baza informatiilor de pe site. { Home } { Contact } { Termeni si conditii } |
Documente similare:
|
Cauta document |