Analiza termenelor posibile - PROIECT

Timpul total cerut de indeplinirea unui grup de activitati depinde de:

Durata: cat tine fiecare activitate in parte;

Succesiune: ordinea in care se indeplinesc activitatile.

Exemplu: un proiect se compune din 10 activitati fiecare necesitand o saptamana pentru realizarea sa. Cat ar lua realizarea proiectuli? Nu se poate spune. Proiectul ar putea fi terminat intr-o saptamana daca se pot efectua toate activitatile concomitent si sunt suficiente resurse. Sau proiectul poate dura 10 saptamani daca activitatile sunt succesive. Sau proiectul poate lua intre una si 10 saptamani daca se pot face cateva activitati in paralel si cateva succesive.

Luati in considerare durata activitatilor si interdependentele cand realizati o lista (de activitati) pentru un proiect mic. Pentru proiecte cu mai mult de 15 - 20 de activitati, din care unele pot fi facute concomitent, aveti nevoie de o metoda care sa va ghideze in analiza.

1 Desenarea diagramelor retea

Diagrama retea este un grafic care ilustreaza ordinea in care se indeplinesc activitatile in proiect. Ganditi-va la diagrama retea ca la un test de laborator: va da o sansa sa sustineti diferite strategii chiar inaintea executarii lucrarii.

Diagrama retea include trei elemente:

Evenimentul - o intamplare semnificativa in viata proiectului dumneavoastra: cateodata numita "jalon" sau "reper". Evenimentul nu necesita timp si nu consuma resurse; el se intampla instantaneu. Ganditi-va la el ca la indicatoarele de directie ce inseamna ca ati ajuns la un anume punct in "drumul" spre terminarea proiectului. Evenimentul marcheaza startul sau finalul unei activitati sau a unui grup de activitati. Exemple de evenimente sunt: "aprobarea schitei" si "start realizare dosar prezentare".

Activitatea - operatiune necesara pentru a trece de la un eveniment la urmatorul din proiect. Activitatile necesita timp, consuma resurse si sunt descrise de verbe de actiune. Exemple de activitati: "schitare raport" si "turnat fundatie".

Durata: - timpul necesar pentru a finaliza o activitate. Cantitatea de efort ceruta, disponibilitatea oamenilor si faptul ca doi sau mai multi oameni pot munci la aceeasi activitate in acelasi timp influenteaza durata in timp. Capacitatea (de exemplu viteza de procesare a calculatorului si paginile scoase pe minut de un fotocopiator) si disponibilitatea resurselor nesalariale afecteaza de asemenea durata. Cunoscand fundamentul duratei va ajuta sa intelegeti caile de reducere a acesteia daca este necesar.

Exemplu. Un comerciant livreaza cereale cu un camion. Cu 8 ore de lucru pe zi ii trebuie 3 zile pentru finalizarea livrarii. Daca vrea sa scurteze durata la 2 zile, dublarea soferilor nu este suficienta, dar lucrand 12 ore pe zi va reusi. Unitatile de timp sunt folosite sa descrie doua caracteristici inrudite ale activitatilor. Durata in timp arata durata; efortul de munca este numarul total de ore munca pentru a termina sau indeplini o activitate.

Daca 4 oameni lucreaza 5 zile pentru a termina o activitate, durata activitatii este de 5 zile. Efortul de munca este 20 zile-om (4 persoane x 5 zile).

Se poate adauga o perioada pentru asteptare. Daca seful trebuie sa aprobe proiectul, il puneti in mapa unde sta 4 zile si sapte ore. Apoi seful il ia, il citeste intr-o ora si il semneaza. Durata activitatii este de 5 zile, efortul este de o ora.

Nu conteaza complexitatea proiectului, diagrama retea este formata din cele trei elemente.

2 Forme de diagrame retea

Puteti schita diagramele retea intr-una din cele doua forme:

Activitate tinta: numita si abordarea clasica sau traditionala;

Activitate in asteptare: numita si abordarea activitate incipienta.

Aceste doua forme sunt interschimbabile: orice activitate poate fi reprezentata in oricare dintre diagrame, diferenta constand in simbolurile folosite sa reprezinte cele trei elemente. Alte denumiri pentru diagrama:

Diagrama prioritara: termen pentru diagrama retea in abordarea activitate in asteptare;

Diagrama dependenta: termen pentru diagrama retea in orice format;

Grafic PERT: se refera la o diagrama retea in formatul activitate tinta.

PERT este acronimul pentru Programul de Evaluare si Revizie Tehnica. PERT a fost creat in 1950 pentru a planifica design-ul sistemului de arme Polaris. PERT este o tehnica de analiza care permite sa stabiliti optimist, pesimist si probabil durata activitatii, cand nu va asteptati ca realizarea activitatii va dura la fel dupa conditiile de mediu. Aceasta tehnica foloseste teoria probabilitatii pentru a determina posibilitatea de incadrare in timp a activitatilor individuale si in general posibilitatea ca durata proiectului se va incadra in limitele precizate.

Folosirea diagramei in format activitate tinta

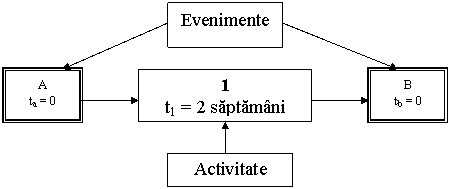
Abordarea activitate tinta foloseste simboluri distincte pentru a descrie fiecare din cele trei elemente ale diagramei:

un patrulater reprezinta un eveniment;

o linie cu sageata reprezinta o activitate;

litera "t" reprezinta perioada de timp.

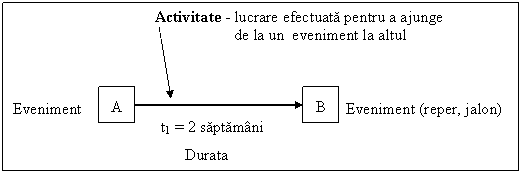
Fiecare activitate incepe si se termina cu un eveniment. Figura 4.1 reprezinta un exemplu simplu. Cand ajungeti la Evenimentul A (reprezentat prin careul din stanga) puteti desfasura activitatea (reprezentata prin sageata). Estimati ca activitatea va dura 2 saptamani pentru desfasurare (descrisa de nota t). Dupa terminarea activitatii, ajungeti la evenimentul B, reprezentat de careul din dreapta.

Figura 4.1 Simbolurile folosite in diagrama retea de tip activitate tinta

Surprinzator poate, lungimea sagetii reprezentand activitatea nu este proportionala cu durata activitatii.

Ocazional un al patrulea simbol este folosit in schema diagramei retea, si anume activitatea falsa care este o activitate cu durata zero, folosita sa reprezinte dependenta intre evenimente. Presupunem ca Marinescu si Multescu trebuie sa aprobe fiecare planul proiectului inainte sa incepeti implementarea lui. Reprezentati asta in diagrama retea cu doua evenimente separate: "Primirea aprobarii lui Marinescu" si "Primirea aprobarii lui Multescu" si aveti o activitate falsa pentru evenimentul "Planul proiectului terminat".

Folosirea diagramei in format activitate in asteptare

Abordarea activitate "in asteptare" foloseste doar doua simboluri sa descrie cele trei elemente ale diagramei:

un dreptunghi reprezinta atat evenimentul cat si activitatea; diferenta dintre eveniment sau activitate este durata: daca este zero, este eveniment. In plus casetele reprezentand evenimente, pot fi scoase in evidenta prin ingrosare, dublandu-se liniile lor sau sunt puse in prim plan.

litera "t" reprezinta perioada de timp.

O ilustrare simpla este cea din figura 4.2. Cand ajungeti la evenimentul A (dreptunghiul din stanga) puteti desfasura activitatea 1 (dreptunghiul din mijloc). Dupa terminarea Activitatii 1 ajungeti la evenimentul B (dreptungiul din dreapta).

Figura 4.2. Simbolurile folosite in diagrama de tip activitate in asteptare

Figura 4.2. ilustreaza folosirea abordarii activitatii "in asteptare" pentru a reprezenta evenimentele si activitatile; folosirea evenimentelor este optionala, o activitate putand conduce direct la urmatoarea fara un eveniment intre ele.

Alegerea unui format pentru diagrama retea

Cele doua forme ale diagramei sunt interschimbabile, nici o activitate nu poate fi reprezentata in una dintre diagrame fara a putea fi reprezentata in cealalta. Oricare ar fi formatul diagramei, luati in considerare urmatoarele:

Abordarea activitate tinta prezinta fiecare element cu un simbol unic. Aceasta ajuta daca tocmai ati invatat diagrama retea intrucat nu confundati activitatile si evenimentele;

Abordarea activitate in asteptare permite sa aranjati intregul proiect fara sa definiti nici un eveniment. Abordarea dureaza mai putin si ia mai putin spatiu pentru aranjat deoarece nu se cere sa definiti evenimentele;

Cele mai comune programe de gestiune a proiectului folosesc abordarea activitate in asteptare.

Vom folosi abordarea activitate in asteptare in continuare pentru ca este mai simpla de inteles, iar planurile sunt mai usor de integrat intr-un program software de management.

3 Analiza diagramei retea

Ganditi la proiect ca la o excursie cu prietenii. Fiecare are propria masina si calatoreste pe drumuri diferite. In timpul excursiei, rutele se intersecteaza in anumite locuri. Va intelegeti ca toti cei programati sa treaca printr-un punct comun, sosesc in acel punct si nu pleaca mai departe inainte ca ceilalti sa-si poata continua drumul. Excursia este gata cand toti ajung la destinatie.

O excursie atat de completa are nevoie de planificare pe harta pentru a determina cat timp dureaza intreaga excursie, a identifica dificultatile potentiale de-a lungul drumului si a analiza rutele alternative pentru acceasi destinatie.

Diagrama retea pentru acest proiect este harta. Fiecare etapa de voiaj reprezinta activitatile pe care membrii proiectului le vor desfasura, iar reperele reprezinta startul sau finalul etapei. O "cale" este succesiunea activitatilor desfasurate pe durata proiectului.

In desenarea si interpretarea diagramei retea se folosesc doua reguli:

Regula 1: dupa ce terminati o activitate sau ajungeti la un eveniment, puteti trece la activitatea sau evenimentul urmator asa cum este indicat prin sageata care pleaca de la activitatea sau evenimentul in cauza;

Regula 2: pentru a incepe o activitate sau a ajunge la un eveniment trebuie sa desfasurati toate activitatile si sa treceti prin toate evenimentele de la care vin sagetile care intra in evenimentul de la inceputul activitatii in cauza.

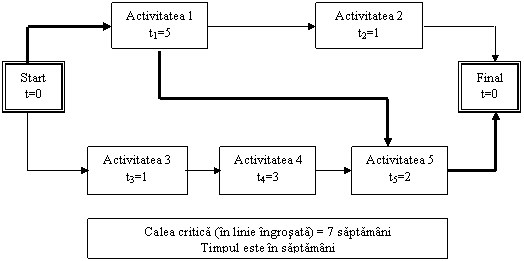
Figura 4.3. ilustreaza o diagrama retea schitata in formatul activitate in asteptare. Regula 1 spune ca dupa ce incepeti proiectul (atunci cand ajungeti la evenimentul "start") puteti desfasura Activitatea 1 sau 3 sau amandoua. Cu alte cuvinte activitatile 1 si 3 sunt independente una de alta.

De asemenea inseamna ca puteti sa nu faceti nici una din cele doua activitati. Regula 1 este o relatie "permisa" nu o relatie "fortata". Rezulta ca puteti lucra la activitatile ale caror sageti incep de la evenimentul "start", nu ca trebuie sa lucrati la una dintre ele. Daca insa nu lucrati la nici una, proiectul va intarzia.

Regula 2 spune ca puteti lucra la activitatea 2 imediat ce ati terminat activitatea 1 deoarece sageata de la activitatea 1 are o singura directie respectiv spre Activitatea 2. Regula 2 este o relatie "fortata". Daca sagetile de la trei activitati ar duce la activitatea 2, diagrama arata ca nu puteti incepe activitatea 2 daca nu finalizati toate cele trei activitati.

Figura 4.3 Exemplul unei diagrame retea.

Stabiliti urmatoarele informatii din diagrama retea pentru a intelege ce activitati sunt posibil de indeplinit si cum anume:

calea critica: o serie de activitati din proiect, aflate in succesiune, cu cea mai mare durata pentru a fi indeplinite impreuna;

calea necritica: o serie de activitati pe care le puteti amana catva timp si totusi sa terminati proiectul in cel mai scurt timp;

timp mort: perioada maxima de timp cu care puteti amana o activitate si totusi sa terminati proiectul in cel mai scurt timp;

cea mai apropiata data de debut: data cea mai apropiata la care puteti incepe o activitate;

cea mai apropiata data de final: data cea mai apropiata la care puteti incheia o activitate;

ultima data de incepere: ultima data cand puteti incepe o activitate si sa terminati proiectul in cel mai scurt timp posibil;

ultima data de final: ultima data cand puteti finaliza o activitate si sa terminati proiectul in cel mai scurt timp posibil.

Lungimea caii critice a proiectului determina cat timp va lua sa terminati proiectul. Daca vreti sa terminati proiectul intr-o perioada mai scurta, luati in considerare caile de scurtare a duratei activitatilor de pe calea critica. Monitorizati indeaproape activitatile de pe calea critica la realizarea proiectului; orice intarziere in desfasurarea activitatilor de pe calea critica va intarzia finalizarea proiectului.

Proiectul poate avea mai multe cai critice concomitent. De fapt fiecare cale din proiect poate fi critica daca va dura la fel pentru realizare. Aceasta este o situatie de risc ridicat deoarece intarzierea oricarei activitati duce imediat la intarzierea finalizarii proiectului.

Caile critice pot schimba desfasurarea proiectului. Cateva activitati situate pe calea critica sunt terminate mai devreme si astfel timpul total de terminare a caii critice devine mai mic decat cel cerut pentru terminarea unei cai necritice, acestea devenind cale critica. Este posibil, de asemenea ca activitatile unei cai initial necritica sa fie atat de intarziate incat sa devina cale critica.

"Pasul progresiv"- determinarea cailor critice, necritice si a celor mai apropiate datelor de incepere si finalizare a proiectului.

Primul pas in analiza diagramei retea este sa porniti de la inceputul proiectului sa vedeti cat de repede puteti desfasura activitatile de-a lungul fiecarei cai a proiectului pana cand ajungeti la finalul proiectului. Aceasta analiza inceput - sfarsit este numita "pasul progresiv".

Puteti parcurge in "pas progresiv" diagrama ilustrata in figura 4.3 astfel:

Regula 1 spune ca puteti incepe proiectul cu activitatea 1 sau 3 (cand ajungeti la evenimentul numit "Start"). In primul rand, luam in calcul calea superioara cuprinzand activitatile 1 si 2:

cel mai apropiat moment de incepere a activitatii este debutul proiectului;

cel mai repede puteti termina activitatea 1 la sfarsitul saptamanii a 5-a (se adauga estimarea duratei de 5 saptamani la cea mai timpurie data de incepere);

regula 2 spune ca cel mai devreme puteti incepe activitatea 2 la inceputul saptamanii a 6-a dupa finalizarea activitatii 1;

activitatea 2 poate fi terminata cel mai devreme la sfarsitul saptamanii 6.

Sa analizam calea de jos a diagramei ce cuprinde activitatile 3, 4 si 5:

cel mai devreme puteti incepe activitatea 3 la inceputul proiectului;

cel mai devreme puteti termina activitatea 3 la sfarsitul saptamanii 1;

cel mai devreme puteti incepe activitatea 4 la inceputul saptamanii a 2-a;

cel  mai devreme puteti termina activitatea 4 la sfarsitul saptamanii a 4-a;

Acum avem de-a face cu ceva diferit. Potrivit regulii 2 cele doua sageti care intra in Activitatea 5 arata ca nu puteti incepe activitatea 5 pana cand nu terminati Activitatea 1 si 4. Chiar daca terminati activitatea 4 la sfarsitul saptamanii 4 nu puteti termina activitatea 1 pana la sfarsitul saptamanii 5. Asadar, cel mai devreme puteti incepe activitatea 5 la inceputul saptamanii 6.

Aceasta situatie ilustreaza urmatoarea regula:

Daca doua sau mai multe activitati precedente conduc la aceeasi activitate, cea mai apropiata data de incepere a activitatii este cea mai tarzie data din datele de finalizare ale activitatilor precedente.

De exemplu, cea mai tarzie data pentru terminarea Activitatilor 4 si 1 este sfarsitul saptamanii 5. Asadar, cea mai apropiata data de incepere a Activitatii 5 este inceputul saptamanii 6.

Este greu? Lucrurile sunt complicate si pentru ca s-au folosit jocuri de cuvinte greu de urmarit.

cel mai devreme puteti incepe activitatea 5 la inceputul saptamanii 6;

cel mai devreme puteti finaliza activitatea 5 la sfarsitul saptamanii 7;

cel mai devreme puteti finaliza activitatea 2 la sfarsitul saptamanii 6;

Asadar, cel mai devreme puteti termina intregul proiect (sa ajungeti la evenimentul "Final") la sfarsitul saptamanii 7.

Pana acum ati aflat urmatoarele informatii despre proiect:

lungimea caii critice este de 7 saptamani, acesta fiind cel mai scurt timp in care proiectul poate fi terminat. Exista o cale critica care dureaza 7 saptamani: ea include evenimentul "Start", activitatea 1, activitatea 5 si evenimentul "Final";

activitatile 2, 3 si 4 nu sunt situate pe calea critica;

cele mai timpurii date la care puteti incepe si sfarsi fiecare activitate din proiect sunt trecute in Tabelul

Tabelul 4.1: Cele mai apropiate date pentru inceputul si sfarsitul activitatilor pentru Figura 4.3

"Pasul inapoi (revizuirea)" - determinarea timpilor morti, a datei celui mai apropiat inceput si a datei celui mai apropiat sfarsit

Sunteti la jumatatea drumului. Acum, este necesar sa determinati cat de mult puteti intarzia (amana) activitatile de-a lungul fiecarui cai (piste) a proiectului si totusi sa-l terminati cat mai devreme posibil. Aceasta analiza "de la coada la cap" se numeste revizuire (sau pasul inapoi).

Ati aflat din analiza precedenta ca cea mai apropiata data la care puteti ajunge la evenimentul "Final" este sfarsitul saptamanii 7. Totusi, regula 2 spune ca nu puteti ajunge la "Final" pana cand activitatile 2 si 5 nu sunt terminate. De aceea, daca vreti sa incheiati proiectul pana la sfarsitul saptamanii 7, cel mai tarziu cand puteti termina activitatile 2 si 5 este sfarsitul saptamanii 7. Tineti seama ca pista inferioara cuprinde activitatile 3,4 si 5.

v    trebuie sa incepeti activitatea 5 la inceputul saptamanii 6, cel mai tarziu, daca vreti sa terminati la sfarsitul saptamanii 7;

v    regula 2 spune ca nu puteti incepe activitatea 5 pana cand nu terminati activitatile 1 si 4. Deci, trebuie sa terminati activitatile 1 si 4 la sfarsitul saptamanii 5, cel tarziu;

v    trebuie deci sa incepeti activitatea 4 la sfarsitul saptamanii 3, cel tarziu;

v    trebuie sa terminati activitatea 3 inainte ca sa puteti lucra la activitatea 4. Deci, trebuie sa terminati activitatea 3 la sfarsitul saptamanii 2, cel tarziu;

v    trebuie sa incepeti activitatea 3 la inceputul saptamanii 2, cel tarziu;

Sa analizam pista superioara:

v    trebuie sa incepeti activitatea 2 la inceputul saptamanii 7, cel tarziu;

v    Nu puteti lucra la activitatea 2 pana cand nu terminati activitatea 1. De aceea, trebuie sa terminati activitatea 1 la sfarsitul saptamanii 6, cel tarziu;

Din nou, se observa o mica diferenta. Trebuie sa terminati activitatea 1 la sfarsitul saptamanii 5 pentru a permite lucrul la activitatea 5 pornita la inceputul saptamanii 6 si la sfarsitul saptamanii 6 sa permiteti munca la activitatea 2 ce va incepe la inceputul saptamanii 7. Terminand activitatea 1 la sfarsitul saptamanii 5, veti satisface ambele cerinte. Aceasta situatie ilustreaza urmatoarele:

v    Daca doua sau mai multe sageti pleaca de la aceeasi activitate sau eveniment, cea mai tarzie data la care trebuie sa terminati activitatea sau sa ajungeti la eveniment este cea mai tarzie data la care trebuie sa incepeti activitatea sau sa ajungeti la evenimentul catre care duc aceste sageti.

In acest exemplu, cea mai tarzie data pentru inceperea activitatilor 2 si 5 este inceputul saptamanii 7 si respectiv, inceputul saptamanii 6. Deci, cea mai tarzie data la care trebuie sa terminati activitatea 1 este sfarsitul saptamanii 5. Restul este simplu: trebuie sa incepeti activitatea 1 la inceputul saptamanii 1, cel mai tarziu.

Uneori simtiti ca v-ati pierdut in calcule. Daca se scrie cea mai apropiata si cea mai tarzie data pentru inceput (CMAI, CMTI) si cea mai apropiata si cea mai tarzie data pentru sfarsit (CMAS,CMTS) deasupra activitatilor, intregul proces se vede mai simplu, ca in figura 4.4.

Tabelul 4.2 Datele celui mai tarziu inceput si celui mai tarziu sfarsit pentru activitatile din figura 4.3.

Figura 4.4. Diagrama retea cu datele celui mai apropiat si celui mai tarziu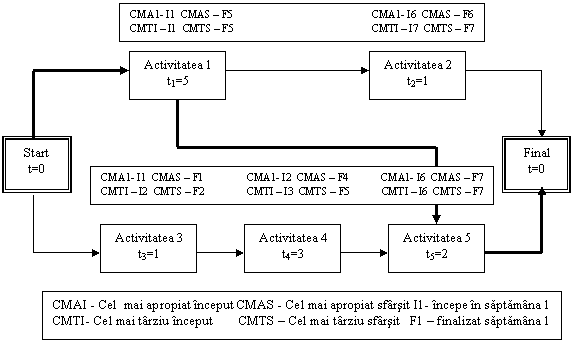
inceput si sfarsit.

Timpul mort asociat cu fiecare activitate se determina in doua moduri:

v    scadem data celui mai devreme inceput posibil din data celui mai tarziu inceput permis;

v    scadem data celui mai devreme final posibil din data celui mai tarziu final permis.

Tabelul 4.3 prezinta timpii morti pentru fiecare activitate. Daca timpul mort al unei activitati este zero activitatea este pe calea critica.

Tabelul 4.3 Timpii morti pentru diagrama retea din Figura 4.3.

Timpul mort este mai degraba asociat cu o secventa de activitatii decat cu o activitate individuala. Tabelul 4.3. indica faptul ca activitatile 2 si 3, situate pe aceeasi cale, au timpi morti cate o saptamana. Totusi, daca activitatea 2 este amanata cu o saptamana, activitatea 3 va avea timpul mort zero.

Corelatii intre activitati in diagrama retea

Pentru a schita diagrama retea a proiectului, trebuie sa decideti ordinea in care veti realiza activitatile proiectului.

Precursorul activitatii X este activitatea ce trebuie terminata inainte sa puteti lucra la activitatea X. O activitatea este un precursor imediat al activitatii X daca intre sfarsitul ei si inceputul activitatii X nu este nici o alta activitate.

Determinati "precursorul imediat" pentru fiecare activitate si dispuneti de toate informatiile necesare pentru a desena diagrama retea a proiectului.

Legaturile dintre activitati se pot baza pe cateva aprecieri:

- legaturi necesare: relatiile care trebuie sa fie observate daca activitatile proiectului sunt indeplinite cu succes.

Cerinte legale: legile sau normele europene, statale sau locale care impun anumite activitati obligatorii. De exemplu, un producator de pesticide, inainte de a incepe productia unui produs testat, este obligat de lege sa obtina mai intai aprobarea autoritatilor pentru noul produs.

Cerinte procedurale: procedurile interne care cer ca anumite activitati sa fie facute inaintea altora. Daca lansati un program de formare, dupa realizarea planului de formare este necesar ca acesta sa fie supus aprobarii interne, inainte de a cere aprobarea autoritatilor externe.

- legaturi discretionare: relatiile alese intre anumite activitati.

legaturi logice: cerinte logice cer sa faceti unele activitati inaintea altora, asa credeti ca are sens. Daca scrieti un raport in care capitolul 3 depinde in buna masura de capitolul 2, decideti sa scrieti capitolul 2 mai intai. Puteti lucra la capitolul 3 inainte sau puteti lucra la ambele capitole in acelasi timp, dar creste sansa ca sa refaceti capitolul 3, dupa ce terminati capitolul 2.

alegeri manageriale: acestea sunt decizii arbitrare de a lucra la anumite activitati inaintea altora, poate pentru ca ele sunt mai dificile, mai complexe, s.a.m.d;

Precursorul imediat al activitatilor proiectului se poate stabili astfel:

v    De la cap la coada:

alegeti activitatea(tile) ce le veti indeplini dupa debutul proiectului;

se tine seama de una din aceste activitati si se decide care activitate sau activitati le veti indeplini de indata ce veti termina activitatea aleasa;

se continua in acest fel pentru toate activitatile proiectului;

v    De la coada la cap:

se identifica ultima activitate sau ultimele activitati pe care le veti indeplini inainte ca proiectul sa fie gata;

se alege una din aceste activitati si se decide ce activitati veti indeplini imediat inaintea inceperii activitatii alese;

se continua in aceeasi maniera pana cand veti cuprinde toate activitatile din proiect.

In ambele cazuri, se noteaza precursorul imediat al ctivitatilor proiectului intr-un tabel simplu (tabelul 4.4).

Tabelul 4.4. Precursorul imediat al activitatilor din diagrama retea (figura 4.3)

Determinati prioritatea avand la baza natura si cerintele activitatilor si nu resursele care credeti ca vor fi disponibile. Sa presupunem ca Activitatile A si B pot fi facute in acelasi timp; totusi va imaginati ca veti desemna aceeasi persoana ca sa le faca pe amandoua. Stabiliti A precursor imediat pentru B, deoarece persoana poate lucra doar la o singura activitate la un moment dat. Pentru proiecte simple, puteti crea diagrama retea folosind linii pentru reprezentarea activitatilor si evenimentelor pe poster sau direct pe pereti. Pentru proiecte mai complexe, se foloseste programul de management al proiectelor.

5 Analiza unui exemplu simplu folosind diagrama retea

Se considera exemplul de pregatire a unui picnic pentru a demonstra cum puteti utiliza diagrama retea pentru a determina lista posibilitatilor si modalitatile de satisfacere a dorintelor oamenilor.

Exemplu: este vineri seara dupa o saptamana grea. Impreuna cu prietenul va ganditi ce puteti face in acest week-end pentru relaxare. Prognoza timpului pentru sambata este vreme insorita si linistita si decideti ca ati putea vizita un lac din apropiere pentru un picnic la lac. Hotarati sa planificati aceasta iesire cu grija, schitand si analizand diagrama retea.

Tabelul 4.5. arata 7 activitati identificate pentru a pregati picnicul de la lac.

In plus, sunteti de acord cu urmatoarele obligatii:

v    incepeti toate activitatile acasa, sambata dimineata la ora 8⁰⁰. Nu puteti face nimic inainte;

v    trebuie sa terminati activitatile inainte ca proiectul sa fie facut;

v    nu puteti schimba modul in care trebuie facute diferitele activitati;

v    daca doua lacuri sunt in directii opuse fata de casa, trebuie sa hotarati ce lac veti vizita inainte de a incepe sa conduceti masina.

Mai intai, decideti ordinea in care veti realiza activitatile. Cu alte cuvinte, determinati precursorul imediat pentru fiecare activitate.

Remarcam urmatoarele interdependente:

v    prietenul trebuie sa fiarba ouale inainte sa faca sandwich-urile cu oua;

v    amandoi trebuie sa decideti lacul inainte de a incepe sa rulati cu masina.

Tabelul 4.5. Activitati necesare pentru picnicul de la lac

Cum veti face restul activitatilor depinde de voi. Puteti lua in considerare urmatoarele modalitati:

v    de indata ce va veti decide asupra lacului, mergeti la banca pentru a lua banii;

v    dupa ce luati banii de la banca, cumparati benzina;

v    de indata ce veti decide lacul, prietenul incepe sa fiarba ouale;

v    Dupa ce ouale s-au fiert, prietenul face sandwich-urile;

v    de indata ce va intoarceti cu benzina si prietenul a terminat de facut sandwich-urile cu oua, incarcati masina;

v    Incepeti sa conduceti spre lac, imediat ce sunteti in masina;

Tabelul 4.6. Relatiile de precursor pentru activitatile definite.

Se schiteaza diagrama retea a proiectului, pornind de la informatiile din acest tabel, dupa cum urmeaza:

incepeti proiectul cu un evenimentul "Start";

apoi gasiti toate activitatile care nu au precursor imediat - ele pot fi pornite de indata ce incepeti proiectul; in acest caz, activitatea 5 este singura activitate de acest fel;

incepeti diagrama reprezentand aceste relatii. asa cum sunt ilustrate in figura 4.5.

Figura 4.5. Inceputul diagramei retea pentru picnicul de la lac

Reprezentati aceasta activitate intr-un dreptunghi si schitati o sageata de la evenimentul numit "Start" spre acest dreptunghi.

Gasiti toate activitatile care au activitatea 5 ca precursor imediat.

Tabelul arata ca sunt doua, activitatile 2 si 7. Reprezentati-le pe acestea cu dreptunghiuri si desenati sageti de la activitatea 5 spre aceste dreptunghiuri.

Continuati in acelasi mod.

Se observa ca activitatea 6 este singura activitate care are activitatea 2 ca precursor imediat. Desenati un dreptunghi reprezentand activitatea 6 si schitati o sageata de la activitatea 2 la activitatea 6. La fel, pe ramura de jos, desenati un dreptunghi reprezentand activitatea 3 si schitati o sageata de la activitatea 7 la activitatea 3. Diagrama retea in constructie este ilustrata in figura 4.6.

Figura 4.6. Continuarea diagramei retea pentru picnicul de la lac

Acum realizati ca activitatea 1 are ca precursor imediat atat activitatea 3, cat si activitatea 6. Desenati un dreptunghi reprezentand activitatea 1 si schitati sageti de la activitatea 3 spre activitatea 1 si de la activitatea 6 spre activitatea 1.

Figura 4.7. Diagrama retea finala pentru picnicul de la lac in format "activitate tinta"

Restul este simplu. Activitatea 4 este singura activitate care are ca precursor imediat activitatea 1. De aceea, desenati un dreptunghi reprezentand activitatea 4 si schitati o sageata de la activitatea 1 la activitatea 4. In final, desenati un dreptunghi reprezentand evenimentul numit "Final". Figura 4.7. arata forma finala a diagramei retea a proiectului.

O intrebare importanta: Mai intai, cat timp dureaza sa ajungeti la lac?

v    Calea superioara, cu activitatile 2 si 6, necesita 15 minute pentru finalizare;

v    Calea inferioara, cu activitatile 7 si 3 ia 20 minute pentru a fi completa;

v    Deoarece drumul critic este cel mai lung drum de la un capat la celalalt al proiectului, calea cuprinzand activitatile 5, 7, 3, 1 si 4 este calea critica. Dureaza 57 minute pentru a ajunge la lac dupa planul din acesta diagrama;

Puteti amana (intarzia) una din activitati si totusi sa ajungeti la lac in 57 de minute? Care sunt aceste activitati?

v    Calea superioara cuprinzand activitatile 2 si 6 este o cale necritica;

v    Diagrama retea arata ca activitatile 5, 7, 3, 1 si 4 sunt pe calea critica si de aceea, nici una nu poate fi amanata daca vreti sa ajungeti la lac in 57 minute.

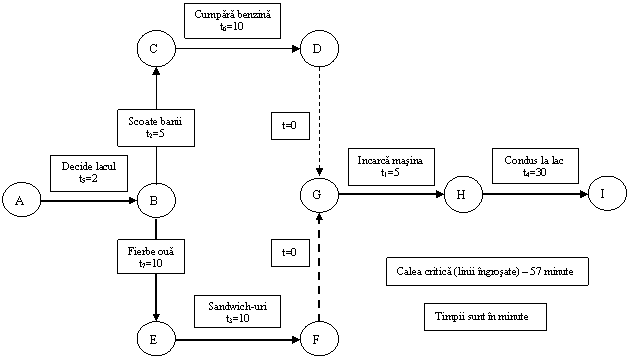
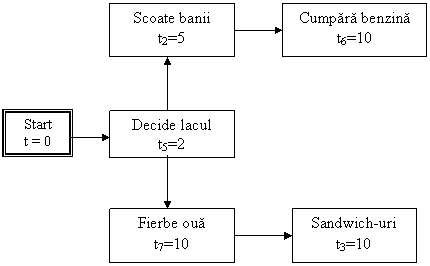
Figura 4.8. Diagrama retea finala "picnic la lac" in format "activitate in asteptare"

v    Cu toate acestea, activitatile 2 si 6 pot fi indeplinite in acelasi timp cu activitatile 7 si 3. Activitatile 7 si 3 necesita 20 minute pentru a le indeplini, in timp ce activitatile 2 si 6 doar 15 minute. Deci, activitatile 2 si 6 au 5 minute timp mort.

Figura 4.8. arata diagrama retea pentru acest proiect schitata intr-un format "activitate in asteptare". Evenimentul A este echivalentul "Start" (Pornire) si evenimentul I este echivalentul "Finalului" din figura 4.7.

S-au schitat evenimentele la inceputul si sfarsitul fiecarei activitati in figura 4.8., insa nu au fost inca denumite. Este posibil sa se tina seama de activitatea tocmai finalizata. De exemplu:

v    evenimentul B, finalul activitatii 5 "decide lacul" poate fi numit "decis lacul";

v    evenimentul C, finalul activitatii 2, "scoate banii" poate fi numit "bani obtinuti" si asa mai departe.

Un eveniment simplu este acela care reprezinta indeplinirea unei singure activitati. Definirea evenimentelor simple de la sfarsitul tuturor activitatilor in formatul 'activitate tinta', face proiectul mai usor de supravegheat si de raportat starea de indeplinire a activitatilor. Daca activitatea are precursori multiplii, in loc de a avea sageti pentru fiecare precursor venind direct in miezul evenimentului de la care pleaca activitatea X, se fac urmatoarele:

fiecare dintre precursori se termina intr-un singur eveniment;

se leaga toate evenimentele intr-unul prin activitati fictive;

astfel activitatea X pleaca de la un singur eveniment.

Aceasta tehnica este ilustrata in figura 4.8. Trebuie sa finalizati activitatea 6, 'Cumpara benzina', si prietenul trebuie sa finalizeze activitatea 3, 'Pregatit sandwich-uri', inainte sa incarcati masina. Decat sa aveti fiecare activitati care sa conduca la Evenimentul G, activitatea 6 se termina in Evenimentul D. 'Benzina cumparata', si activitatea 3 se termina in Evenimentul F, 'Sandwich-uri facute'. Dupa aceea se deseneaza activitati fictive de la evenimentele D si respectiv F la evenimentul G, care va fi definit 'gata de a incarca masina'.